目录
目录:
1:归并排序递归
2:归并排序的非递归
3:计数排序的思想
1:归并排序递归
思路:归并排序是采用分治算法的一种排序,将两个有序的子数组合并到一个数组中去使得数组完全有序,所以我们先使子数组有序,在使整体的数组有序,这种先让子数组有序,最后在使整体完全有序,也称为二路归并。
归并排序的核心步骤如下图:
思路:先将数组划分为两个区间,使得左右两个区间有序 ,在借用tmp数组将两个有序的区间合并成一个有序的区间,最后在将tmp数组中的值拷贝到原数组中去,而要使左右区间有序,那么我们又得将左右区间划分为两个部分,使得左右区间的子区间变成有序,在利用tmp数组来进行归并.......,这个过程肯定涉及递归与合并的过程,最后归并的过程是左右子区间都有序,即区间数为1的时候,就得开始归并了。这个思路需要自行去画图来感悟,才能有更好的理解。
如下图:
代码如下:
void _MergeSort(int* a, int* tmp, int begin, int end)
{
//递归返回条件
if (begin >= end)
return;
//将区间分为左右两个子区间
int mid = (begin + end) / 2;
//递归左边
_MergeSort(a, tmp, begin, mid);
_MergeSort(a, tmp, mid + 1, end);
//走到这里,说明我们得开始合并两个子数组了
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int index = begin;//要保证index在tmp数组中同一个位置
while (begin1 <= end1 && begin2 <= end2)
{
//取小的尾插
if (a[begin1] > a[begin2])
{
tmp[index++] = a[begin2++];
}
else
{
tmp[index++] = a[begin1++];
}
}
//肯定有一个区间没有完全插入到tmp数组
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//拷贝回原数组 区间为左闭右闭所以还得加1,拷贝空间的个数
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
_MergeSort(a, tmp, 0, n - 1);
}归并排序的时间复杂度为标准的O(N*logN),因为每一层都有n个数需要合并,一共有高度层。
空间复杂度:O(N),开了一块临时的空间,在该空间上进行插入。
2:归并排序的非递归
我们先上代码吧!!
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail:");
return;
}
//归并的数据个数
int gap = 1;
//数组中每一组都得归并
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//[begin1,end1]与[begin2,end2]一起进行归并
int index = i;
if (end1 >= n || begin2 >= n)
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] >= a[begin2])
{
tmp[index++] = a[begin2++];
}
else
{
tmp[index++] = a[begin1++];
}
}
//有一个未尾插完
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * (end2-i+1));
}
gap *= 2;
}
}归并排序递归的思路:要想整体有序就得左右子区间先有序,一次递归下去。
非递归的思路:直接先从11开始归并,然后22归并,44归并,一直以两倍进行归并下去。

在上图采用非递归进行归并的时候,我们需要注意的就是4这个数字,当我们将数组划分为
[begin1,end1],[begin2,end2]的时候,假如我们的end1越界了,即end1>=n或begin2越界,我们就不需要对他进行归并,直接break跳出循环就行了。
当只有end2越界的时候,这时需要先将end2的值改为n-1,然后在进行归并即可。
非递归形式下的时间与空间复杂度与递归一样。
3.计数排序
关于计数排序应该是在这些排序中思路最简单的排序了。
计数排序的思想是,统计原数组中值的个数,在另外一块空间中对应下标++,然后从下标为0开始遍历数组,当遍历到数组中的值不为0时,将该数尾插到原数组。
我们通过图来讲解
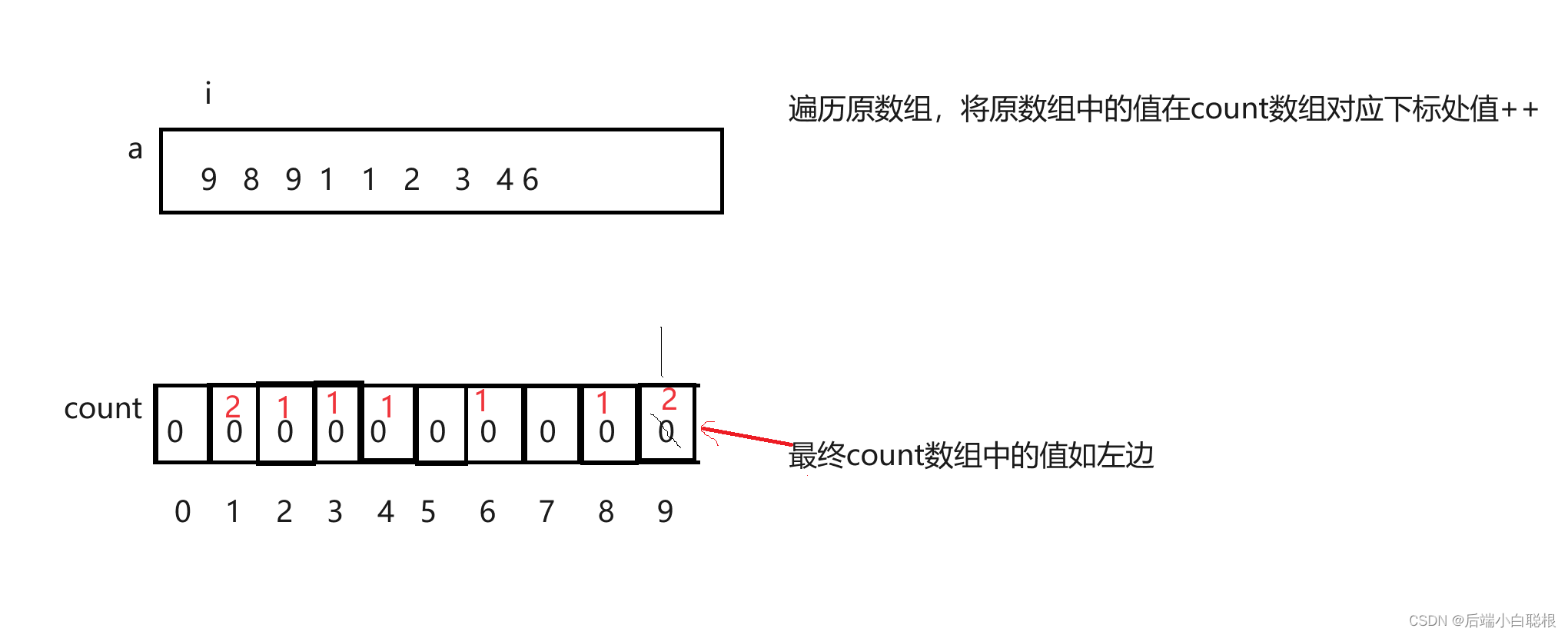
这种方式是采用了绝对映射的方式,即原数组中值出现,对应在count数组下标处进行++
而当数据非常大,但是也属于相对集中的范围,则我们需要采取相对映射的方式来进行。
相对映射是可以用来减少开辟空间的个数的。
图:
从这里我们也能看出来,计数排序的缺点:1.只能对相对集中的值进行排序,否则会浪费空间
代码如下:
void CountSort(int* a, int n)
{
int max = a[0];
int min = a[0];
//为相对映射做准备,统计数组中最大与最小值
for (int i = 0; i < n; i++)
{
if (a[i] > max)
{
max = a[i];
}
if (a[i] < min)
{
min = a[i];
}
}
//开辟range个空间,用来统计每个数出现的次数
int range = max - min + 1;
//在统计前一定要将count数组中值全部变为0,calloc默认初始化可以实现这一功能
int* count = (int*)calloc(range, sizeof(int));
//统计数组中元素的个数
for (int i = 0; i < n; i++)
{ //相对映射在a[i]-min处++
count[a[i] - min]++;
}
int index = 0;
for (int i = 0; i <= range; i++)
{
//进行最后的排序,并且将值回显
while (count[i] > 0)//统计k次
{
a[index++] = i + min;
count[i]--;
}
}
}时间复杂度:为O(N+range),N为数组的个数,range为映射开辟的空间
空间复杂度:O(range)
本章到这里在知识点就已经分享完毕了,感谢大家的耐心观看,如果你觉得有用的话可以给博主一个赞哦!!!