目录
1. 归并排序的原理
1.1 二路归并排序执行流程
2. 代码分析
2.1 代码设计
3. 性能分析
4. 非递归版本
1. 归并排序的原理
“归并”一词的中文含义就是合并、并入的意思,而在数据结构中的定义是将两个或者两个以上的有序表组合成一个新的有序表。
归并排序(Merging Sort)就是利用归并的思想实现的排序方法。它的原理是假设初始序列含有n个记录,则可以看成是n个有序的子序列,每个子序列的长度为1,然后两两归并,得到[n/2](表示不小于x的最小整数)个长度为2或1的有序子序列;再两两归并,……,如此重复,直至得到一个长度为n的有序序列为止,这种排序方法成为2路归并排序。
1.1 二路归并排序执行流程
原始序列:49 38 65 97 76 13 27
(1)将原始序列看成7个只含有一个关键字的子序列,显然这些子序列都是有序的。
子序列1:49;子序列2:38;子序列3:65;子序列4:97;子序列5:76;子序列6:13;子序列7:27
(2)两两归并,形成若干有序二元组,即49和38归并成{38 49},65和97归并成{65 97},76和13归并成{13 76},27没有归并对象,保持原样{27}。第一趟二路归并排序结束,结果如下:
{38 49},{65 97},{13 76},{27}
(3)再将这个序列看成若干二元组子序列
子序列1:38 49;子序列2:65 97;子序列3:13 76;子序列4:27;
最后一个子序列长度可能是1,也可能是2。
(4)继续两两归并,形成若干有序四元组(同样,最后的子序列中不一定有4个关键字),即{38 49}和{65 97}归并形成{38 49 65 97},{13 76}和{27}归并形成{13 27 76}。第二趟二路归并排序结束,结果如下:
{38 49 65 97},{13 27 76}
(5)最后只有两个子序列了,再进行一次归并,就可完成整个二路归并排序,结果如下:
13 27 38 49 65 76 97
2. 代码分析
大家先看看有没有思路!
3,2,1 开始我的表演哈哈哈!
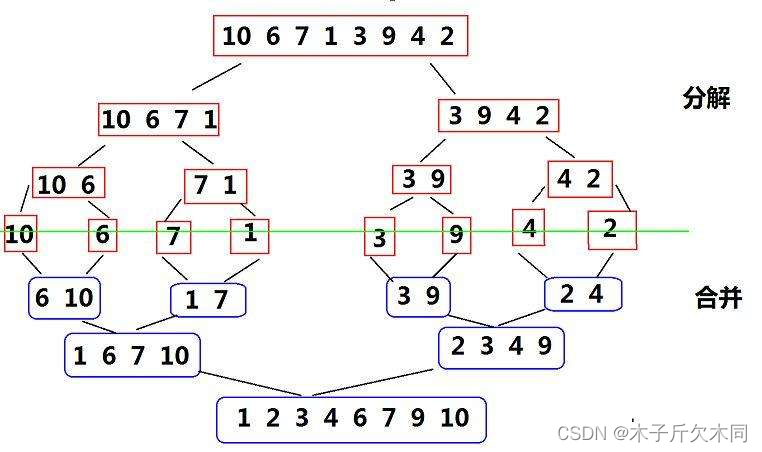
请看图解:

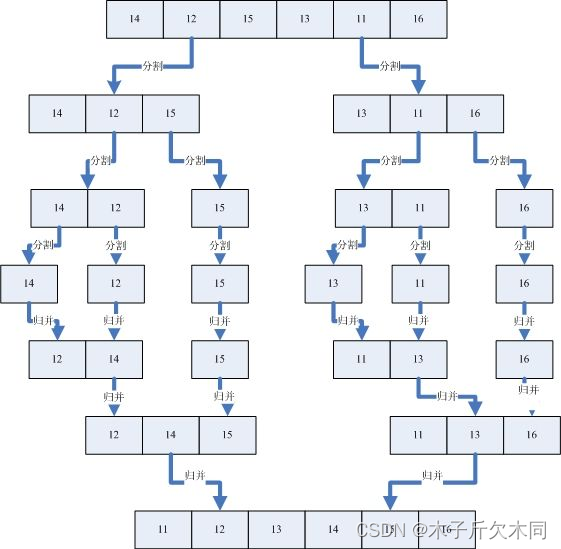
2.1 代码设计
根据图解我们要怎么设计方法呢?
我打算把分解功能写成一个方法,合并功能写成一个方法。具体实现如下:
public static void mergeSort1(int[] array){
mergeSortDivide(array,0, array.length - 1);
}
//分解
private static void mergeSortDivide(int[] array,int left,int right){
//终止条件:left > right
while(left >= right){
return;
}
int mid = (left+right)/2;
//递归左子序列
mergeSortDivide(array,left,mid);
//递归右子序列
mergeSortDivide(array,mid+1,right);
//合并
merge(array,left,right,mid);
}
//合并
private static void merge(int[] array,int start,int end,int mid){
//左子序列从start开始
int s1 = start;
//右子序列从mid+1开始
int s2 = mid + 1;
//新建一个数组,作为复制数组
int[] tmp = new int[end - start + 1];
//k表示中间数组的元素下标
int k = 0;
//开始比较
while(s1 <= mid && s2 <= end){
if(array[s1] <= array[s2]){
//将小的值赋值给tmp[k]
//小伙伴们这可以思考一下:为什么不能先写array[s2] <= array[s1]?
//等下看我下面的解析!
tmp[k++] = array[s1++];
} else{//array[s2] <= array[s1]的情况
tmp[k++] = array[s2++];
}
}
//有剩余的数组
//左子序列
while(s1 <= mid){
tmp[k++] = array[s1++];
}
//右子序列
while(s2 <= end){
tmp[k++] = array[s2++];
}
//将tmp数组的值赋值给array数组
for(int i = 0;i<tmp.length;i++){
array[i+start] = tmp[i];
}
}回答问题:为什么不能先写array[s2] <= array[s1]?
答:归并排序是稳定的。如果先写array[s2] <= array[s1],那么在s2开始的元素与s1开始的元素相等的话,例如:1<=1,那么本该在后面的1就会移到前面,导致这段代码实现的归并排序不稳定了!
3. 性能分析
| 时间复杂度 | 空间复杂度 |
| O(n*log(n)) | O(n) |

4. 非递归版本
上面的版本是递归版本,接下来是非递归版本。

private static void merge(int[] array,int start,int end,int mid) {
int s1 = start;
//int e1 = mid;
int s2 = mid+1;
//int e2 = end;
int[] tmp = new int[end-start+1];
int k = 0;//tmp数组的下标
while (s1 <= mid && s2 <= end) {
if(array[s1] <= array[s2]) {
tmp[k++] = array[s1++];
}else {
tmp[k++] = array[s2++];
}
}
while (s1 <= mid) {
tmp[k++] = array[s1++];
}
while (s2 <= end) {
tmp[k++] = array[s2++];
}
for (int i = 0; i < tmp.length; i++) {
array[i+start] = tmp[i];
}
}
public static void mergeSort(int[] array) {
int gap = 1;
while (gap < array.length) {
// i += gap * 2 当前gap组的时候,去排序下一组
for (int i = 0; i < array.length; i += gap * 2) {
int left = i;
int mid = left+gap-1;//有可能会越界
if(mid >= array.length) {
mid = array.length-1;
}
int right = mid+gap;//有可能会越界
if(right>= array.length) {
right = array.length-1;
}
merge(array,left,right,mid);
}
//当前为2组有序 下次变成4组有序
gap *= 2;
}
}