二叉排序树
基本介绍

二叉排序树创建和遍历

class Node:
"""
创建 Node 节点
"""
value: int = 0
left = None
right = None
def __init__(self, value: int):
self.value = value
def add(self, node):
"""
添加节点
node 表示要添加的节点
"""
if node is None:
return
# 判断要添加节点和当前子树根节点的大小
if node.value < self.value:
# 要添加节点小于当前子树根节点
if self.left is None:
# 如果当前子树左子节点为空,则直接将要添加的节点挂在左子节点上
self.left = node
else:
# 否则,递归当前子树的左节点,找到要放置的位置
self.left.add(node)
else: # 要添加节点大于等于当前子树根节点
if self.right is None:
# 如果当前子树右子节点为空,则直接将要添加的节点挂在右子节点上
self.right = node
else:
# 否则,递归当前子树的右节点,找到要放置的位置
self.right.add(node)
def infix_order(self):
"""
中序遍历二叉树
"""
if self.left:
self.left.infix_order()
print(self.value)
if self.right:
self.right.infix_order()
class BinarySortTree:
"""
二叉排序树
"""
root: Node = None
def add(self, node: Node):
"""
添加节点
node: 要添加的节点
"""
if self.root is None:
# 如果根节点为空,直接将新节点当做根节点
self.root = node
else:
# 否则,将新节点放在根节点下
self.root.add(node)
def infix_order(self):
"""
中序遍历
"""
if self.root:
self.root.infix_order()
else:
print("二叉排序树为空...")
arr = [7, 3, 10, 12, 5, 1, 9]
binary_sort_tree = BinarySortTree()
for i in arr:
node = Node(i)
binary_sort_tree.add(node)
binary_sort_tree.infix_order()二叉排序树的节点删除
思路分析

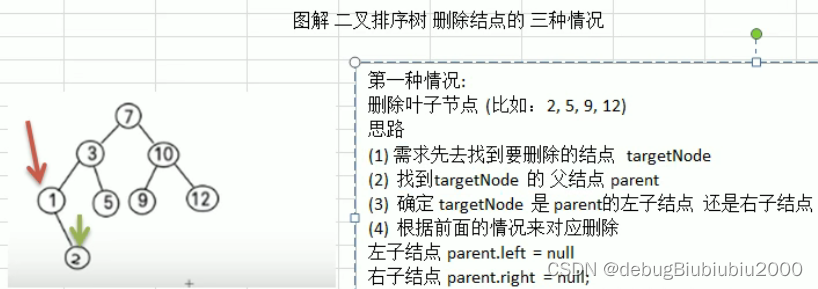

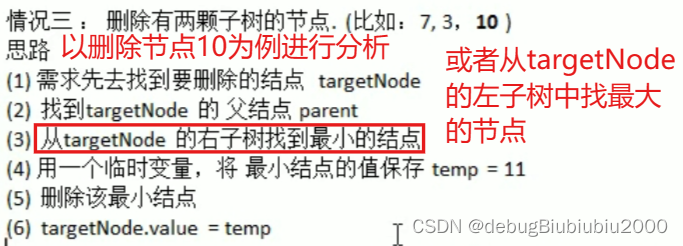
代码实现
"""二叉排序树"""
class Node:
"""
创建 Node 节点
"""
value: int = 0
left = None
right = None
def __init__(self, value: int):
self.value = value
def add(self, node):
"""
添加节点
node 表示要添加的节点
"""
if node is None:
return
# 判断要添加节点和当前子树根节点的大小
if node.value < self.value:
# 要添加节点小于当前子树根节点
if self.left is None:
# 如果当前子树左子节点为空,则直接将要添加的节点挂在左子节点上
self.left = node
else:
# 否则,递归当前子树的左节点,找到要放置的位置
self.left.add(node)
else: # 要添加节点大于等于当前子树根节点
if self.right is None:
# 如果当前子树右子节点为空,则直接将要添加的节点挂在右子节点上
self.right = node
else:
# 否则,递归当前子树的右节点,找到要放置的位置
self.right.add(node)
def infix_order(self):
"""
中序遍历二叉树
"""
if self.left:
self.left.infix_order()
print(self.value)
if self.right:
self.right.infix_order()
def search_delete(self, value: int):
"""
查找要删除的节点
:param value: 要删除节点的值
:return:
"""
if self.value == value: # 当前节点就是要找的删除的节点,返回
return self
elif value < self.value: # 要删除的值小于当前节点的值,则在当前节点的左子树递归查找
if self.left:
return self.left.search_delete(value)
return None
else: # 要删除的值大于当前节点的值,则在当前节点的右子树递归查找
if self.right:
return self.right.search_delete(value)
return None
def find_parent(self, value: int):
"""
查找要删除节点的父节点
:param value: 要删除的节点值
:return:
"""
if (self.left and self.left.value == value or
self.right and self.right.value == value):
return self
else:
# 如果要删除的值小于当前节点的值,且当前节点有左节点,则向左节点递归查找
if value < self.value and self.left:
return self.left.find_parent(value)
# 如果要删除的值大于等于当前节点的值,且当前节点有右节点,则向右 节点递归查找
elif value >= self.value and self.right:
return self.right.find_parent(value)
return None # 没有找到父节点,返回空,表示没有父节点,即要删除的是根节点
class BinarySortTree:
"""
二叉排序树
"""
root: Node = None
def add(self, node: Node):
"""
添加节点
node: 要添加的节点
"""
if self.root is None:
# 如果根节点为空,直接将新节点当做根节点
self.root = node
else:
# 否则,将新节点放在根节点下
self.root.add(node)
def infix_order(self):
"""
中序遍历
"""
if self.root:
self.root.infix_order()
else:
print("二叉排序树为空...")
def search_delete(self, value) -> Node:
"""
查找要删除的节点
:param value: 要删除节点的值
:return:
"""
if self.root:
return self.root.search_delete(value)
return None
def find_parent(self, value) -> Node:
"""
查找要删除节点的父节点
:param value: 要删除节点的值
:return:
"""
if self.root:
return self.root.find_parent(value)
return None
def find_and_delete_right_tree_min(self, node: Node) -> int:
"""
查找以 node 为根节点的二叉排序树的最小节点
返回小节点的值并从该二叉排序树中删除最小节点
:param node:
:return:
"""
t = node
while t.left: # 因为要找最小节点,所以从二叉排序树的左子树中找
t = t.left
# 退出循环时,t 指向的就是最小节点
val = t.value
self.delete_node(val)
return val
def delete_node(self, value: int):
"""
删除接地那
:param value: 要删除节点的值
:return:
"""
if self.root is None:
print("二叉树为空,不能删除节点...")
return
# 查找要删除的节点
target_node = self.search_delete(value)
if target_node is None: # 找不到要删除的节点
print(f"节点{value}不存在")
return
if self.root.left is None and self.root.right is None:
# 此时找到了要删除的节点,且二叉树只有一个节点,所以要删除的就是这唯一的一个节点
self.root = None
return
# 查找要删除节点的父节点
parent = self.find_parent(value)
if target_node.left is None and target_node.right is None:
# 此时说明要删除的节点是叶子节点
# 进一步判断要删除的节点是父节点的左节点还是右节点
if parent.left and parent.left.value == value:
# 说明要删除节点是父节点的左子节点
parent.left = None
return
if parent.right and parent.right.value == value:
# 说明要删除节点是父节点的右子节点
parent.right = None
return
elif target_node.left and target_node.right:
# 要删除的节点有左右两棵子树
# 从要删除节点的右子树中找到最小节点,获得该最小节点的值并删除该最小节点
# 然后将最小节点的值赋值给要删除节点
min_val = self.find_and_delete_right_tree_min(target_node.right)
target_node.value = min_val
# 同理,也可以从要删除节点的左子树找到最大节点,获得该最大节点的值并删除该最大节点
# 然后将最大节点的值赋值给要删除节点
else:
# 要删除的节点只有一棵子树
# 进一步确定要删除节点的子树是左子树还是右子树
if target_node.left:
# 要删除节点的子树是左子树
if parent is None:
# 如果父节点为空,说明要删除的是根节点,则直接让根基诶到哪等于它的左子节点
self.root = target_node.left
# 进一步判断要删除的节点是父节点的左节点还是右节点
elif parent.left.value == value:
# 要删除的节点是父节点的左节点
parent.left = target_node.left
else: # 要删除的节点是父节点的右节点
parent.right = target_node.left
else: # 要删除节点的子树是右子树
if parent is None:
# 如果父节点为空,说明要删除的是根节点,则直接让根基诶到哪等于它的右子节点
self.root = target_node.right
# 进一步判断要删除的节点是父节点的左节点还是右节点
elif parent.left.value == value:
# 要删除的节点是父节点的左节点
parent.left = target_node.right
else: # 要删除的节点是父节点的右节点
parent.right = target_node.right
# 测试二叉排序树的创建和遍历
arr = [7, 3, 10, 12, 5, 1, 9, 2]
binary_sort_tree = BinarySortTree()
for i in arr:
node = Node(i)
binary_sort_tree.add(node)
binary_sort_tree.infix_order()
# 测试删除二叉排序树的结点
binary_sort_tree.delete_node(7)
print("删除节点后:")
binary_sort_tree.infix_order()



![[Linux 基础] make、Makefile自动化构建代码工具](https://img-blog.csdnimg.cn/bba5604b7e2f4803b73acaee31e1793e.png)