二叉树的各类实现判断

news2024/10/3 20:21:08

如何判断一颗二叉树是否是搜索二叉树？ 

搜索二叉树

每个子树头节点的左孩子比它小，右孩子比它大

经典的搜索二叉树没有重复的数

判断

将二叉树按照中序遍历，判断是否为升序

1、先将整棵树中序遍历再判断是否升序
    //中序遍历
    public static ArrayList<Node> traverse_medium(Node node) {
        if (node == null) {
            return null;
        }

        ArrayList<Node> list = new ArrayList<>();

        traverse_medium(node.left);
        //输出改为存储入集合之中
        list.add(node);
        traverse_medium(node.right);

        return list;
    }

    //判断搜索二叉树
    public static boolean is_bst_one(ArrayList<Node> list) {
        for (int i = 0; i < list.size() - 2; i++) {
            if (list.get(i).value >= list.get(i + 1).value) {//这里认为等于不可行
                return false;
            }
        }
        return true;
    }
2、在中序遍历的过程中判断是否升序
        （1） 使用递归的中序遍历
    //判断搜索二叉树
    public static boolean is_bst_two1(Node node) {
        if (node == null) {
            return true;//认为空二叉树是搜索二叉树
        }

        int preValue = Integer.MIN_VALUE;

        //判断左子树是否为搜索二叉树
        boolean isLeftBst = is_bst_two1(node.left);

        //中序遍历的第二轮，输出改为判断
        //如果左树不是搜索二叉树，那么整棵树一定不是搜索二叉树
        if (!isLeftBst) {
            return false;
        }
        if (node.value > preValue) {
            preValue = node.value;//递归逐层向下找，会最先找到最左侧的节点，逐层向上比较，preValue逐层向上赋值
        } else {//node.value <= preValue，不满足搜索二叉树条件
            return false;
        }

        //在左子树为搜索二叉树的前提下，如果右子树为搜索二叉树，那么整棵树一定都是搜索二叉树
        return is_bst_two1(node.right);
    }
        （2）不使用递归的中序遍历 
    //判断搜索二叉树
    public static boolean is_bst_two2(Node node) {
        if (node == null) {
            return true;//认为空二叉树是搜索二叉树
        }

        int preValue = Integer.MIN_VALUE;

        Stack<Node> stack = new Stack<Node>();
        while (!stack.isEmpty() || node != null) {
            if (node != null) {
                stack.push(node);
                node = node.left;//整个左子树入栈
            } else {
                node = stack.pop();//出栈

                //输出变为比较
                if (node.value <= preValue) {//不满足条件
                    return false;
                } else {//node.value > preValue，满足条件
                    preValue = node.value;//preValue逐层向上
                }

                node = node.right;//如果右节点为null则弹出下一个，如果不为null则将右节点弹入栈
            }
        }
        return true;
    }

如何判断一颗二叉树是否是完全二叉树？ 

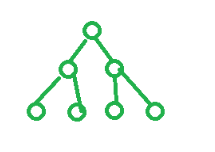
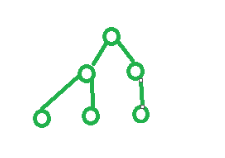
完全二叉树

二叉树从左向右依次变满（左图为满二叉树，右图为普通的完全二叉树）

          

判断

二叉树按宽度遍历

条件1：如果某一个子树的头节点有右孩子没有左孩子，返回false

条件2：在条件1的前提下，如果有一个节点左右孩子不双全，后续的节点都是叶节点（它右侧的所有节点都没有子节点）

    //判断完全二叉树
    public static boolean isCBT(Node node) {
        if (node == null) {
            return true;//空二叉树认为是完全二叉树
        }

        boolean notBoth = false;//记录是否遇到不双全的节点
        Node left = null;
        Node right = null;

        Queue<Node> queue = new LinkedList<>();
        queue.add(node);

        while (!queue.isEmpty()) {
            Node node0 = queue.poll();

            if ((left == null && right != null)//不满足条件1：左节点null且右节点不为null
                    || (notBoth && (left != null || right != null))) {//不满足条件2：遇到不双全的节点但后面的节点不为叶节点
                return false;
            }
            
            if (node0.left != null) {
                queue.add(node0.left);//先右节点入队列
            }
            if (node0.right != null) {
                queue.add(node0.right);//再左节点入队列
            }

            if (left == null || right == null) {//不双全的节点
                notBoth = true;
            }
        }
        return true;
    }

如何判断一颗二叉树是否是满二叉树？ 

满二叉树

相关题目

求二叉树的最大深度或节点个数

已知最大深度为max，则节点个数  N = 2^{^{max}} - 1

二叉树的递归套路判断是否为满二叉树

这里可以先看下面的递归套路再理解如何用套路求是否为满二叉树

递归套路：返回二叉树的最大深度，节点个数

在调用的函数中判断是否满足满二叉树的条件

package binarytree;

public class IsFullBinaryTree {

    public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int data) {
            this.value = data;
        }
    }


    public boolean isFullBinaryTree(Node node) {
        return process(node).nodeNumber == Math.pow(2,process(node).depth) - 1;//nodeNumber是否等于2的depth次方-1
    }

    //所需要的信息：返回二叉树的最大深度，节点个数
    public static class Message {
        public int depth;
        public int nodeNumber;

        public Message(int depth, int nodeNumber) {
            this.depth = depth;
            this.nodeNumber = nodeNumber;
        }
    }


    public Message process(Node node) {
        if (node == null) {
            return null;
        }

        Message leftMessage = process(node.left);
        Message rightMessage = process(node.right);

        int depth = Math.max(leftMessage.depth, rightMessage.depth) + 1;//最大深度要加上当前的节点这一层
        int nodeNumber = leftMessage.nodeNumber + rightMessage.nodeNumber + 1;//节点个数=左子树节点个数+右子树节点个数

        return new Message(depth, nodeNumber);
    }
}

如何判断一颗二叉树是否是平衡二叉树？ 

平衡二叉树

左子树与右子树的高度差不超过1

二叉树的递归套路

        问左树要的信息：左树是否是平衡二叉树；左树的高度

        问右树要的信息：右树是否是平衡二叉树；右树的高度

递归函数：返回是否为平衡二叉树，二叉树的深度

package binarytree;

public class IsBalancedBinaryTree {
    public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int data) {
            this.value = data;
        }
    }


    public boolean isBalancedBinaryTree(Node node) {
        return process(node).isBalance;
    }

    //所需要的信息：返回是否为平衡二叉树，二叉树的深度
    public static class Message {
        public boolean isBalance;
        public int depth;

        public Message(boolean isBalanced, int depth) {
            this.isBalance = isBalance;
            this.depth = depth;
        }
    }


    public Message process(Node node) {
        if (node == null) {
            return null;
        }

        Message leftMessage = process(node.left);//左边的信息
        Message rightMessage = process(node.right);//右边的信息

        int depth = Math.max(leftMessage.depth, rightMessage.depth) + 1;//最大深度要加上当前的节点这一层
        boolean isBalanced = leftMessage.isBalance && rightMessage.isBalance
                && (Math.abs(leftMessage.depth - rightMessage.depth) <= 1);
        //左右都为平衡二叉树并且左右子树深度差不超过1

        return new Message(isBalanced, depth);
    }
}

二叉树的递归套路

在文章中判断二叉树是否为完全二叉树/满二叉树/平衡二叉树等等的题型，都可以抽象出一个二叉树的递归套路

递归套路

树型DP问题（树上动态规划）可以用二叉树的递归套路来解

这里用文档注释表示具体需要写的代码

package binarytree;

public class Template {

    //Node类，节点
    public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int data) {
            this.value = data;
        }
    }

    //最终调用的函数，返回最后的结果
    public boolean judgment(Node node) {
        return true;//一般调用process函数获得Message对象，再获取Message对象里的信息
    }

    //Message类，信息
    //所需要的信息
    public static class Message {
        /*
        定义属性
         */

        //定义构造器
        public Message() {

        }
    }

    //具体的遍历过程
    public Message process(Node node){
        if (node == null) {
            return null;
        }
        
        Message leftMessage = process(node.left);//左边的信息
        Message rightMessage = process(node.right);//右边的信息
        
        /*
        具体判断具体分析，根据左右子树的属性获取总的这颗树的属性
         */
        
        //创建Message对象，把获取的属性赋值给新的属性，并返回
        return new Message();
    }
}

二叉树的递归套路解判断是否为搜索二叉树

        问左树要的信息：左树是否为搜索二叉树；左树的最大值（左树max < 当前节点的值）

        问右树要的信息：右树是否为搜索二叉树；右树的最小值（右树min > 当前节点的值）

递归函数：返回是否为搜索二叉树，二叉树的最大值，最小值

package binarytree;

public class IsSearchBinaryTree {

    public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int data) {
            this.value = data;
        }
    }


    public boolean isSearchBinaryTree(Node node) {
        return process(node).isSearch;
    }

    //所需要的信息：返回是否为搜索二叉树，二叉树的最大值，最小值
    public static class Message {
        public boolean isSearch;
        public int max;
        public int min;

        public Message(boolean isSearch, int max, int min) {
            this.isSearch = isSearch;
            this.max = max;
            this.min = min;
        }
    }


    public Message process(Node node){
        if (node == null) {
            return null;
        }

        Message leftMessage = process(node.left);//左边的信息
        Message rightMessage = process(node.right);//右边的信息

        int max = Math.max(leftMessage.max, rightMessage.max);
        max = Math.max(max,node.value);//当前节点和左右节点的值比较得出最大值
        int min = Math.min(leftMessage.min, rightMessage.min);
        min = Math.min(min,node.value);

        boolean isSearch = leftMessage.isSearch && rightMessage.isSearch
                && leftMessage.max < node.value && rightMessage.min > node.value;
        //左右子树都为搜索二叉树，左子树max < 当前节点的值 < 右子树min；暂不考虑等于的情况

        return new Message(isSearch,max,min);
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1125198.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【STL】priority_queue(优先级队列)详解及仿函数使用（附完整源码）

【STL】priority_queue(优先级队列)详解及仿函数使用（附完整源码）

目录 1. priority_queue介绍和使用1.1 priority_queue介绍1.2 priority_queue使用 2. 仿函数介绍3. priority_queue模拟实现 1. priority_queue介绍和使用 1.1 priority_queue介绍 优先级队列也是在<queue>里&#xff1a; 因此和queue一样&#xff0c;priority_queue也…
阅读更多...
java头歌-java中的异常

java头歌-java中的异常

文章目录 第一关第二关第三关第四关 第一关 第二关 题目要求&#xff1a; public static void main(String[] args) {Scanner sc new Scanner(System.in);try {int num1 sc.nextInt();int num2 sc.nextInt();/********* Begin *********/System.out.println(num1/num2);}…
阅读更多...
基于stm32控制的4G模块在设备模式下通讯

基于stm32控制的4G模块在设备模式下通讯

这里的32控制其实和51的控制思路都是一样的&#xff0c;都是先利用一个网络助手将家里的无线网生成局域网&#xff0c;接着通过花生壳软件将局域网变成公共网&#xff0c;最后是利用串口助手&#xff0c;在4G模块的AT指令模式写入命令ATSOCKTCPC,公共网IP地址,公共网端口号&…
阅读更多...
对话销售易CEO史彦泽：中国SaaS企业，利润和现金流从何而来？

对话销售易CEO史彦泽：中国SaaS企业，利润和现金流从何而来？

导读&#xff1a;SaaS企业如何快速转身&#xff0c;活下来 “华为应改变思路和经营方针&#xff0c;从追求规模转向追求利润和现金流&#xff0c;保证渡过未来三年的危机。把活下来作为最主要纲领&#xff0c;边缘业务全线收缩和关闭&#xff0c;把寒气传递给每个人。” 2022年…
阅读更多...
Pinia入门

Pinia入门

1. 什么是Pinia Pinia 是 Vue 的专属的最新状态管理库 &#xff0c;是 Vuex 状态管理工具的替代品 2. 手动添加Pinia到Vue项目 后面在实际开发Vue医疗项目的时候&#xff0c;Pinia可以在项目创建时自动添加&#xff0c;现在我们初次学习&#xff0c;从零开始&#xff1a; …
阅读更多...
Object.getPrototypeOf()

Object.getPrototypeOf()

1、作用 获取指定对象的原型&#xff08;内部​​[[Prototype]]​​属性的值&#xff09;&#xff0c;如果没有继承属性&#xff0c;则返回 null function Animal() {}var ani new Animal();console.log(ani);console.log(Object.getPrototypeOf(ani));2、注意 在 ES5 中&a…
阅读更多...
Http长连接同一个socket多个请求和响应如何保证一一对应?

Http长连接同一个socket多个请求和响应如何保证一一对应?

HTTP/2引入二进制数据帧和流的概念&#xff0c;其中帧对数据进行顺序标识&#xff0c;如下图所示&#xff0c;这样浏览器收到数据之后&#xff0c;就可以按照序列对数据进行合并&#xff0c;而不会出现合并后数据错乱的情况。同样是因为有了序列&#xff0c;服务器就可以并行的…
阅读更多...
视频去噪网络BSVD的实现

视频去噪网络BSVD的实现

前些天写了视频去噪网络BSVD论文的理解&#xff0c;详情请点击这里&#xff0c;这两个星期动手实践了一下&#xff0c;本篇就来记录一下这个模型的实现。 这个网络的独特之处在于&#xff0c;它的训练和推理在实现上有所差别。在训练阶段&#xff0c;其使用了TSM&#xff08;T…
阅读更多...
中国象棋棋盘识别

中国象棋棋盘识别

当象棋爱好者在挑战中国象棋残局或者在阅读象棋杀法书籍的时候遇到问题&#xff0c;往往需要通过象棋软件来辅助提示&#xff0c;此时要将该棋局在象棋软件中摆好&#xff0c;软件才能进行分析&#xff0c;为实现自动识别棋局图片&#xff0c;并导出为标准化FEN象棋文件格式&am…
阅读更多...
10.23

10.23

阅读更多...
Lec08 Page faults笔记总结

Lec08 Page faults笔记总结

当一个用户应用程序触发了page fault&#xff0c;page fault会使用与Robert教授上节课介绍的相同的trap机制&#xff0c;将程序运行切换到内核&#xff0c;同时也会将出错的地址存放在STVAL寄存器中。 在SCAUSE&#xff08;注&#xff0c;Supervisor cause寄存器&#xff0c;保…
阅读更多...
MyBatis-Plus实现逻辑删除[MyBatis-Plus系列] - 492篇

MyBatis-Plus实现逻辑删除[MyBatis-Plus系列] - 492篇

历史文章&#xff08;文章累计490&#xff09; 《国内最全的Spring Boot系列之一》 《国内最全的Spring Boot系列之二》 《国内最全的Spring Boot系列之三》 《国内最全的Spring Boot系列之四》 《国内最全的Spring Boot系列之五》 《国内最全的Spring Boot系列之六》 M…
阅读更多...
[Spring] SpringBoot2 简介（二）—— 高级配置

[Spring] SpringBoot2 简介（二）—— 高级配置

目录 一、Conditional 注解 1、SpringBoot 如何获取 Bean 对象 2、SpringBoot 创建 Condition 类 3、切换内置 web 服务器 二、EnableXXX 注解 1、SpringBoot 不能直接获取其他 jar 包/工程中的 Bean 2、原因分析 3、封装 Import 4、Import 注解 5、SpringBoot 自动配…
阅读更多...
前端领域的插件式设计

前端领域的插件式设计

插件&#xff0c;是一个常见的概念。 例如&#xff0c;当我们需要把我们前端代码中的 css 样式提取打包&#xff0c;我们可以用 webpack 的 mini-css-extract-plugin&#xff0c;或者你如果用 rollup 的话&#xff0c;可以选择 rollup-plugin-postcss。 再比如我们可以给 bab…
阅读更多...
Python 数组和列表：创建、访问、添加和删除数组元素

Python 数组和列表：创建、访问、添加和删除数组元素

Python 没有内置支持数组&#xff0c;但可以使用 Python 列表来代替。 数组 本页将向您展示如何使用列表作为数组&#xff0c;但要在 Python 中使用数组&#xff0c;您需要导入一个库&#xff0c;比如 NumPy 库。数组用于在一个变量中存储多个值&#xff1a; 示例&#xff0…
阅读更多...
VSCode 开发 Vue 语法提示

VSCode 开发 Vue 语法提示

一. 打开应用商店&#xff0c;搜索 vetur &#xff0c;选择第一个&#xff0c;点击安装。 二. 安装完成后&#xff0c;还可以下载 Vue Language Features 解决代码警告的问题。 最后重启 VSCode 就可以使用啦。另外输入 按回车键还可以自动生成 vue 代码格式哦。 原创作者&…
阅读更多...
GPT-3 内幕机制可视化解析

GPT-3 内幕机制可视化解析

GPT-3 内幕机制可视化解析 GPT-3是一个基于Transformer的语言模型，通过不同的层次提取语言不同层面的特性，构建整个语言的语义信息，它学习的过程跟人类正常学习的过程是类似的，开始的时候是一个无监督预训练，如图5-5所示，GPT-3模型可以将网络上的所有文档下载下来，包含 …
阅读更多...
AD9371 官方例程HDL详解之JESD204B TX侧时钟生成 （三）

AD9371 官方例程HDL详解之JESD204B TX侧时钟生成 （三）

AD9371 系列快速入口 AD9371ZCU102 移植到 ZCU106 &#xff1a; AD9371 官方例程构建及单音信号收发 ad9371_tx_jesd -->util_ad9371_xcvr接口映射&#xff1a; AD9371 官方例程之 tx_jesd 与 xcvr接口映射 AD9371 官方例程 时钟间的关系与生成 &#xff1a; AD9371 官方…
阅读更多...
Sui提供dApp Kit 助力快速构建React Apps和dApps

Sui提供dApp Kit 助力快速构建React Apps和dApps

近日&#xff0c;Mysten Labs推出了dApp Kit&#xff0c;这是一个全新的解决方案&#xff0c;可用于在Sui上开发React应用程序和去中心化应用程序&#xff08;dApps&#xff09;。mysten/dapp-kit是专门为React定制的全新SDK&#xff0c;旨在简化诸如连接钱包、签署交易和从RPC…
阅读更多...
Python生成词云

Python生成词云

成品&#xff1a; 代码&#xff1a; import os# 下面的两个包大家注意别导错了 from imageio.v2 import imread from wordcloud import wordcloud# mytext文本是字符串类型的 mytext str() # os.getcwd()是获得当前目录的路径&#xff0c;好像没啥用 读取 with open(os.getcw…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023