通过热敏电阻计算温度（二）—ODrive实现分析

ODrive计算热敏电阻的温度采用的时B值的方式计算的。首先根据公式计算出一系列的温度和测量点电压比例的点，然后通过多项式拟合曲线，得到三阶多项式的系数。后面便可以通过此三阶多项式来求解温度数据

测量原理图

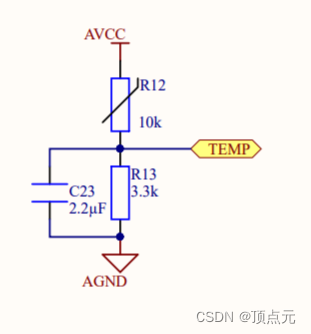
ODrive板卡上使用的热敏电阻的型号为NCP15XH103F03RC，10KΩ，25-80℃的B值为3428

计算分析

计算拟合的多项式系数

在tools->odrive->utils.py文件中有如下计算多项式系数的函数：

def calculate_thermistor_coeffs(degree, Rload, R_25, Beta, Tmin, Tmax, thermistor_bottom = False, plot = False):
    import numpy as np
    T_25 = 25 + 273.15 #Kelvin
    temps = np.linspace(Tmin, Tmax, 1000)
    tempsK = temps + 273.15

    # https://en.wikipedia.org/wiki/Thermistor#B_or_%CE%B2_parameter_equation
    r_inf = R_25 * np.exp(-Beta/T_25)
    R_temps = r_inf * np.exp(Beta/tempsK)
    if thermistor_bottom:
        V = R_temps / (Rload + R_temps)
    else:
        V = Rload / (Rload + R_temps)

    fit = np.polyfit(V, temps, degree)
    p1 = np.poly1d(fit)
    fit_temps = p1(V)

    if plot:
        import matplotlib.pyplot as plt
        print(fit)
        plt.plot(V, temps, label='actual')
        plt.plot(V, fit_temps, label='fit')
        plt.xlabel('normalized voltage')
        plt.ylabel('Temp [C]')
        plt.legend(loc=0)
        plt.show()

    return p1

np.linspace(start, stop, num)函数用于以均匀间隔创建对应num数的数值序列。
np.polyfit(x,y,deg)函数用于对一组数据采用最小二乘法进行多项式拟合，返回值为多项式系数,deg表示多项式的阶数
np.poly1d(c)c表示多项式系数，用于根据多项式系数生成多项式（这里介绍的是仅有一个参数的情况）

根据多项式方程计算温度的函数

在MotorControl->utils.hpp文件中根据多项式系数计算温度的函数

// Evaluate polynomials in an efficient way
// coeffs[0] is highest order, as per numpy.polyfit
// p(x) = coeffs[0] * x^deg + ... + coeffs[deg], for some degree "deg"
inline float horner_poly_eval(float x, const float *coeffs, size_t count) {
    float result = 0.0f;
    for (size_t idx = 0; idx < count; ++idx)
        result = (result * x) + coeffs[idx];
    return result;
}

数组coeffs[4]存储了多项式的系数，coeffs[0]表示最高阶的系数。

温度计算调用函数

void ThermistorCurrentLimiter::update() {
    const float normalized_voltage = get_adc_relative_voltage_ch(adc_channel_);
    float raw_temperature_ = horner_poly_eval(normalized_voltage, coefficients_, num_coeffs_);

    constexpr float tau = 0.1f; // [sec]
    float k = current_meas_period / tau;
    float val = raw_temperature_;
    for (float& lpf_val : lpf_vals_) {
        lpf_val += k * (val - lpf_val);
        val = lpf_val;
    }
    if (is_nan(val)) {
        lpf_vals_.fill(0.0f);
    }
    temperature_ = lpf_vals_.back();
}

normalized_voltage为根据adc的值转化过来的0-1之间的值。代入horner_poly_eval()函数可以的得到原始的温度数据。后面的部分是对温度数据的低通滤波处理。