目录
- 计算条件概率
- 计算概率(放回与不放回)
- 生成随机数算法
- Linear Congruential Method
- 判断是否是full period
- Uniformity (test of frequency)
- 1.Chi-Square test
- method
- reminder
- example
- 2.Kolmogorov-Sminov test
- method
- example
- Independence (test of autocorrelation)
- Runs test
- Acceptance-rejection method
- method
- 方法1:建议函数使用指数分布
- 方法2:双指数分布生成正态分布
- 方法3:
- 使用Acceptance-Rejection method对连续型随机变量有效,证明处处都有 P ( X ≤ x ) = F X ( x ) P(X≤x)=F_X(x) P(X≤x)=FX(x)
- Empirical distribution 经验分布
- The Empirical Distribution Procedure
- Ungrouped data
- condition
- method
- construction method
- 生成U去寻找x
- grouped data
- condition
- construction method
- example
- How about discrete empirical distribution?
- 经验分布的优点与缺点
- example
- Maximum Likelihood Estimator 最大似然估计
- 判断数据是否相互独立
计算条件概率
【作业题】
Suppose that Die-Hardly-Ever battery has an exponential time-to-failure
distribution with a mean of 48 months. At 60 months, the battery is still operating.
- What is the probability that this battery is going to die in the next 12 months?
- What is the probability that the battery dies in an odd year of its life?
- If the battery is operating at 60 months, compute the expected additional months of life.
【重点】条件概率+指数分布无记忆性
即
P
(
x
>
s
+
t
∣
x
>
t
)
=
P
(
x
>
s
)
P(x>s+t|x>t)=P(x>s)
P(x>s+t∣x>t)=P(x>s)
计算概率(放回与不放回)
Suppose that a man has k keys, one of which will open a door. Compute
the expected number of keys required to open the door for the following two cases:
a. The keys are tried one at a time without replacement.(不放回)
b. The keys are tried one at time with replacement.(放回)

生成随机数算法
Linear Congruential Method

判断是否是full period
 【作业题】可能考察是否full period
【作业题】可能考察是否full period
R
i
=
X
i
m
<
1
R_i=\frac{X_i}{m}<1
Ri=mXi<1

Uniformity (test of frequency)
检验样本是否服从均匀分布
对前提进行假设
F
r
e
q
u
e
n
c
y
Frequency
Frequency
H
0
:
R
i
′
s
U
(
0
,
1
)
H_0:R_i's~U(0,1)
H0:Ri′s U(0,1)
H
1
:
R
i
′
s
n
o
t
U
(
0
,
1
)
H_1:R_i's not U(0,1)
H1:Ri′snotU(0,1)
在测试前要说明清楚,显著性水平
α
=
P
(
t
y
p
e
o
n
e
e
r
r
o
r
)
=
p
(
r
e
j
e
c
t
H
0
∣
H
0
i
s
t
r
u
e
)
\alpha=P(type\ one\ error)=p(reject\ H_0|H_0 is\ true)
α=P(type one error)=p(reject H0∣H0is true)
1.Chi-Square test
- 卡方检验的期望值 E i E_i Ei要求 E i ≥ 5 E_i≥5 Ei≥5【这个是为了确保近似分布是合理的】
method
检验是否服从 U ( 0 , 1 ) U(0, 1) U(0,1)如下,
- 将[0,1]分成k个等长子区间(对应Reminder的Equal probability)
- 计算 O j O_j Oj,其为样本数据 R i R_i Ri落在子区间 ( j − 1 k , j k ] (\frac{j-1}{k},\frac{j}{k}] (kj−1,kj]的频次
- E j = E ( O j ) = n k E_j=E(O_j)=\frac{n}{k} Ej=E(Oj)=kn观测值在j区间的期望
- 计算卡方 X 0 2 = ∑ j = 1 k ( O j − E j ) 2 E j {X_0}^2=\sum_{j=1}^{k}{\frac{(O_j-E_j)^2}{E_j}} X02=∑j=1kEj(Oj−Ej)2
- Reject Ho if X 0 2 > X k − 1 , α 2 {X_0}^2>X_{k-1,\alpha}^2 X02>Xk−1,α2
reminder

example
Using appropriate test, check whether the numbers are uniformly distributed: 0.594, 0.928, 0.515, 0.055, 0.507, 0.351, 0.262, 0.797, 0.788, 0.442, 0.097, 0.798, 0.227, 0.127, 0.474, 0.825, 0.007, 0.182, 0.929, 0.852.
即判断数据是否服从均匀分布。
int main(){
#ifdef local
freopen("data.txt", "r", stdin);
// freopen("data.txt", "w", stdout);
#endif
int n = 20;
rep(i, 1, n){
cin >> a[i];
}
sort(a+1, a+n+1);
rep(i, 1, n){
cout << " " << a[i];
}
}
排序可得(共20个数据)
0.007 0.055 0.097 0.127 0.182 0.227
0.262 0.351 0.442 0.474
0.507 0.515 0.594
0.788 0.797 0.798 0.825 0.852 0.928 0.929
要求期望Ei是大于5的,所以应该分为4个区间。如下
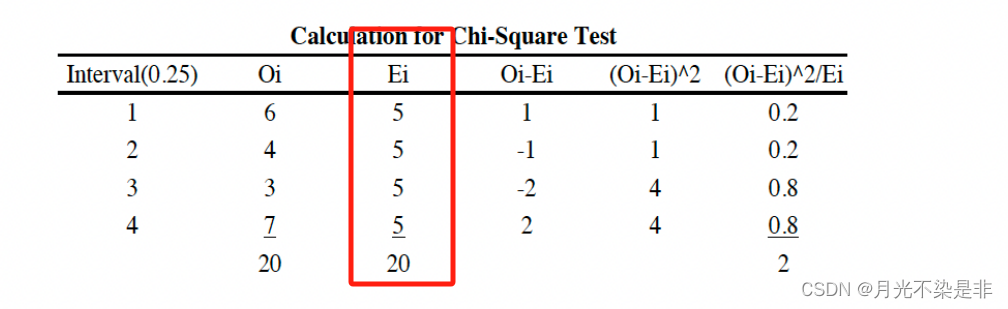
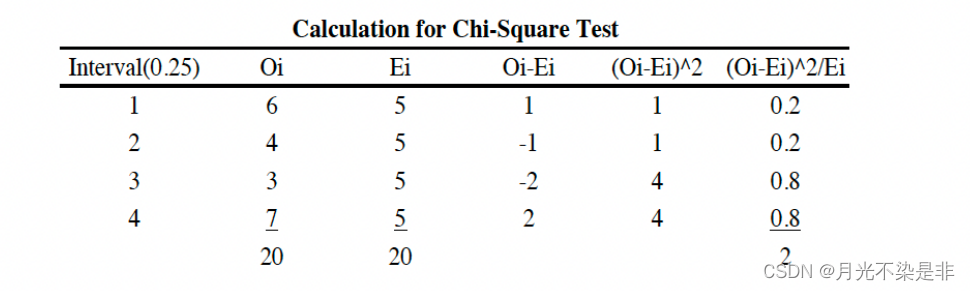

2.Kolmogorov-Sminov test
KS检测,主要用于检测数据是否符合某种分布
method
- Rank R ( 1 ) ≤ R ( 2 ) ≤ . . . ≤ R ( N ) R_{(1)}≤R_{(2)}≤...≤R_{(N)} R(1)≤R(2)≤...≤R(N)
- compute
D
+
=
max
1
≤
i
≤
N
{
i
N
−
R
(
i
)
}
D^+=\max_{1≤i≤N}\{\frac{i}{N}-R_{(i)}\}
D+=1≤i≤Nmax{Ni−R(i)}
D − = max 1 ≤ i ≤ N { R ( i ) − i − 1 N } D^-=\max_{1≤i≤N}\{R_{(i)}-\frac{i-1}{N}\} D−=1≤i≤Nmax{R(i)−Ni−1} - compute D = m a x ( D + , D − ) D=max(D^+, D^-) D=max(D+,D−)
- 拒绝 H 0 H_0 H0 if D > D α ( N ) D>D_{\alpha}(N) D>Dα(N)
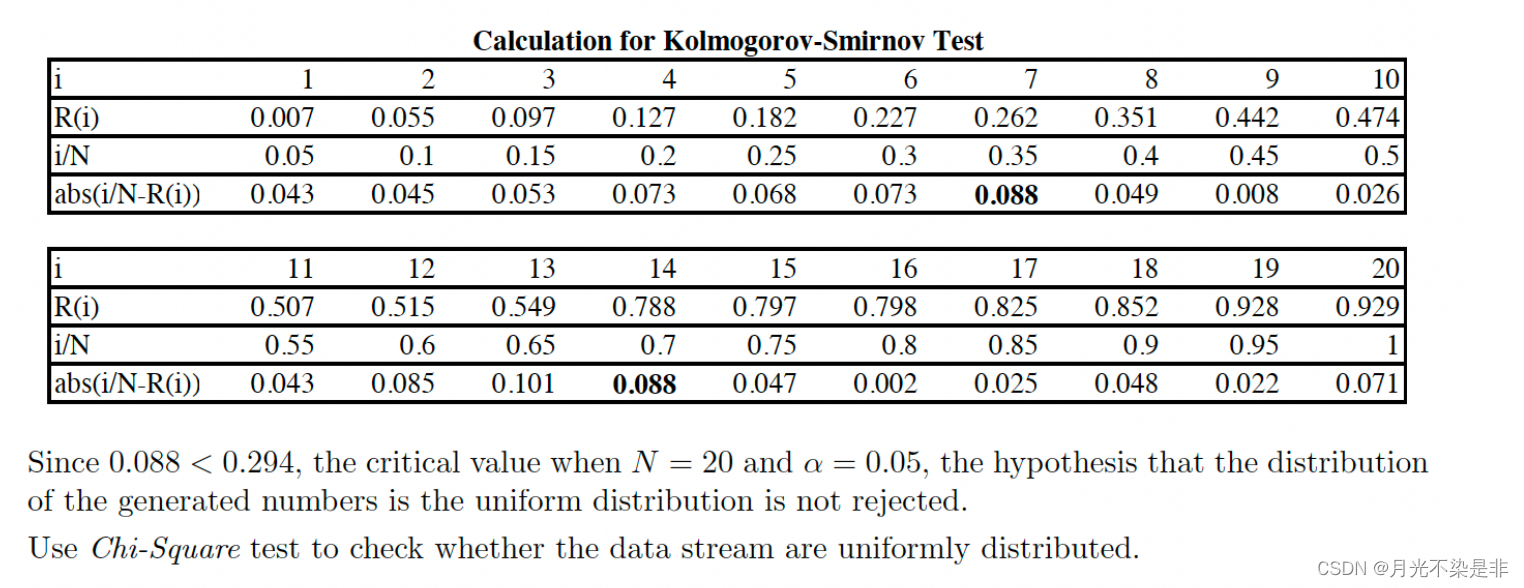
example
Using appropriate test, check whether the numbers are uniformly distributed: 0.594, 0.928, 0.515, 0.055, 0.507, 0.351, 0.262, 0.797, 0.788, 0.442, 0.097, 0.798, 0.227, 0.127, 0.474, 0.825, 0.007, 0.182, 0.929, 0.852.
即判断数据是否服从均匀分布。
Independence (test of autocorrelation)
Runs test
Acceptance-rejection method
This method uses an auxiliary function t(x) that is everywhere ≥ the density f(x) of the RV X we want to simulate
接受-拒绝采样,这个方法使用一个辅助函数
t
(
x
)
t(x)
t(x),
t
(
x
)
t(x)
t(x)函数满足处处
t
(
x
)
≥
f
(
x
)
t(x)≥f(x)
t(x)≥f(x),
f
(
x
)
f(x)
f(x)是随机变量X的概率密度函数,X就是我们想要进行模拟的随机变量。
显然,处处 t ( x ) ≥ 0 t(x)≥0 t(x)≥0
引入 t ( x ) t(x) t(x)去求解 c c c
不妨,令 r ( x ) = t ( x ) c r(x)=\frac{t(x)}{c} r(x)=ct(x),其一定为概率密度
我们必须选择 t t t,以此能更轻松的从 r ( x ) r(x) r(x)概率密度函数中采样。
method
- 从概率密度r(x)中产生Y
- 产生均匀分布U(0, 1)变量U,其独立于Y
- 这意味着我们必须使用其他的随机变量
- 当 U ≤ f ( Y ) t ( Y ) U≤\frac{f(Y)}{t(Y)} U≤t(Y)f(Y)时,则令 X = Y X=Y X=Y,否则就回到第一步重新产生Y。
例题 Problem 7: Give an algorithm for generating a standard normal random variable X ∼ N(0,1).
(Hint: if we can generate from the absolute value |X|, then by symmetry we can obtain X by independently generating a rv U (for sign) that is ±1 with probability 1/2 and setting X = U|X|.)
方法1:建议函数使用指数分布
(1)前提准备
首先,根据已知分布的概率密度函数f(x),产生服从此分布的样本X
f ( x ) = 1 2 π e − x 2 2 ( − ∞ < x < + ∞ ) f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} (-\infty<x<+\infty) f(x)=2π1e−2x2(−∞<x<+∞)
但根据题目提示,我们仅能产生|X|,不过同理,不妨设随机变量Z,
Z
=
∣
X
∣
Z=|X|
Z=∣X∣,由X的概率密度函数我们可以知道Z的概率密度函数
f
Z
(
z
)
=
2
2
Π
e
−
z
2
2
(
z
≥
0
)
f_Z(z)=\frac{2}{\sqrt{2Π}}e^{-\frac{z^2}{2}} (z≥0)
fZ(z)=2Π2e−2z2(z≥0)
此时再找一个建议函数(辅助函数),即随机变量Y,其服从指数分布,故我们可得其概率密度函数
f
Y
(
y
)
=
λ
e
−
λ
y
(
y
>
0
)
f_Y(y)=\lambda e^{-\lambda y} (y>0)
fY(y)=λe−λy(y>0)
(2)我们首先得确定建议函数的参数
λ
\lambda
λ与Acceptance-rejection method的参数c(在Acceptance-rejection method算法中我们希望c能接近1)
c ∗ g ( x ) ≥ f ( x ) c*g(x)≥f(x) c∗g(x)≥f(x),g(x)为建议函数
c
f
Y
(
u
)
f
Z
(
u
)
=
c
λ
e
−
λ
u
2
2
π
e
−
u
2
2
=
c
λ
2
π
2
e
1
2
(
u
−
λ
)
2
−
λ
2
2
\frac{cf_Y(u)}{f_Z(u)}=\frac{c\lambda e^{-\lambda u}} {\frac{2}{\sqrt{2\pi}}e^{-\frac{u^2}{2}}}= \frac{c\lambda\sqrt{2\pi}}{2}e^{\frac{1}{2}(u-\lambda)^2-\frac{\lambda^2}{2}}
fZ(u)cfY(u)=2π2e−2u2cλe−λu=2cλ2πe21(u−λ)2−2λ2
易得
c
λ
2
π
2
e
1
2
(
u
−
λ
)
2
−
λ
2
2
≥
c
λ
2
π
2
e
−
λ
2
2
\frac{c\lambda\sqrt{2\pi}}{2}e^{\frac{1}{2}(u-\lambda)^2-\frac{\lambda^2}{2}}≥c\frac{\lambda\sqrt{2\pi}}{2}e^{-\frac{\lambda^2}{2}}
2cλ2πe21(u−λ)2−2λ2≥c2λ2πe−2λ2
不妨令
λ
=
1
\lambda=1
λ=1,
c
=
2
2
π
e
1
2
c=\frac{2}{\sqrt{2\pi}}e^{\frac{1}{2}}
c=2π2e21
(这么令代入便于计算)
即可以满足
c
f
Y
(
u
)
f
Z
(
u
)
≥
1
\frac{cf_Y(u)}{f_Z(u)}≥1
fZ(u)cfY(u)≥1
此时确定可以将
f
Y
(
u
)
f_Y(u)
fY(u)作为我们的建议函数(辅助函数)
t
(
y
)
=
c
f
Y
(
y
)
t(y)=cf_Y(y)
t(y)=cfY(y)
(课件中使用t(x)代表建议函数,故此用t表示)
(3)由(2)已将建议函数 t ( y ) = c f Y ( y ) t(y)=cf_Y(y) t(y)=cfY(y)找好,接下来我们从中进行采样
【第一个是为了得到样本Y】
- 生成随机变量U1,其服从U(0,1)的均匀分布,从中生成u1,从而获得采样点y
y = F − 1 ( u 1 ) = − l n ( 1 − u 1 ) y=F^{-1}(u1)=-ln(1-u_1) y=F−1(u1)=−ln(1−u1)(这个可由指数分布的分布函数去进行求逆变换得到)
【第二个是为了得到样本U】
- 再生成一个随机变量U2,其也服从U(0, 1)的均匀分布,从中得到u2,且随机变量U1和U2相互独立
if u 1 ≤ f Z ( y ) c f Y ( y ) u1≤\frac{f_Z(y)}{cf_Y(y)} u1≤cfY(y)fZ(y)
则该采样点可以取到,(接受)Z=y
否则就拒绝回到(3)的开始重新进行采样。
(4)综上,我们产生了Z,其满足 Z = ∣ X ∣ Z=|X| Z=∣X∣,但我们实际求解的是X
- 因此,再生成一个随机变量U3,其服从U(0, 1)的均匀分布,从中得到u3,且随机变量U3是独立于U1、U2
m = { + 1 u3 ≤ 0.5 − 1 u3 > 0.5 m=\begin{cases} +1& \text{u3 ≤ 0.5}\\ -1& \text{u3 > 0.5} \end{cases} m={+1−1u3 ≤ 0.5u3 > 0.5
故 X = m ∗ Z X=m*Z X=m∗Z即为采样所得服从N(0,1)标准正态分布
方法2:双指数分布生成正态分布
- 产生两个相互独立服从参数为1的指数分布的随机变量Y1、Y2
Y 1 = − l n ( U 1 ) Y1=-ln(U_1) Y1=−ln(U1)
and Y 2 = − l n ( U 2 ) Y2=-ln(U_2) Y2=−ln(U2) - 当 Y 2 ≥ ( Y 1 − 1 ) 2 2 Y_2≥\frac{(Y_1-1)^2}{2} Y2≥2(Y1−1)2时,令 ∣ Z ∣ = Y 1 |Z|=Y_1 ∣Z∣=Y1否则就回到第一步重新进行采样
- 生成随机变量U,其服从均匀分布U(0, 1)
Z = { ∣ Z ∣ U ≤ 0.5 − ∣ Z ∣ U > 0.5 Z=\begin{cases} |Z|& \text{U ≤ 0.5}\\ -|Z|& \text{U > 0.5} \end{cases} Z={∣Z∣−∣Z∣U ≤ 0.5U > 0.5
方法3:
- 生成随机变量Y,其服从参数为1的指数分布;生成随机变量U1,并令 Y = − l n ( U 1 ) Y=-ln(U1) Y=−ln(U1)
- 生成随机变量U2
- 若 U 2 ≤ e − ( Y − 1 ) 2 2 U2≤e^{-\frac{(Y-1)^2}{2}} U2≤e−2(Y−1)2则令|Z|=Y,否则则回到第一步
- 生成U3,若U3≤0.5则Z=|Z|;若U3>0.5,则Z=-|Z|
注意第3步,
U
2
≤
e
−
(
Y
−
1
)
2
2
U2≤e^{-\frac{(Y-1)^2}{2}}
U2≤e−2(Y−1)2,可得
−
l
n
(
U
2
)
≥
(
Y
−
1
)
2
/
2
-ln(U2)≥(Y-1)^2/2
−ln(U2)≥(Y−1)2/2
就可以简化
−
l
n
(
U
2
)
-ln(U2)
−ln(U2)是服从参数为1的指数分布。
使用Acceptance-Rejection method对连续型随机变量有效,证明处处都有 P ( X ≤ x ) = F X ( x ) P(X≤x)=F_X(x) P(X≤x)=FX(x)
设,事件A为接受事件,由Acceptance-Rejection method可知,当A发生时,可将采样Y去代替X,即X=Y
左边
=
P
(
X
≤
x
)
=
P
(
Y
≤
x
∣
A
)
=
P
(
Y
≤
x
,
A
)
P
(
A
)
左边=P(X≤x)=P(Y≤x|A)=\frac{P(Y≤x,A)}{P(A)}
左边=P(X≤x)=P(Y≤x∣A)=P(A)P(Y≤x,A)
对Y进行采样,得到y,可以取Y作为X的概率如下,
P
(
A
∣
Y
=
y
)
=
P
(
U
≤
f
(
y
)
t
(
y
)
)
=
f
(
y
)
t
(
y
)
P(A|Y=y)=P(U≤\frac{f(y)}{t(y)})=\frac{f(y)}{t(y)}
P(A∣Y=y)=P(U≤t(y)f(y))=t(y)f(y)
t(y)为建议分布的概率密度函数
U服从U(0, 1)的均匀分布,故概率如上。
则
0
≤
f
(
y
)
t
(
y
)
≤
1
0≤\frac{f(y)}{t(y)}≤1
0≤t(y)f(y)≤1
即
f
(
y
)
≤
t
(
y
)
f(y)≤t(y)
f(y)≤t(y)
取r(y)为Y的概率密度函数
P
(
A
a
n
d
Y
≤
x
)
=
∫
−
∞
x
P
(
A
a
n
d
Y
≤
x
∣
Y
=
y
)
r
(
y
)
d
y
P(A\ and\ Y ≤ x)=\int_{-\infty}^xP(A\ and\ Y ≤x|Y=y)r(y)dy
P(A and Y≤x)=∫−∞xP(A and Y≤x∣Y=y)r(y)dy
由区间知Y≤x必然成立,故
P
(
A
a
n
d
Y
≤
x
)
=
∫
−
∞
x
P
(
A
a
n
d
Y
≤
x
∣
Y
=
y
)
r
(
y
)
d
y
=
∫
−
∞
x
P
(
A
∣
Y
=
y
)
r
(
y
)
d
y
=
∫
−
∞
x
f
(
y
)
t
(
y
)
∗
t
(
y
)
c
d
y
=
1
c
∫
−
∞
x
f
(
y
)
d
y
=
1
c
F
(
x
)
P(A\ and\ Y ≤ x)=\int_{-\infty}^xP(A\ and\ Y ≤x|Y=y)r(y)dy\\= \int_{-\infty}^xP(A|Y=y)r(y)dy\\ =\int_{-\infty}^x\frac{f(y)}{t(y)}*\frac{t(y)}{c}dy\\ =\frac{1}{c}\int_{-\infty}^xf(y)dy\\ =\frac{1}{c}F(x)
P(A and Y≤x)=∫−∞xP(A and Y≤x∣Y=y)r(y)dy=∫−∞xP(A∣Y=y)r(y)dy=∫−∞xt(y)f(y)∗ct(y)dy=c1∫−∞xf(y)dy=c1F(x)
又因为 P ( A ) = ∫ R P ( A ∣ Y = y ) r ( y ) d y = 1 c ∫ R f ( y ) d y = 1 c P(A)=\int_R P(A|Y=y)r(y)dy\\ =\frac{1}{c}\int_R f(y)dy=\frac{1}{c} P(A)=∫RP(A∣Y=y)r(y)dy=c1∫Rf(y)dy=c1即 P ( A ) = 1 c P(A)=\frac{1}{c} P(A)=c1
已知, = P ( X ≤ x ) = P ( Y ≤ x ∣ A ) = P ( Y ≤ x , A ) P ( A ) =P(X≤x)=P(Y≤x|A)=\frac{P(Y≤x,A)}{P(A)} =P(X≤x)=P(Y≤x∣A)=P(A)P(Y≤x,A)
将 P ( A a n d Y ≤ x ) = 1 c F ( x ) P(A\ and\ Y ≤ x)=\frac{1}{c}F(x) P(A and Y≤x)=c1F(x)带入
将 P ( A ) = 1 c P(A)=\frac{1}{c} P(A)=c1带入
解得, P ( X ≤ x ) = F ( x ) P(X≤x)=F(x) P(X≤x)=F(x),综上得证。
Empirical distribution 经验分布
连续型经验分布是分段线性不是阶梯式
The Empirical Distribution Procedure

重点:数据是否已经被分组
Ungrouped data
condition
当原始的数据已知且有具体的值的时候
method
这里我们可以使用插值法。
首先我们得到的是一组未经处理的数据,不妨设有n个
然后,根据数值由小到大对其进行排序,
- 最小的值到 [ 0 , 1 n − 1 ] [0, \frac{1}{n-1}] [0,n−11]
- 接下来的值放到 [ 1 n − 1 , 2 n − 1 ] [\frac{1}{n-1}, \frac{2}{n-1}] [n−11,n−12]
- 继续上述类似操作
- 最大值分配到1上
这样,每个值都会和一个区间相对应
construction method
定义一个连续的、分段线性的分布函数F
将Xi单调递增排序,Xi表示第i小(Xi就是排序过的数值),此时可以得到F函数如下
{
0
,
if
x
<
X
(
1
)
i
−
1
n
+
1
+
x
−
X
i
(
n
−
1
)
(
X
(
i
+
1
)
−
X
(
i
)
)
,
if
X
i
≤
x
<
X
(
i
+
1
)
,
∀
i
<
n
−
1
1
,
if
X
(
n
)
<
x
\begin{cases} 0& ,\text{if $x<X_{(1)}$}\\ \frac{i-1}{n+1}+\frac{x-X_i}{(n-1)(X_{(i+1)}-X_{(i)})}& ,\text{if $X_i≤x<X_{(i+1)}$, $\forall i<n-1$}\\ 1& ,\text{if $X_{(n)}<x$} \end{cases}
⎩
⎨
⎧0n+1i−1+(n−1)(X(i+1)−X(i))x−Xi1,if x<X(1),if Xi≤x<X(i+1), ∀i<n−1,if X(n)<x
生成U去寻找x

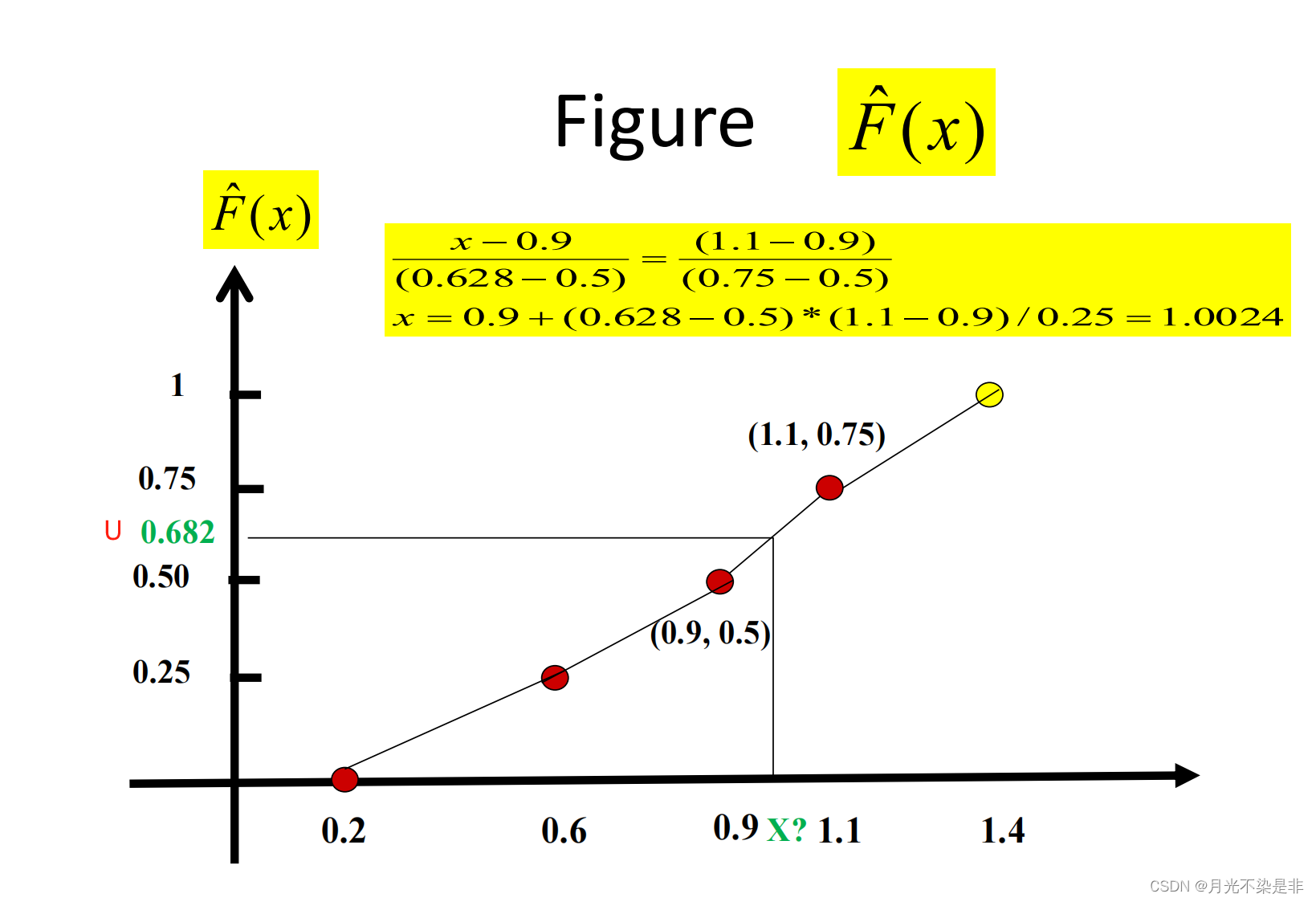
grouped data
condition
我们没有独立的数据样本点的时候,仅知道每组数据间隔中有多少数据,即
- n j n_j nj个点在区间 [ a j − 1 , a j ] , j = 0 , , , , , k [a_{j-1},a_j],j=0,,,,,k [aj−1,aj],j=0,,,,,k
- ∑ n j = n \sum n_j=n ∑nj=n
- 令 G ( a j ) = ( n 1 + . . . + n j ) / n , j ≥ 1 , G ( a 0 ) = 0 G(a_j)=(n_1+...+n_j)/n,j≥1,G(a_0)=0 G(aj)=(n1+...+nj)/n,j≥1,G(a0)=0
- 分配
a
j
a_j
aj到
[
G
(
a
j
)
,
G
(
a
j
+
1
)
]
[G(a_j), G(a_{j+1})]
[G(aj),G(aj+1)],剩下的数据也如上处理
最后将0值分配给任意x<a0即可
construction method
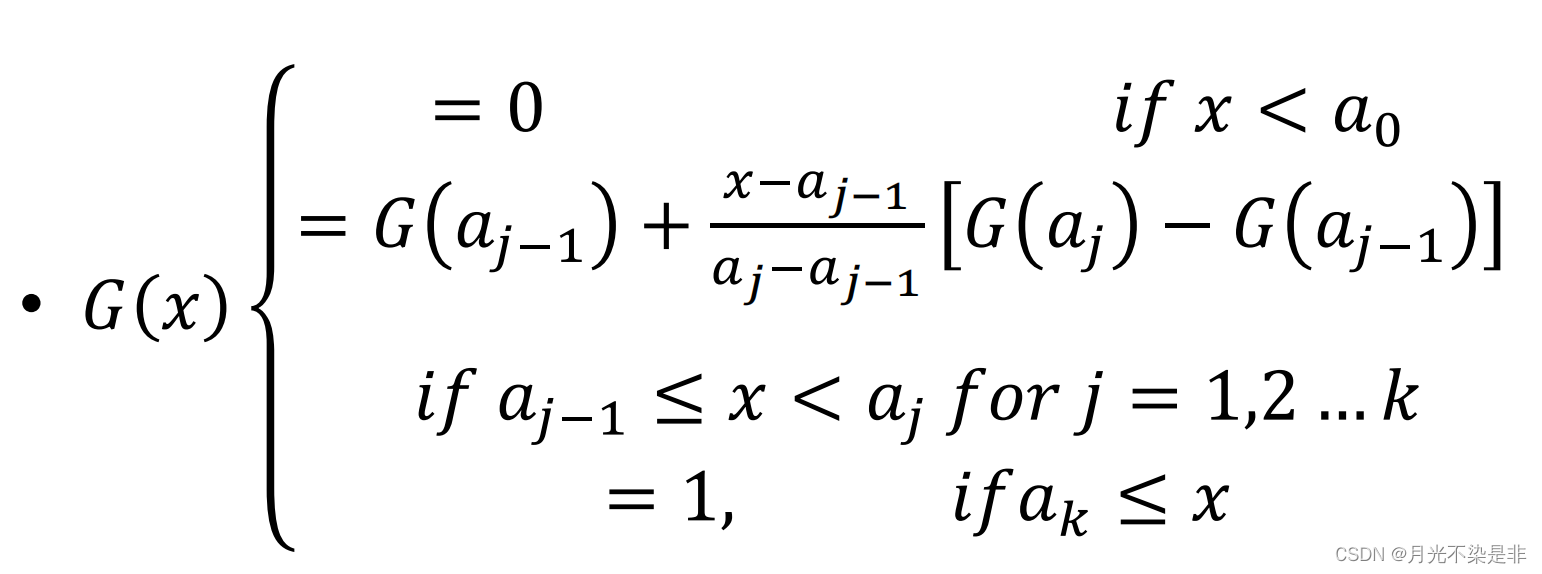
example

How about discrete empirical distribution?
- Data Are Not Grouped
对于数值x,定义p(x)为 值为x的数值个数占所有数值个数的比例 - Only Grouped Data Are Available
定义一个概率函数,使得一个区间内所有数值的概率之和为该区间数值个数占所有数值个数之比
经验分布的优点与缺点
优点
- 使用当前数据
- 易于操作
缺点
- 无法得到观察值范围外的数据
- 看起来不规则
example
Data have been collected on service times at a drive-in-bank window at the Shady Lane National Bank. The data are summarized into intervals as follows:
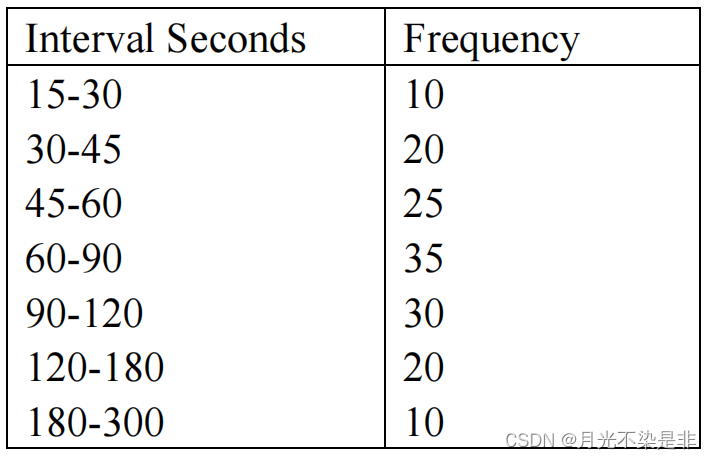
Set up a table like examples which has been discussed in class, for generating service
times by the table-lookup method. Generate five values of service time using random
numbers 0.9473, 0.0823, 0.3561, 0.2482, and 0.8831.
- 首先判断grouped or ungrouped - 显然是grouped 即没有独立的样本点,只有区间样本数
- 要算概率、累计概率、斜率、最后根据概率估算x
| Interval Seconds | Frequency | probability | cumulative pro | Slope |
|---|---|---|---|---|
| 15-30 | 10 | 1 15 \frac{1}{15} 151 | 1 15 \frac{1}{15} 151 | 225 |
| 30-45 | 20 | 2 15 \frac{2}{15} 152 | 1 5 \frac{1}{5} 51 | 225 2 \frac{225}{2} 2225 |
| 45-60 | 25 | 1 6 \frac{1}{6} 61 | 11 30 \frac{11}{30} 3011 | 90 |
| 60-90 | 35 | 7 30 \frac{7}{30} 307 | 3 5 \frac{3}{5} 53 | 900 7 \frac{900}{7} 7900 |
| 90-120 | 30 | 1 5 \frac{1}{5} 51 | 4 5 \frac{4}{5} 54 | 150 |
| 120-180 | 20 | 2 15 \frac{2}{15} 152 | 14 15 \frac{14}{15} 1514 | 450 |
| 180-300 | 10 | 1 15 \frac{1}{15} 151 | 1 | 1800 |
由图可知:
X
0
=
15
,
X
1
=
30
,
X
2
=
45
,
.
.
.
,
X
7
=
300
X_0=15,X_1=30,X_2=45,...,X_7=300
X0=15,X1=30,X2=45,...,X7=300
计算斜率:
a
i
=
X
i
−
X
i
−
1
C
u
m
u
l
a
t
i
v
e
P
(
X
i
)
−
C
u
m
u
l
a
t
i
v
e
P
(
X
i
−
1
)
a_i=\frac{X_i-X_{i-1}}{CumulativeP(X_i)-CumulativeP(X_{i-1})}
ai=CumulativeP(Xi)−CumulativeP(Xi−1)Xi−Xi−1
a
1
=
30
−
15
1
15
=
225
a1=\frac{30-15}{\frac{1}{15}}=225
a1=15130−15=225
a
2
=
45
−
30
2
15
=
225
2
a2=\frac{45-30}{\frac{2}{15}}=\frac{225}{2}
a2=15245−30=2225
其余斜率求解方法相同,接下来根据概率求解x值
如 F ( x ) = 0.9473 F(x)=0.9473 F(x)=0.9473
易知, F ( x ) > 14 15 F(x)>\frac{14}{15} F(x)>1514
x = 180 + ( 0.9473 − 0.9333 ) ∗ 1800 = 205.14 x=180+(0.9473-0.9333)*1800=205.14 x=180+(0.9473−0.9333)∗1800=205.14
其余同理。
Maximum Likelihood Estimator 最大似然估计
例题: Consider the shifted (two-parameter) exponential distribution, which has
density function
f
(
x
)
=
{
1
β
e
−
(
x
−
γ
)
/
β
if
x
≥
γ
0
otherwise
f(x)=\begin{cases} \frac{1}{\beta} e^{-(x-\gamma)/\beta}& \text{if $x≥\gamma$}\\ 0& \text{otherwise} \end{cases}
f(x)={β1e−(x−γ)/β0if x≥γotherwise
for
β
>
0
\beta > 0
β>0 and any real number
γ
\gamma
γ. Given a sample
X
1
,
X
2
,
X
3
,
.
.
.
,
X
n
X_1,X_2,X_3,...,X_n
X1,X2,X3,...,Xn of IID random values
from this distribution, find formulas for the joint MLEs
γ
^
\hat{\gamma}
γ^ and
β
^
\hat{\beta}
β^ .
求解如下:
可得最大似然函数
L
(
γ
,
β
)
=
1
β
n
e
x
p
[
−
∑
i
=
1
n
(
X
i
−
γ
)
/
β
]
L(\gamma, \beta)=\frac{1}{{\beta}^n}exp[-\sum_{i=1}^n(X_i-\gamma)/\beta]
L(γ,β)=βn1exp[−i=1∑n(Xi−γ)/β]
上式必然满足
X
i
≥
γ
X_i≥\gamma
Xi≥γ对于所有的
i
i
i
两侧同时取对数
l
(
γ
,
β
)
=
l
n
(
L
(
γ
,
β
)
)
=
−
n
l
n
(
β
)
−
[
∑
i
=
1
n
(
X
i
−
γ
)
/
β
]
=
−
n
l
n
(
β
)
−
1
β
∑
i
=
1
n
X
i
+
n
γ
β
l(\gamma,\beta)=ln(L(\gamma,\beta))=-nln(\beta)-[\sum_{i=1}^n(X_i-\gamma)/\beta]\\ =-nln(\beta)-\frac{1}{\beta}\sum_{i=1}^{n}X_i+n\frac{\gamma}{\beta}
l(γ,β)=ln(L(γ,β))=−nln(β)−[i=1∑n(Xi−γ)/β]=−nln(β)−β1i=1∑nXi+nβγ
我们已知,
β
>
0
\beta>0
β>0,想要越大的
n
γ
β
n\frac{\gamma}{\beta}
nβγ,
γ
\gamma
γ就得越大
例如
γ
=
X
(
1
)
\gamma=X_{(1)}
γ=X(1),我们就等于要最大化
g
(
β
)
g(\beta)
g(β)
g
(
β
)
=
−
n
l
n
(
β
)
−
1
β
∑
i
=
1
n
X
i
+
n
x
(
1
)
β
g(\beta)=-nln(\beta)-\frac{1}{\beta}\sum_{i=1}^{n}X_i+n\frac{x_{(1)}}{\beta}
g(β)=−nln(β)−β1i=1∑nXi+nβx(1)
综上可解得,
β
^
=
X
‾
(
n
)
−
X
(
1
)
\hat{\beta}=\overline{X}(n)-X_{(1)}
β^=X(n)−X(1)
也可写作
β
^
=
X
‾
(
n
)
−
γ
^
\hat{\beta}=\overline{X}(n)-\hat{\gamma}
β^=X(n)−γ^但
γ
是有
^
\gamma是有\ \hat{}
γ是有 ^
要注意,尽管我们需要尽可能大的
γ
\gamma
γ,但是也要满足
X
≥
γ
X≥\gamma
X≥γ,也就是最大的
γ
\gamma
γ也只能取得最小的
X
i
X_i
Xi
X
(
1
)
=
m
i
n
{
X
1
,
X
2
,
.
.
.
,
X
n
}
X_{(1)}=min\{X_1,X_2,...,X_n\}
X(1)=min{X1,X2,...,Xn}