1.算法描述

WOA算法设计的既精妙又富有特色，它源于对自然界中座头鲸群体狩猎行为的模拟，通过鲸鱼群体搜索、包围、追捕和攻击猎物等过程实现优时化搜索的目的。在原始的WOA中，提供了包围猎物，螺旋气泡、寻找猎物的数学模型。在初始每个鲸鱼的位置

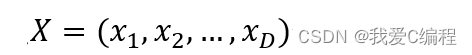
代表了一个可行解，通过后期探索和开发两个阶段，逐步找到最佳位置，即最优解。

首先，座头鲸可以识别猎物的位置并将其包围，但由于最佳位置在搜索空间中不是已的，因此WOA算法假定当前最佳候选解决方案是目标猎物或接近最佳猎物。确定最佳搜索代理后，其他搜索代理将因此尝试更新其对最佳搜索代理的位置。此行为由以下方程式表示：

支持向量机（support vector machines, SVM）是二分类算法，所谓二分类即把具有多个特性（属性）的数据分为两类，目前主流机器学习算法中，神经网络等其他机器学习模型已经能很好完成二分类、多分类，学习和研究SVM，理解SVM背后丰富算法知识，对以后研究其他算法大有裨益；在实现SVM过程中，会综合利用之前介绍的一维搜索、KKT条件、惩罚函数等相关知识。本篇首先通过详解SVM原理，后介绍如何利用python从零实现SVM算法。
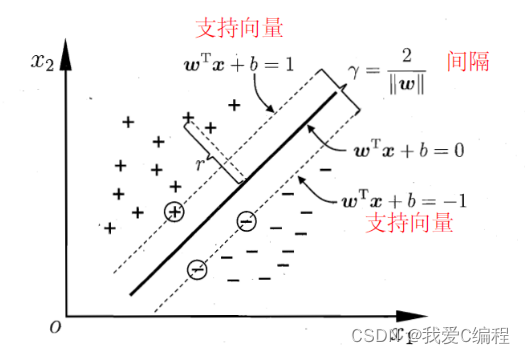
实例中样本明显的分为两类，黑色实心点不妨为类别一，空心圆点可命名为类别二，在实际应用中会把类别数值化，比如类别一用1表示，类别二用-1表示，称数值化后的类别为标签。每个类别分别对应于标签1、还是-1表示没有硬性规定，可以根据自己喜好即可，需要注意的是，由于SVM算法标签也会参与数学运算，这里不能把类别标签设为0。

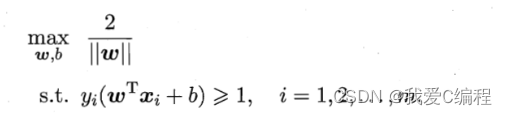
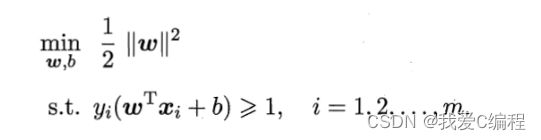
线性核：
主要用于线性可分的情况，我们可以看到特征空间到输入空间的维度是一样的，其参数少速度快，对于线性可分数据，其分类效果很理想
通常首先尝试用线性核函数来做分类，看看效果如何，如果不行再换别的
优点：方案首选、简单、可解释性强：可以轻易知道哪些feature是重要的
缺点：只能解决线性可分的问题

高斯核：

通过调控参数，高斯核实际上具有相当高的灵活性，也是使用最广泛的核函数之一。
如果σ \sigmaσ选得很大的话，高次特征上的权重实际上衰减得非常快，所以实际上（数值上近似一下）相当于一个低维的子空间；
如果σ \sigmaσ选得很小，则可以将任意的数据映射为线性可分——当然，这并不一定是好事，因为随之而来的可能是非常严重的过拟合问题。
优点：可以映射到无限维、决策边界更为多维、只有一个参数
缺点：可解释性差、计算速度慢、容易过拟合

多项式核

多项式核函数可以实现将低维的输入空间映射到高纬的特征空间，
但是多项式核函数的参数多
当多项式的阶数比较高的时候，核矩阵的元素值将趋于无穷大或者无穷小，计算复杂度会大到无法计算。
优点：可解决非线性问题、主观设置
缺点：多参数选择、计算量大
sigmoid核

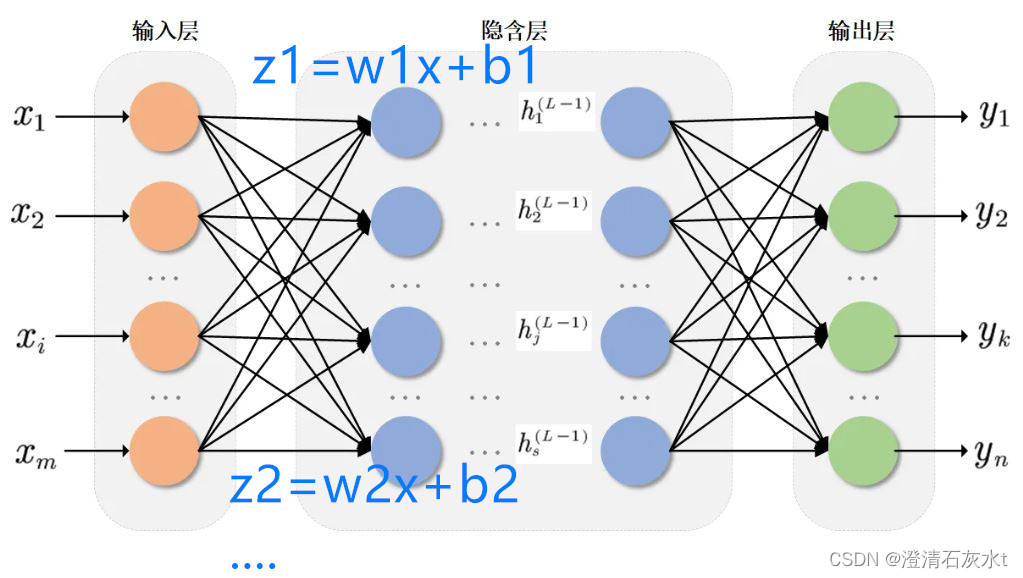
采用sigmoid核函数，支持向量机实现的就是只包含一个隐层，激活函数为 Sigmoid 函数的神经网络。
应用SVM方法，隐含层节点数目(它确定神经网络的结构)、隐含层节点对输入节点的权值都是在设计(训练)的过程中自动确定的。
而且支持向量机的理论基础决定了它最终求得的是全局最优值而不是局部最小值，也保证了它对于未知样本的良好泛化能力而不会出现过学习现象。
如图，输入层->隐藏层之间的权重是每个支撑向量，隐藏层的计算结果是支撑向量和输入向量的内积，隐藏层->输出层之间的权重是支撑向量对应的

woa-svm流程图如下所示：

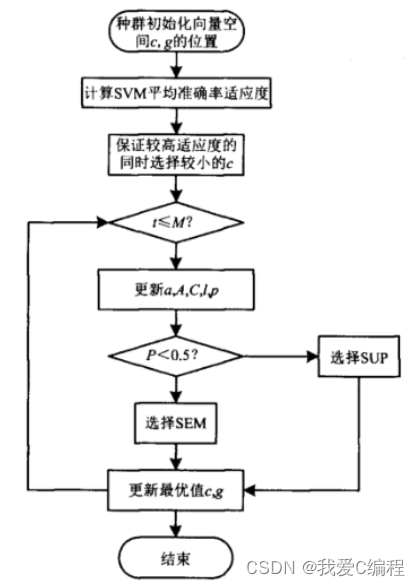
2.仿真效果预览

matlab2022a仿真结果如下：

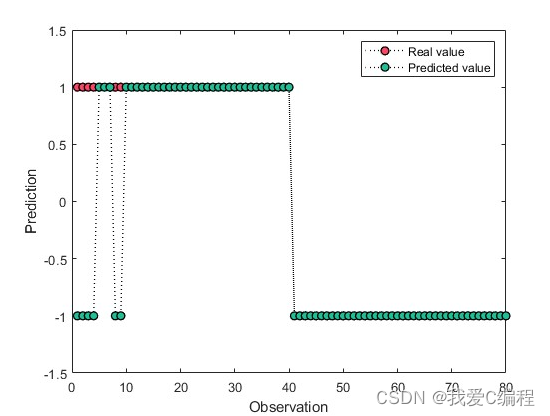
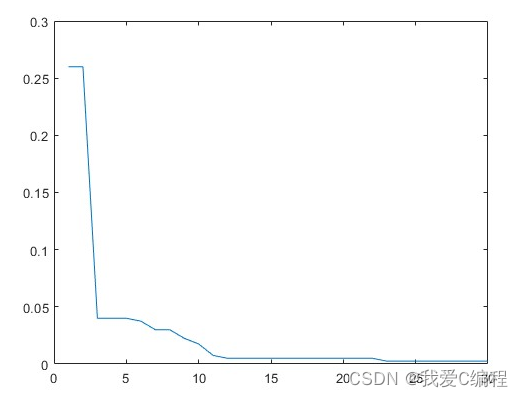
3.MATLAB核心程序

clc;
clear;
close all;
warning off;
addpath(genpath(pwd));
 
global traindata trainlabel
 
% Industrial process data
load ('.\data\data_2.mat')
 
% Parameter setting of WOA
agent = 10;            % Number of search agents
iteration = 30;        % Maximum numbef of iterations
lb = [10^-3,2^-7];     % Lower bound of 'c' and 'g'
ub = [10^0,2^7];       % Upper bound of 'c' and 'g'
dim = 2;               % Number of Parameter
fobj = @woa_obj;       % Objective function
 
% Parameter optimization using WOA
[Best_score, Best_pos, Convergence_curve] = WOA(agent, iteration, lb, ub, dim, fobj);
 
 
% Train SVDD hypersphere using the optimal parameters
cmd = ['-s 5 -t 2 ', '-c ', num2str(Best_pos(1,1)), ' -g ', ...
    num2str(Best_pos(1,2)), ' -q'];
model = libsvmtrain(trainlabel, traindata, cmd);
 
% Test 
[predictlabel, accuracy, ~] = libsvmpredict(testlabel, testdata, model);
 
% Visualize the results
plotResult(testlabel,predictlabel)
 
 
figure
plot(Convergence_curve);

SVM采用的libsvm工具箱，通过测试，在matlab2022a中可以正常运行。

function obj = woa_obj(para)
 
 
global traindata trainlabel
 
c = para(1,1);
 
g = para(1,2);
 
 
cmd = ['-s 5 -t 2 ', '-c ',num2str(c), ' -g ', num2str(g), ' -q'];
 
 
model = libsvmtrain(trainlabel, traindata, cmd); 
 
[~, acc, ~] = libsvmpredict(trainlabel, traindata, model);
 
obj = 1-acc(1,1)/100;
end
A142