活动 - AcWing + 算法竞赛进阶指南
一、迭代加深概述
dfs每次选定一个分支,直到抵达递归边界才回溯,这种策略有一定缺陷。当搜索树的某个分支情况非常多,并且问题的答案在一个较浅的分支上时,如果一开始就选错了分支,那么就会在没有答案的子树上浪费很多时间。
因此我们可以从小到大限制搜索的深度,如果在当前深度限制下搜不到答案,就把深度限制增加,重新搜索。这就是迭代加深的思想。
迭代就是以上次的结果为基础,重复执行以逼近答案的意思。
总之,当搜索树的规模随着层次的深入增长很快,并且我们能够确保答案在一个较浅层的节点时,就可以采用迭代加深dfs。
二、例题:acwing170加成序列

主要信息:
- 开始是1,结尾是指定的n
- 严格递增
- 必须满足是第k个数是前面某两个数相加可得到,这两个数可以是同一个数
可以推算,因为n小于100,加成序列的长度不会很长(2的次方逼近),因此考虑迭代加深算法。
直觉做法:大框架:设定迭代加深深度depth即序列长度,从1开始,不行就++。对每个depth深搜一次,True了就停止然后输出序列。
搜索框架:从小到大枚举序列的位置,对第k个数,枚举前面的位置i,j(i,j可以相等),得出第k个数所有的可能取值s。然后搜索下一个位置。当位置大于depth时返回false,当当前位置选了n时返回true
细节处理:对于可能取值s,要求s递增,s不能重复,s小于n
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N =110;
int n;
int path[N];
bool dfs(int u,int depth)
{
if(u>depth) return false;
if(path[u-1]==n) return true;
bool st[N]={0};
for(int i=u-1;i>=0;i--)
for(int j=i;j>=0;j--)
{
int s=path[i]+path[j];
if(s>n||st[s]||s<=path[u-1]) continue;
st[s]=true;
path[u]=s;
if(dfs(u+1,depth)) return true; //不需要恢复现场因为bool数组是局部变量
}
return false;
}
int main()
{
path[0]=1;
while(cin>>n,n)
{
int depth=1;
while(!dfs(1,depth)) depth++;
for(int i=0;i<depth;i++) cout<<path[i]<<" ";
cout<<endl;
}
return 0;
}
作者:yankai
链接:https://www.acwing.com/activity/content/code/content/4231905/
来源:AcWing
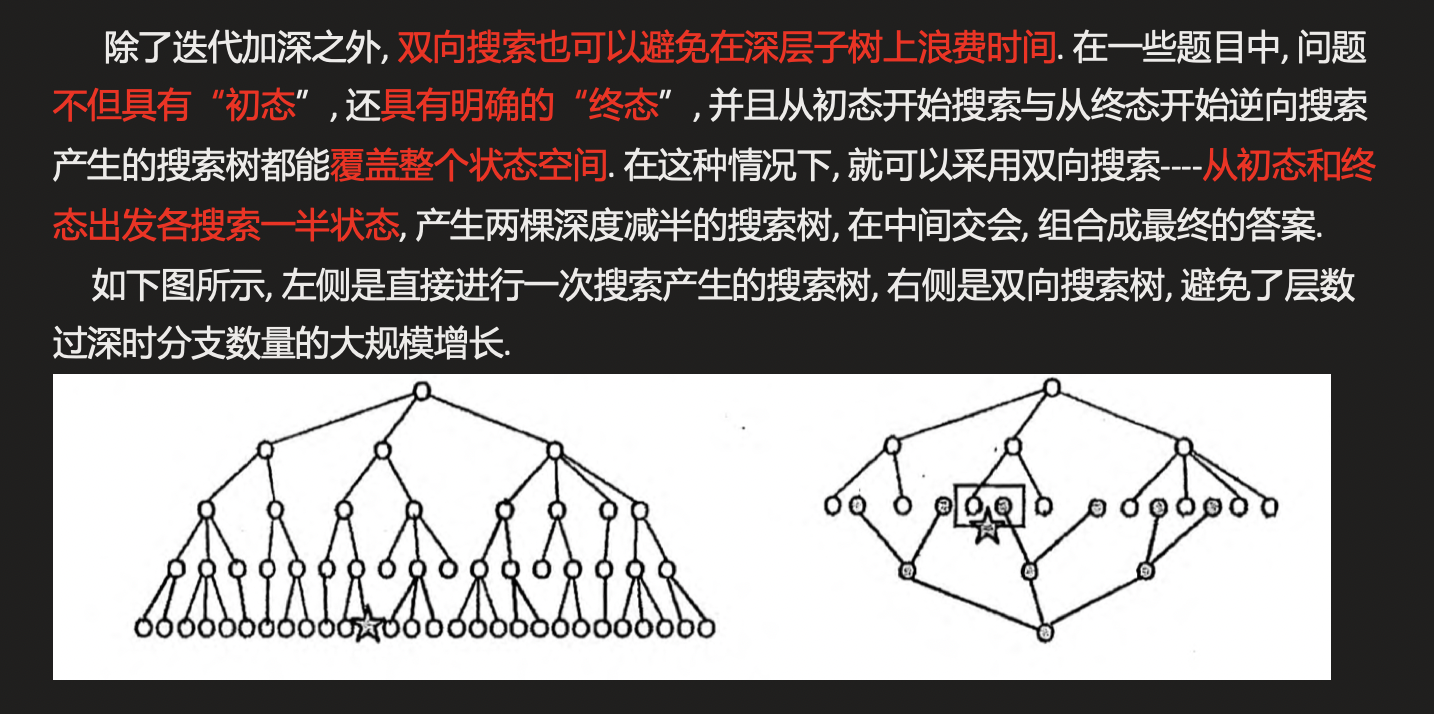
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。三、双向dfs概述
图片来自:AcWing 171. 送礼物 - AcWing
四、双向dfs例题:

题目意思:从N个数中选几个数,使得结果最接近W但不大与W。可以用背包问题求解,但是这里Gi太大了,做不了。
考虑搜索算法,最直接的算法就是直接枚举每个物品选或者不选,那么就有2^46种状态,复杂度过高。这时我们就可以考虑用双向dfs将搜索树分成两半。
首先我们先从前一半礼物中选出若干个,可能达到的0~W之间的所有重量记录在A中,然后对A进行排序、去重
然后尝试从后一半礼物中选出一些,对于买个可能的重量值t,在第一部分的A数组中二分查找小于等于W-t的最大的一个数,用他们的和更新答案。
这个算法的复杂度就是只有O(2^{N/2}log2^{N/2})。
还可以加入一些之前提过的优化提高算法效率:
1.优化搜索顺序,先把礼物按重量降序排序,分半
2.选取合适的折半搜索点。。因为二次搜索需要在第一次搜索中得到的数组进行二分查找,效率相对较低。因此我们应该稍微增加第一次搜索的礼物数,减少第二次搜索的礼物数。经过测试,取第1~N/2+2个礼物为“前一半”时搜索速度最快。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N =50;
typedef long long LL;
int n,m,k;
int w[N];
int weights[1<<24],cnt=0;
int ans;
void dfs1(int u,int s)
{
if(u==k)
{
weights[cnt++]=s;
return;
}
if((LL)s+w[u]<=m) dfs1(u+1,s+w[u]);
dfs1(u+1,s);
}
void dfs2(int u,int s)
{
if(u==n)
{
int l=0,r=cnt-1;
while(l<r)
{
int mid=l+r+1>>1;
if(weights[mid]+(LL)s<=m) l=mid;
else r=mid-1;
}
if(weights[l]+(LL)s<=m) ans=max(ans,weights[l]+s);
return;
}
if((LL)s+w[u]<=m) dfs2(u+1,s+w[u]);
dfs2(u+1,s);
}
int main()
{
cin>>m>>n;
for(int i=0;i<n;i++) cin>>w[i];
sort(w,w+n);
reverse(w,w+n);
k=n/2;
dfs1(0,0);
sort(weights,weights+cnt);
int t=1;
for(int i=1;i<cnt;i++)
if(weights[i]!=weights[i-1])
weights[t++]=weights[i];
cnt=t;
dfs2(k,0);
cout<<ans<<endl;
return 0;
}