目录
一、控制系统
1.1控制系统的分类
1.2 性能指标
二、PID算法的起源及特点
三、PID应用
四、PID公式原理
五、PID源码
六、PID整定方法
6.1 经验法
6.2 衰减曲线法
6.3 响应曲线法
参考文献:
一、控制系统
1.1控制系统的分类
分为开环控制、闭环控制和复合控制
1.1.1开环控制:系统输出的量不会对系统的控制输入量有反馈,可分为二/三位式控制、多位式控制;
二/三位式控制指的是控制输入的量为两个或三个状态,例如加热系统的开和关两个控制动作,当开启加热到达指定温度范围时,关闭加热控制。或者加热系统的控制有3个档位调节,全功率、半功率、关等3个输入控制操作。
多位式控制指的是输入控制量可以为多个输入量,例如输入不同的固定PWM占空比给电机,则电机执行不同的转速,虽然刚开始电机的转速为某个值,但是随着时间的运行,电机受热或者环境因素、负载等的影响,电机受到扰动导致转速发生变化。
分为给定量控制和按照扰动控制:
按照给定量进行控制:给定输入量产生对应的输出量,受到扰动干扰明显

开环控制系统框图
按照扰动控制:给定输入会产生对应输出量,但是输出量会动态调整,即是系统直接从扰动处获取信息并以此改变控制量来达到动态适应扰动效果,具有控制精度高,但只适用于扰动可测量情况。

开环扰动控制系统框图
开环控制的问题是:受到扰动因素影响较大,无法自动修正偏差,抗扰动性差,控制系统的输出在设置的定值附近波动,系统输出不能很好的跟踪在设定值的很小偏差范围内。其控制精度完全取决于所用器件、校准的精度以及系统的扰动的程度。
1.1.2 闭环控制:也即是反馈控制,控制系统的输出量会反馈给设定值,两者的差值大小判断以动态的调整控制量来实现系统输出量和设定值接近。也即是反馈控制是按照偏差大小进行控制,也即是当系统内外扰动量导致系统输出量偏离设定值(期望值)而出现偏差时,会有一个反馈控制量去减少该偏差使得系统的输出量和设定值趋于一致。
闭环相比开环控制的优势:控制的精度高

闭环控制系统框图
其中的反馈量也称为过程变量
1.1.3 复合控制
复合控制方式为:按扰动控制和按偏差控制(反馈控制)结合
1.2 性能指标
衡量控制系统性能好坏的标准是:快、准、稳。
稳定性:被控量经过过渡过程后,其在设定值附近的振荡过程逐渐减弱,则最终系统会达到平衡状态,则称系统为稳定系统,反之若振荡过程逐渐加强,则系统为不稳定系统
也表述为控制系统对干扰和非线性的耐受程度,在某些情况下存在干扰或系统的非线性导致控制系统的输出量无法给出期望的响应。
准确性:稳态误差指标,一般要求:稳态误差小,也即是被控量达到稳定状态时的值和设定的值偏差很小
快速性:过渡时间和超调量指标,一般要求:过渡时间短,超调量小
上升时间、过冲百分比、稳定时间、稳定状态误差、死区(不响应期)、循环周期
上升时间:给定阶跃信号,系统从稳态的10%上升到设定值的90%所需时间
超调量(过冲百分比):给定阶跃信号,被控量超出设定值的百分比
稳定时间:给定阶跃信号,被控量(输出量)从初始时刻稳定到设定值范围内(5%)所需时间
死区(不响应期):给定阶跃信号,控制系统不会立即响应,其输出量不会有变化,从给定动作信号开始到控制系统有响应的这段时间为死区时间
循环周期(控制周期、采样周期):调用控制算法的时间间隔,也即是多久执行一次控制。
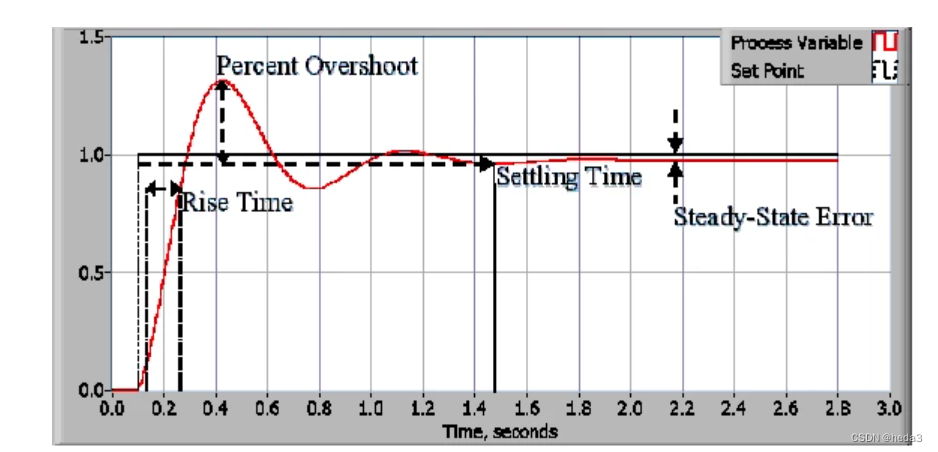
引用1该图片说明了:上升时间(Rise Time)、超调量(Percent Overshoot)、稳态时间(Setting Time)、稳态误差(Steady-State Error)上述标注的过程变量Process Variable(也称为反馈量、输出量)

引用1该图片说明了:死区时间(DeadTime)
二、PID算法的起源及特点
PID算法起源:
1、公元前我国古代自动计时器、漏壶指南车
2、1788年瓦特蒸汽机的离心式调速器
3、1868年麦克斯韦研究反馈系统的稳定性问题、发表轮调速器论文
4、1892年,俄国李雅普诺夫提出李雅普诺夫稳定性理论
5、20世纪10年代,PID控制器出现
6、1927年,反馈放大器出现(为解决电子管在性能发生较大变化时依然能工作)
7、1945年,贝塔朗菲提出《系统论》
8、1948年,维纳提出《控制论》--形成了完整的控制理论体系--以传递函数为基础的经典控制理论(主要研究单输入单输出、线性定常系统的分析和设计问题)
PID算法属于反馈控制,特点:算法简单、鲁棒性好、可靠性高。
PID算法种类:
1、位置PID
2、增量PID
3、积分分离PID
4、抗积分饱和PID
5、梯形积分PID
6、变速积分PID
7、不完全微分PID
8、微分先行PID
9、带滤波器的PID
10、带死区的PID
三、PID应用
过程控制:温度、流量、压力、液位等控制
例如:锅炉温度控制、流量控制器等
运动控制:速度、位置等控制
例如:车辆运动控制、磁盘的读写头定位、数控机床控制等
四、PID公式原理

PID控制器:将偏差量的比例(P-Proportion)、积分(I-Integral)、微分(D-Differential)按照线性组合构成控制量,从而对被控对象进行控制
Uout=Pout+Iout+Dout
连续系统的PID控制规律表述为:
(1)
也即是:
令
则上述的(1)式可表述为:
--(2)式
--(3) 式
离散的PID控制规律为:
对(3)式进行离散化处理
用过去一段时间采样点的偏差值的代数和代替积分。
上述的kT表示第k个采样点时间,k取值范围为0,1,2...
--(4) 式
简化形式为:其中的kT用k表示
且error用e替代
最终得到化简公式5:
--(5)式
该式称为位置式PID,该控制器的输出u(k)可直接驱动执行机构。对比增量式PID。
需依据实际的控制系统设定和调节的参数为:
1)采样周期T(也称控制周期,每隔T时间进行一次PID计算)
2)比例系数Kp、积分系数Ki、微分系数Kd (PID整定)
五、PID源码
上述的位置PID控制的公式进行程序编写:
/*PID结构体*/
typedef struct
{
float SetValue; //设定值
float ActualValue; //实际值
float Kp; //比例系数
float ki; //积分系数
float kd; //微分系数
float T; //采样周期
float kpout; //比例输出控制量
float kiout; //积分输出控制量
float kdout; //微分输出控制量
float ek; //当前偏差
float ek1; //上一次偏差
float ek2; //上上次偏差
float Out; //输出控制量
}PID;当时间到达采样周期T时,执行一次PID_C函数
void PID_C(PID *PID, float ActualValue)
{
//当前偏差
PID->ek=PID->SetValue-ActualValue;
//比例输出控制量
PID->kpout=PID->kp*PID->ek;
//积分输出控制量
PID->kiout+=PID->ek;
PID->kiout*=PID->ki;
//微分输出控制量
PID->kdout=PID->kd*(PID->ek-PID->ek1);
//PID控制器的输出控制量
PID->out=PID->kpout+PID->kiout+PID->kdout;
//历史偏差量赋值
PID->ek1=PID->ek;
}六、PID整定方法
对于一般的控制系统,通过调节kp、ki、kd参数可实现控制系统按照期望的设定值去产生相应的动作。也即是通过该参数的整定来逼近控制器模型。
工程上常用的整定方法:
1、经验法
2、衰减曲线法
3、响应曲线法
6.1 经验法
比例控制,比例系数调小,则调节的力度不够,系统输出量变化缓慢;比例系数调大,则调节速度变快,若调节力度太强,则系统的输出量变化快速使得系统输出来回振荡,调节时间加长,若太大则使得闭环系统不稳定;
积分控制,误差e(i)为负时(误差为设定值减去实测值,说明实测值高于设定值),对应的积分增加量为负,也即是积分控制输出量减小以实现实测值往设定值方向逼近(目的让实测值往大的方向接近设定值)。当误差为正时(实测值低于设定值),对应的积分增加量为正,也即是积分控制输出量增大以实现实测值往设定值方向逼近(目的让实测值往大的方向接近设定值)。其中的积分调节只要误差e(i)不为零,控制器的输出控制量会因为积分作用不断变化,积分控制作用:消除稳态误差、提高控制精度。从上述的位置PID公式可看出积分项为历史误差的累积,因此当系统发生扰动变化时,该积分控制具有较大的滞后。当ki设置大时,由于累积作用使得超调量增大
微分控制,当前误差和上一次误差的差值和微分系数的乘积,其中当前误差和上一次误差的差值表示误差的变化速率,误差变化速率越快,则微分的绝对值越大。
1)当e(k)-e(k-1)大于零,且 当e(k)大于零时(设定值大于实测值),说明实测值正在偏离设定值(且当前的实测值小于设定值),此时微分控制量
为正,使得实测值往设定值方向逼近;
2)当e(k)-e(k-1)大于零,且e(k)小于零时(设定值小于实测值),说明实测值正在接近设定值(且当前实测值大于设定值),此时微分控制量为正,抑制控制量过调。
3)当e(k)-e(k-1)小于零,且当e(k)大于零时(设定值大于实测值),说明实测值正在接近设定值(且当前实测值小于设定值),此时微分控制量为负,抑制控制量过调;
4)当e(k)-e(k-1)小于零,且当e(k)小于零时(设定值小于实测值),说明实测值正在远离设定值(且当前实测值大于设定值)此时微分控制量为负,使得实测值往设定值方向逼近。
从微分的上述控制过程可看出,微分控制具有超前和预测特性,在超调未出现之前能提前给出控制作用,缺点:对干扰噪声敏感,使得系统抑制干扰能力降低。
在调试Kp、ki、kd系数的过程中,以超调量、稳态误差以及上升时间等为衡量参数整定的性能。
若超调量过大,则应减少kp,减小ki(增大积分时间);若被控量上升缓慢(过渡时间太长)则应增加kp,增加ki(减少积分时间),若消除误差的速度慢则应增加ki(减少积分时间);若加入kp和ki后超调量很大或者依然不满足要求则可以加入kd,kd从小到大,并反复微调kp、ki和kd参数。
其它调试经验参考:
引用自博文[3]
引用自博文[3]
业界流传的:
参数整定找最佳,从小到大顺序查
先是比例后积分,最后再把微分加
曲线振荡很频繁,比例度盘要放大
曲线漂浮绕大湾,比例度盘往小扳
曲线偏离回复慢,积分时间往下降
曲线波动周期长,积分时间再加长
曲线振荡频率快,先把微分降下来
动差大来波动慢。微分时间应加长
理想曲线两个波,前高后低4比1
一看二调多分析,调节质量不会低
其中的比例度=
6.2 衰减曲线法
应用场景:被控系统具有自平衡能力
1)先采用比例控制,从较小的比例系数kp开始,逐步增加比例系数,使得系统对阶跃输入的响应达到临界状态,记录此时kp,临界振荡周期记作Tr,如下图所示

2)依据Ziegler-Nichols的临界比例度经验公式确定PID控制参数
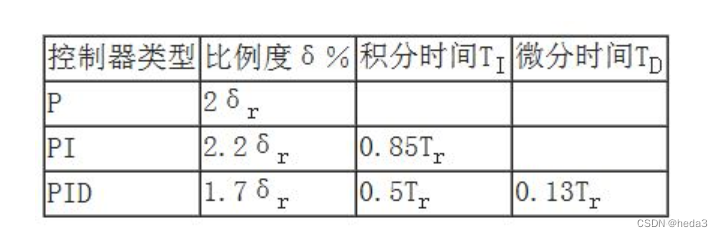
其中的比例度和比例系数的关系为:
比例度=
6.3 响应曲线法
依据给定对象的瞬态响应特性参数K、T、来确定PID控制器的参数
例如带有时滞环节的一阶模型:
操作步骤:
1)开环控制,给定阶跃输入信号
2)记录被控对象的输出特性曲线,如图2-1所示
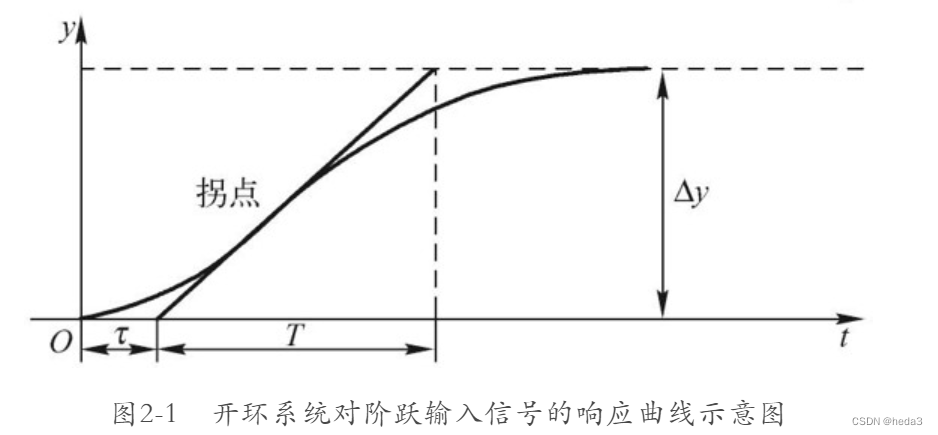
3)从曲线上求得参数umin、umax、ymin、ymax、T和
其中的umin、umax为输入信号的最小和最大值,为输入信号的阶跃值,ymin、ymax为输出的最小和最大值
4)计算K和

5)按照求得的参数依据下表查找对应的PID控制参数
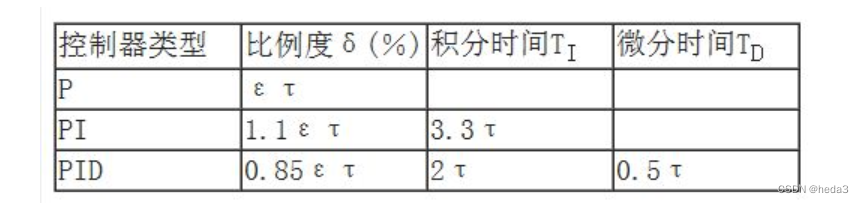
其中的比例度和比例系数的关系为:
比例度=
参考文献:
【1】PID理论详解 - NI
【2】自动控制原理
【3】PID控制详解_tingfenghanlei的博客-CSDN博客_pid控制
【4】一文搞懂PID控制算法_不脱发的程序猿的博客-CSDN博客_pid控制
【5】一文读懂PID控制算法(抛弃公式,从原理上真正理解PID控制)_确定有穷自动机的博客-CSDN博客_pid