1.算法描述

涡旋光束是一种具有螺旋波前的光束，在涡旋光束中，决定涡旋光束特性的角量子数可以是任意一个自然数，其不同设置所产生的涡旋光束之间存在正交关系。目前，产生涡旋光束的方式很多种，总的来讲，包括腔外光束产生方式和腔内光束产生方式两种类型。第一种产生方式，其主要通过谐振器件来得到髙斯光束，然后将高斯光束通过特殊的相位元件来达到空间整形的目的，继而产生相应的涡旋光束。第二种产生方式，其直接进行空间相位整形，并在谐振腔内得到相应的涡旋光束。第二种产生方式也就是常见的涡旋激光器。目前为止，涡旋光束有着极其广泛的应用前景，包括生物医学领域，原子物理学领域，材料科技以及激光等多个领域。

但是涡旋光束在大气中传输的时候，由于受到各种大气因素的干扰，如光线干扰，天气影响，气温压强变化，从而导致大气折射率的改变。此时，涡旋光束在传输过程中会受到大气折射率的影响，从而导致涡旋光束在大气传播时，出现诸如光束扩展、光束抖动、涡旋光束的OAM谱弥散，串扰等问题，即大气湍流效应[02,03] 。

因此，对受到大气湍流影响的涡旋光束进行校正就显得格外重要，传统的光学校正，其工作流程主要分为五个步骤。

第一、涡旋光束受到大气湍流的影响而导致了相位的畸变、串扰等问题。

第二、相位畸变和串扰等影响了通信质量；

第三、加入自适应光学校正模块，得到预校正的涡旋光束，控制相位和光强分布；

第四、自适应光学校正模块减少了涡旋光束的相位的畸变、串扰等问题。

第五、改善通信指标，提升了通信性能。

但由于涡旋光束有其特殊的相位特性和光强度分布特性，使得传统的光学校正方法无法达到校正效果，因此研究一种适用于受到大气湍流影响的涡旋光束的自适应校正技术具有十分重要的意义。

涡旋光束是一种具有OMA轨道角动量的激光光束，其相位呈现为螺旋分布状态，但光束中心处的相位是未知的。Allen等人提出了涡旋光束的相位可以通过如下公式表示：

涡旋光束有多种表现形式，如贝塞尔光束，拉盖尔-高斯光束以及环形涡旋光束等。其中环形涡旋光束是以高斯光束为基础实现的，其计算表达式为：

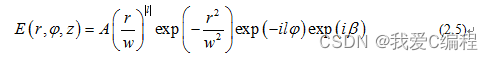
贝塞尔光束中包含贝塞尔函数，他是一种空心光束，贝塞尔光束属于一种经典的涡旋光束。其表达式为：

大气湍流的基本原理最早是由Kolmogorov在二十世纪四十年代提出的，在其原理中提供通过大雷诺兹数来表示湍流的内部结构，从而推进了湍流理论的发展，因此基于大雷诺兹数的湍流理论奠定了现代湍流理论的基础[13]。

在Kolmogorov的湍流理论中的相关定义可知，流体具有层流和湍流两种不同的状态。其中，当流体运行速度较低的时候，流体的流线比较平滑，因此流体处于层流状态。而当流体运行速度较大的时候，流体的流线将变得随机不规则，那么这种状态就是流体的湍流。层流和湍流的示意图如下图所示：

由Kolmogorov的湍流理论可知，大气湍流情况和流体湍流类似，两者不同之处在于其物理性质不同，由于受到光线干扰，天气影响，气温压强变化等因素的影响，大气一直处于流动状态，从而产生不同压强、流速、气压的旋涡，如图2.4所示。然后多个旋涡相互影响，相互关联和重叠，共同作用下产生了大气湍流现象。大气湍流会导致折射率的改变。因此，涡旋光束在大气中传输会受到大气折射率的影响，从而导致涡旋光束的光束扩展、光束抖动、OAM谱弥散，串扰等问题。

涡旋光束在大气湍流中传输时，光束将发生波前畸变，随后涡旋光束的光强度将呈现非均匀分布，明暗度不一，光斑的外形将发生严重扭曲并且目标的OAM能量占比将明显下降。因此需要对畸变的光束进行校正，使得光强分布变得均匀，光斑的外形将得到进一步规整，并且目标的OAM能量占比将得以提高。

2.仿真效果预览

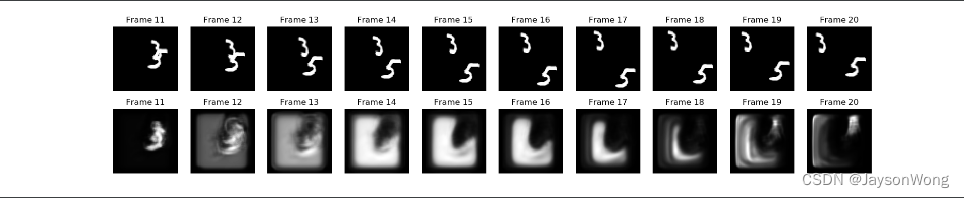
matlab2022a仿真结果如下：

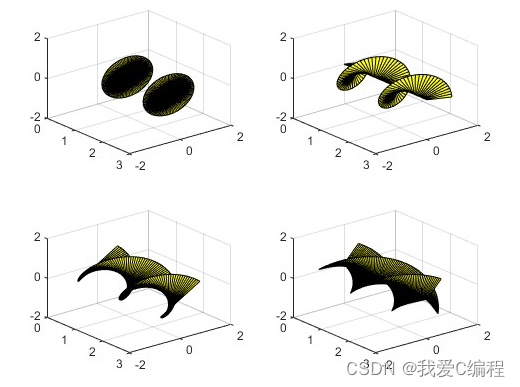
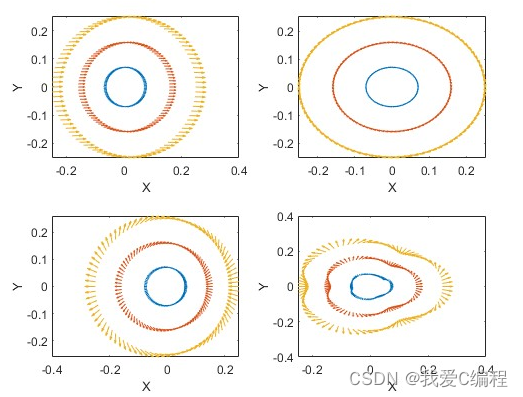
从图仿真结果可知，随着传输距离的不断增加，涡旋光束通过有湍流传输之后，其光强度分布随着传输距离的增加而不断分散，相位相位的“每一扇叶片”的分界处随着传输距离的变得更加模糊。而通过自适应校正之后，涡旋光束的强度和相位均得到了有效的校正。其光强度分布更叫均匀，但是在相位跳变区域，随着距离的增加，通过自适应校正后仍存在一定的影响。

3.MATLAB核心程序

 
 
%%
%大气湍流的物理特性分析
Dist = [0:2000:20000];
 
figure;
indx = 0;
rad1 = [];
for L=Dist
    indx      = indx + 1;
    Cn        = 8*10^(-9); 
    th        = 4.03*Cn.^(6/5)*0.6328.^(-1/5)*L.^(3/5); 
    rad1(indx)= th*L; 
end 
plot(Dist,rad1,'b-o')  
% title('涡旋光束光斑尺度和传输距离的关系') 
xlabel('传输距离') 
ylabel('涡旋光束光斑尺度') 
 
figure;
indx = 0;
rad2 = [];
Cset = [0:20*10^(-9):500*10^(-9)];
for Cn = Cset
    indx       = indx + 1;
    L          = 100; 
    th         = 4.03*Cn.^(6/5)*0.6328.^(-1/5)*L.^(3/5); 
    rad2(indx) = th*L; 
end 
plot(Cset,rad2,'b-o') 
% title('涡旋光束光斑尺度和湍流强度的关系') 
xlabel('湍流强度') 
ylabel('涡旋光束光斑尺度') 
 
 
figure;
indx = 0;
alf  = [];
Dist = [0:2000:20000];
for L= Dist 
    indx      = indx + 1;
    Cn        = 8*10^(-9); 
    alf(indx) = sqrt(1.75*Cn*Cn*L*3.2^(-1/3)*10^(-18)); 
end 
plot(Dist,alf,'b-o') 
% title('涡旋光束光斑偏移角度和传输距离的关系') 
xlabel('传输距离') 
ylabel('涡旋光束光斑偏移角度') 
 
figure;
indx = 0;
Cset = [0:20*10^(-9):500*10^(-9)];
alf  = [];
for Cn=Cset 
    indx      = indx + 1;
    L         = 1000; 
    alf(indx) = sqrt(1.75*Cn*Cn*L*3.2^(-1/3)*10^(-18)); 
end 
plot(Cset,alf,'b-o') 
xlabel('湍流强度') 
ylabel('涡旋光束光斑偏移角度') 
 
figure;
indx = 0;
B    = 0.49;
Dist = [0:500:20000];
I    = [];
for  L=Dist 
     indx   = indx + 1;
     Cn     = 8*10^(-9); 
     I(indx)= B*(2*pi/0.6328).^(7/6)*L.^(11)*Cn.^2*10^(-18); 
end 
plot(Dist,I,'b-o') 
xlabel('传输距离') 
ylabel('涡旋光束光强起伏')
 
figure;
indx = 0;
B    = 0.49; 
Cset = [0:20*10^(-9):500*10^(-9)];
I    = [];
for Cn=Cset
    indx   = indx + 1;
    L      = 1000; 
    I(indx)= B*(2*pi/0.6328).^(7/6)*L.^(11)*Cn.^2*10^(-18); 
end 
plot(Cset,I,'b-o') 
xlabel('湍流强度') 
ylabel('涡旋光束光强起伏') 
 
%%
%光线通过大气湍流的变换仿真分析
N         = 300;
w0        = 0.03;
s         = 5;
z         = 1000;
lamda     = 1.550e-6;
k         = 2*pi/lamda;
z0        = k*w0^2/2;
%图像坐标范围
b         = 0.2;
dx        = b/N;
Cn2       = 1e-15;
%传输距离
Numz      = 20;%把传播距离分成Numz段
dz        = z/Numz;%每段的距离
m2        = [-N/2:N/2-1];
[r,theta] = meshgrid(linspace(0,b,N),linspace(0,2*pi,N));
[x,y]     = pol2cart(theta,r);
%窗口宽度
L         = 0.7;
df        = 1/L;
%空间频率
[fx,fy]   = meshgrid(m2*df);
fr        = sqrt(fx.^2+fy.^2);
kx        = 2*pi*fx;
ky        = 2*pi*fy;
kr        = 2*pi*fr;
A         = sqrt(2/(pi*gamma(abs(s)+1)));
%发射光束的表达式
u0        = A*exp(-r.^2/w0^2).*(sqrt(2)*r/w0).^s.*exp(1i*s*theta);
u         = u0;
phi       = func_influence(lamda,z,Cn2);
for j=1:Numz
      u1 = fft2(exp(1i*phi).*u);
      u1 = fftshift(u1);
      u  = ifft2(ifftshift(exp(1i*k*dz)*exp(-1i*dz*kr.^2/(2*k)).*u1));
end
 
%强度和相位图
[X,Y] = meshgrid(m2*dx);
uz    = griddata(x,y,u,X,Y);
A141