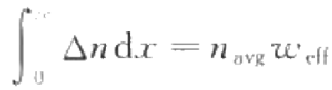文章目录
- 正规文法
- 正规式
- 有穷自动机
- 确定的有穷自动机——DFA
- 不确定的有穷自动机——NFA
- DFA 与 NFA 的区分
- 正规式转换为正规文法
- 正规文法转换为正规式
- NFA 转换为 DFA
- NFA 最小化
- NFA 转换为正规式
- 正规式转换为 NFA
- 正规文法转换为 NFA
- NFA 转换为正规文法
前言:
在学习正规文法之前,需要先了解一下什么是文法,具体可以查看这篇文章,总结的比较好 —— 编译原理–四种文法的理解
正规文法
设有 G=(VN,VT,P,S),若 P 中的每一个产生式的形式都是 A ——> aB 或 A——>a,其中 A 和 B 都是非终结符,a 属于 VT*,则称 G 为 3 型文法,又称正规文法。
正规式
正规式也称正则表达式,也是表示正规集的工具。是一种用于匹配文本模式的字符序列。由普通字符(如字母、数字)和特殊字符(如元字符)组成的表达式。
在正规式中,常见的元字符包括:
-
通配符(如
.表示匹配任意字符) -
字符类(如
[0-9]表示匹配数字0到9之间的任意一个字符) -
量词(如
*表示匹配前面的字符0次或多次) -
锚点(如
^表示匹配字符串的开头、$表示匹配字符串的结尾) -
…
有穷自动机
有穷自动机(Finite State Machine,FSM)是一种抽象的识别装置,用于描述具有有限个状态并在输入序列驱动下进行状态转换的系统,能准确地识别正规集。
一个有穷自动机由以下几个要素组成:
1. 状态集合(States): 有穷自动机的所有可能状态的集合。每个状态代表系统的某种特定情况或条件。
2. 输入字母表(Input Alphabet): 有穷自动机接受的输入符号的集合。例如,二进制数的有穷自动机的输入字母表可以是{0, 1}。
3. 转移函数(Transition Function): 描述从一个状态到另一个状态的转移规则。该函数接受当前状态和输入符号,并返回下一个状态。转移函数可以用图形表示,其中状态是节点,输入符号是边。
4. 初始状态(Initial State): 有穷自动机开始运行时的起始状态。
5. 终止状态(Accepting States): 有穷自动机在运行过程中达到的特殊状态。当有穷自动机达到终止状态时,它可以接受或拒绝输入序列。
有穷自动机分为确定性有穷自动机(Deterministic Finite Automaton,DFA)和非确定性有穷自动机(Nondeterministic Finite Automaton,NFA)。
在确定性有穷自动机(DFA)中,每个状态都有唯一的转移路径,而在非确定性有穷自动机(NFA)中,一个状态可以有多个转移路径。
确定的有穷自动机——DFA
一个确定的有穷自动机 DFA 由一个五元组组成,可以用以下公式表示:
其中:
-
K表示一个有穷集,它的每个元素称为一个状态。 -
Σ表示有穷字母表,Σ = {a₁, a₂, ..., aₘ},每个字母代表有穷自动机接受的输入符号,也成为输入符号表。 -
f表示转移函数,K × Σ → K,它描述从一个状态到另一个状态的转移规则。对于给定的状态Kᵢ和输入符号a,则经过f转换函数后,会返回下一个状态Kⱼ,转换规则如:f(Kᵢ,a) = Kⱼ。 -
S表示初态集,S ∈ K,它是唯一的一个初态。 -
Z表示终态集,Z ⊆ K,当有穷自动机达到终止状态时,它可以接受或拒绝输入序列,也称为可接受状态或结束状态。
不确定的有穷自动机——NFA
一个不确定的有穷自动机 NFA 同样也是由一个五元组组成,可以用以下公式表示:
其中:
-
K表示一个有穷集,它的每个元素称为一个状态。 -
Σ表示有穷字母表,Σ = {a₁, a₂, ..., aₘ},每个字母代表有穷自动机接受的输入符号,也成为输入符号表。 -
f表示转移函数,K × Σ* → K,表示K的全体子集的映像,即 K × Σ* → 2K,其中 2K 表示K的幂集。 -
S表示初态集,S ⊆ K,表示一个非空初态集。 -
Z表示终态集,Z ⊆ K,表示一个终态集。
当有穷字母表 Σ 中存在 ε 空串时,那么该有穷自动机为 NFA。
DFA 与 NFA 的区分
DFA 和 NFA 的主要区别在于它们的转移函数和转移规则:
转移函数不同
DFA 的转移函数是唯一的,即每个状态和输入符号只对应唯一的下一个状态(同一路径中输入符号必须唯一)。
NFA 的转移函数可以有多个下一个状态,也就是说一个状态可以按照多种选择进行转移。
转移规则不同
DFA 的转移规则相对简单,每个状态在接收到输入符号后只能转移到唯一的下一个状态,从而形成确定的转移路径。
NFA 的转移规则更加复杂,一个状态可以按照多种选择进行转移,从而形成多条可能的转移路径。
因此,DFA 模型的缺点是其在某些情况下需要更多的状态来表示相同的语言,并且难以处理一些复杂的语言。然而,DFA 的优势在于其转移函数和转移规则都明确,因此可以直接实现,易于编程实现和模拟执行。
正规式转换为正规文法
在开始转换之前,我们先来了解一下正规式转换正规文法的公式,一共有三个,如下所示:
当存在正规式产生式 A → xy,则有正规文法:
B → y
当存在正规式产生式 A → x*y,则有正规文法:
A → y
B → xB
B → y
当存在正规式产生式 A → x|y,则有正规文法
B → y
转换示例:
将正规式 r = a(a|d)* 转换为相应的正规文法,转换过程如下所示:

正规文法转换为正规式
正规文法转换为正规式同样有三个公式,如下所示:
当存在正规文法 A → xB 且 B → y,则有正规式 A = xy;
当存在正规文法 A → xA|y,则有正规式 A = x*y;
当存在正规文法 A → x 且 B → y,则有正规式 A = x|y;
转换示例:
现有文法 G[S],其所有产生式如下所示:
S → a
A → aA
A → dA
A → a
A → d
将文法 G[S] 转换为正规式:

NFA 转换为 DFA
这里先来了解将 NFA 转化为接受同样语言的 DFA 的算法,称为子集法。
子集法是一种用于将不确定的有穷自动机(NFA)转换为具有等价性的确定的有穷自动机(DFA)的算法。
在子集法中,我们将每个 DFA 状态表示为 NFA 状态的子集。具体步骤如下:
-
创建 DFA 的初始状态。这个初始状态是由 NFA 的初始状态以及通过
ε转移可以到达的其他状态组成的子集。可以表达为ε-closure(I),其中I为初态,也就是求从初态I开始,经过ε所到达的状态形成的闭包集合。 -
对于新创建的 DFA 状态,遍历每个输入符号(除去
ε空串)。对于每个输入符号,找出从当前 DFA 状态中的任意一个 NFA 状态通过该输入符号可以达到的所有 NFA 状态,并将它们作为新的 DFA 状态的部分。可以表示为move(I,a),从初态I开始,经过a弧所到达状态。
重复第 2 步,直到无法再创建新的 DFA 状态为止。最终得到的每个 DFA 状态都与 NFA 的某个状态集合相对应。
转换示例:
将给出的 NFA-N 状态图,转换为等价的 DFA。

NFA 最小化
在进行最小化(简化)前,需要先进行多余状态检查。检查从该自动机的开始状态出发,任何输入串也不能到达的那个状态,或者从这个状态没有通路到达终态。
在确定有限自动机(DFA)中,最小化是指将给定的 DFA 转换为等价且具有最少状态数量的 DFA。
最小化的目的是简化自动机的结构,减少状态数量,从而提高处理效率和性能。
下面是最小化 DFA 的一种常见方法,称为 Hopcroft 算法:
1.初始化分区: 将 DFA 的状态划分为两个初始分区,即接受状态(终态)和非接受状态(非终态)。
2.对于每个划分:
-
a. 对于每个输入符号,检查该划分中的状态在该输入符号下是否具有相同的转移目标。如果不是,则根据该输入符号将状态进行划分。
-
b. 如果对于某个输入符号的划分发生了变化,重新开始对所有划分进行遍历。
重复步骤 2,直到没有新的划分发生,最终得到的划分即为最小化 DFA 的状态集合。
在 Hopcroft 算法中,通过不断比较状态的转移目标,将具有相同转移目标的状态划分在同一个分区。这样可以逐步减少分区的数量,直至无法再进行划分为止。
最小化示例
对上方转换的 DFA 状态图进行最小化处理。

NFA 转换为正规式
将 NFA 转换为具有等价性的正规式公式如下:

转换示例:
正规式转换为 NFA
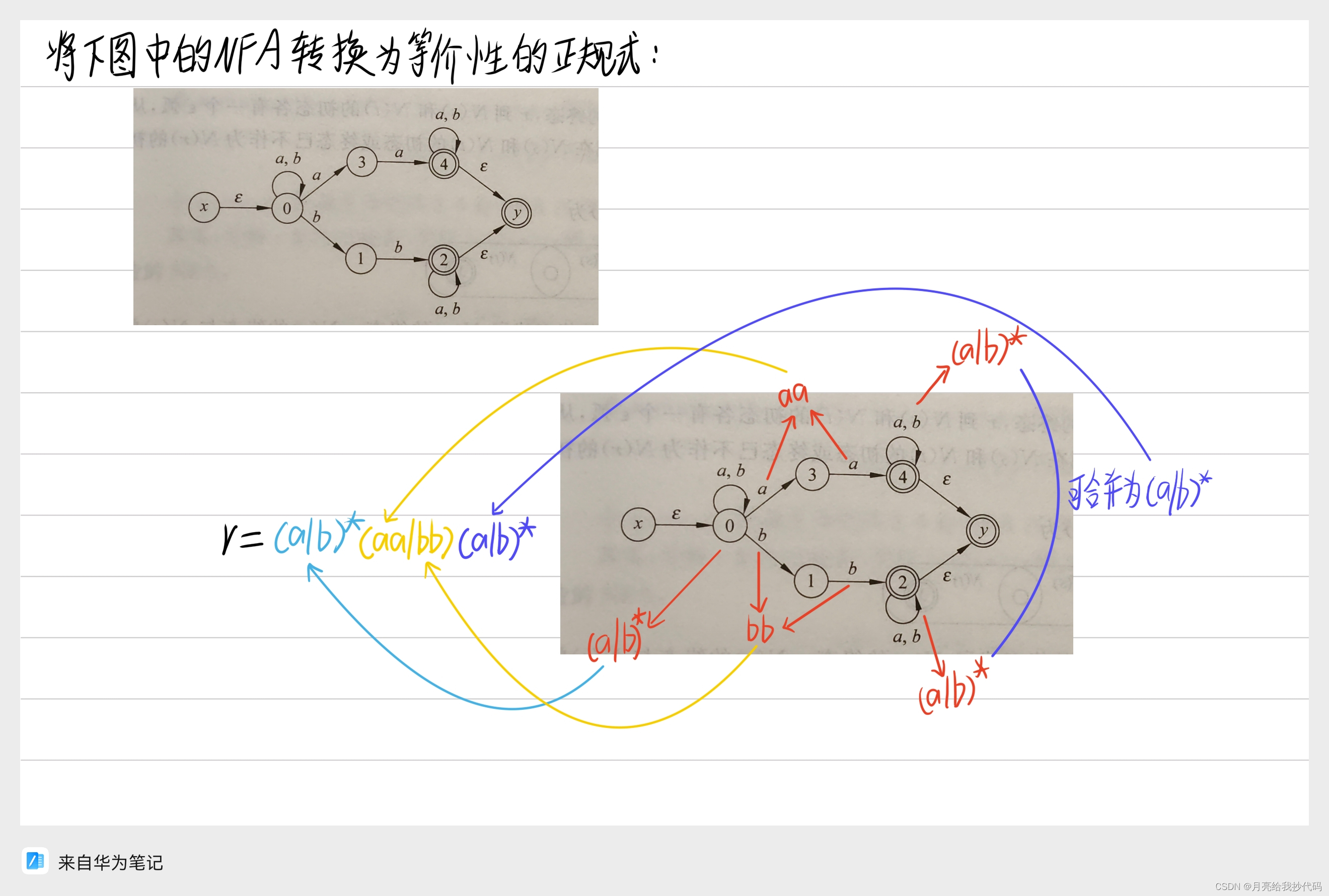
将正规式转换为具有等价性的 NFA 公式如下:
转换示例:

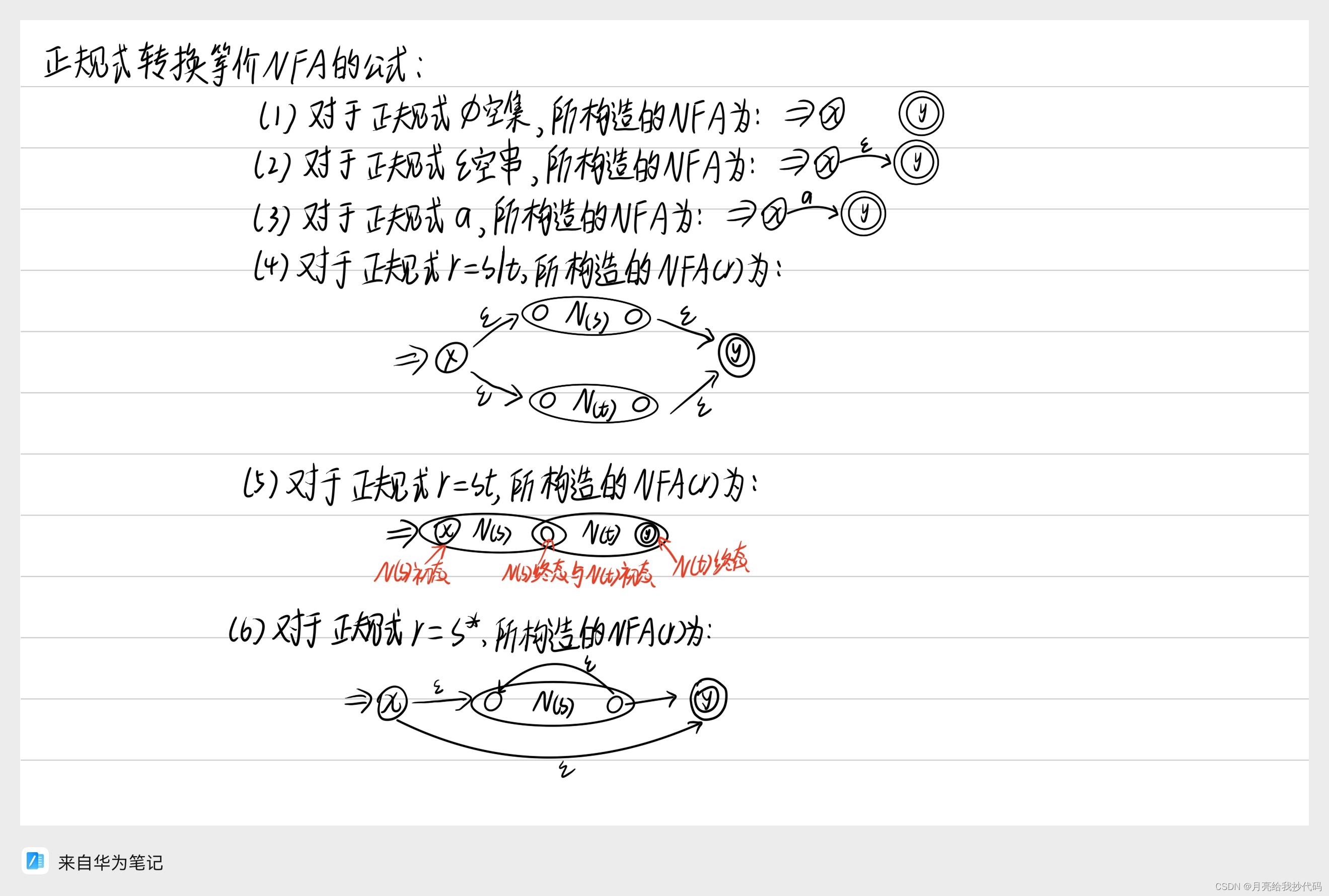
正规文法转换为 NFA
将正规文法转换为具有等价性的 NFA 十分简单,只需要根据正规文法产生式一步步描述出来即可,但是需要增加一个终态产生式。
假设当前存在正规文法 G[S]:S—>aA A—>b,转换为等价性的 NFA 过程如下所示:

转换示例:
将正规文法 G[S] 转换为具有等价性的 NFA。
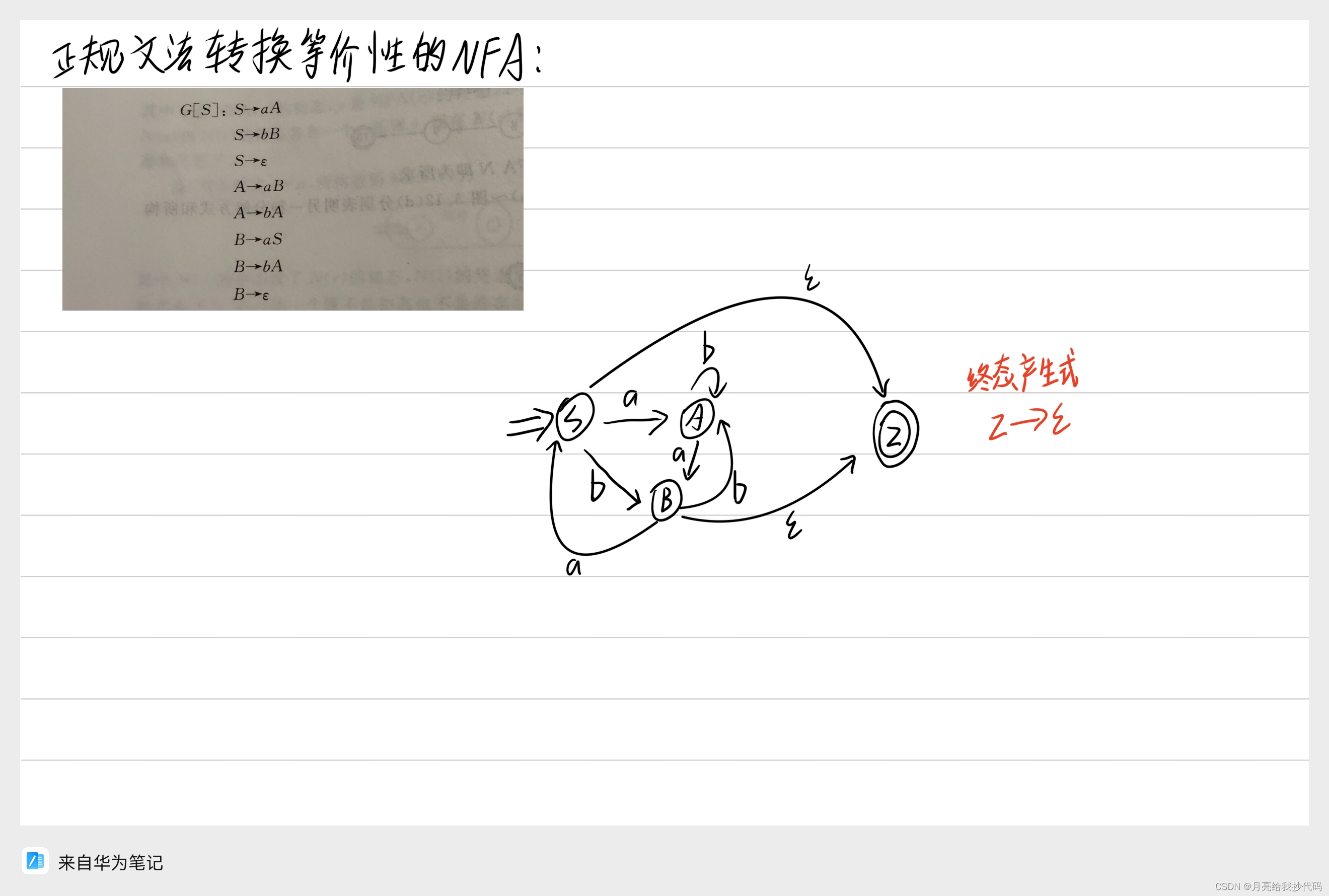
NFA 转换为正规文法
将 NFA 转换为正规文法同样简单,根据状态图直接可以的出结果,但是需要注意结果的格式书写。
正规文法结果由四部分组成,分别为:有穷集 K、有穷字母表 Σ、产生式 P 以及初态组成。
转换示例:
将下图所示的 NFA 转换为具有等价性的正规文法。

希望这篇文章对你有所帮助。