---

学习视频：《数值分析》| 华科 | 研究生基础课

---

一、引言

1.1 插值法引入

许多实际问题都用函数 $y=f(x)$ 来表示某种内在规律的数量关系，其中相当一部分函数是通过实验或计算得到的，并且只是 $[a,b]$ 上一系列点 $x_i$ 的函数值 { f ( x i )   ∣   i = 0 , 1 , . . . , n } \{f(x_i)\ |\ i=0,1,...,n\} {f(xi​) ∣ i=0,1,...,n}，这只是一张函数表。

有的问题虽然也有解析表达式，但由于计算复杂，使用不方便，通常也要构造一个函数表，如三角函数表、对数表、立方根表、平方根表等。

然而，为了研究函数的变化规律，往往需要知道不在函数表上的函数值，因此，我们希望根据给定的函数表做一个既可以反映函数 $f(x)$ 的特性，又便于计算的简单函数 $p(x)$，用 $p(x)$ 近似 $f(x)$。插值法就是根据函数表寻找简单函数 $p(x)$ 的方法之一。

寻找简单函数的问题又被称为函数逼近问题，下面给出了一个函数逼近问题的示例：

那么，什么样的函数是简单函数呢？

通常，我们用代数多项式或分段代数多项式作为简单函数 $p(x)$，并使得 $p(x_i)=f(x_i)$ 对所有的 $x_i,i=0,1,...,n$ 成立。

1.2 常用插值法

• 多项式插值：$p(x)$ 为多项式函数（最常用）
• 分段插值：$p(x)$ 为分段多项式函数
• 三角插值：$p(x)$ 为三角函数

1.3 插值法定义

二、插值法研究的问题

• 满足插值条件的 $p(x)$ 是否存在且唯一？
• 如满足插值条件的 $p(x)$ 存在，如何构造 $p(x)$？
• 如何估计用 $p(x)$ 近似替代 $f(x)$ 产生的误差？

2.1 插值多项式存在的唯一性

因此，通过上述的证明，可以得到如下定理：

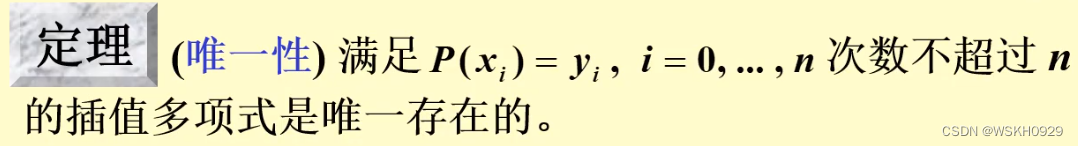
2.2 如何构造n次多项式

2.2.1 待定系数法

下面还有一种更加简洁的解法：

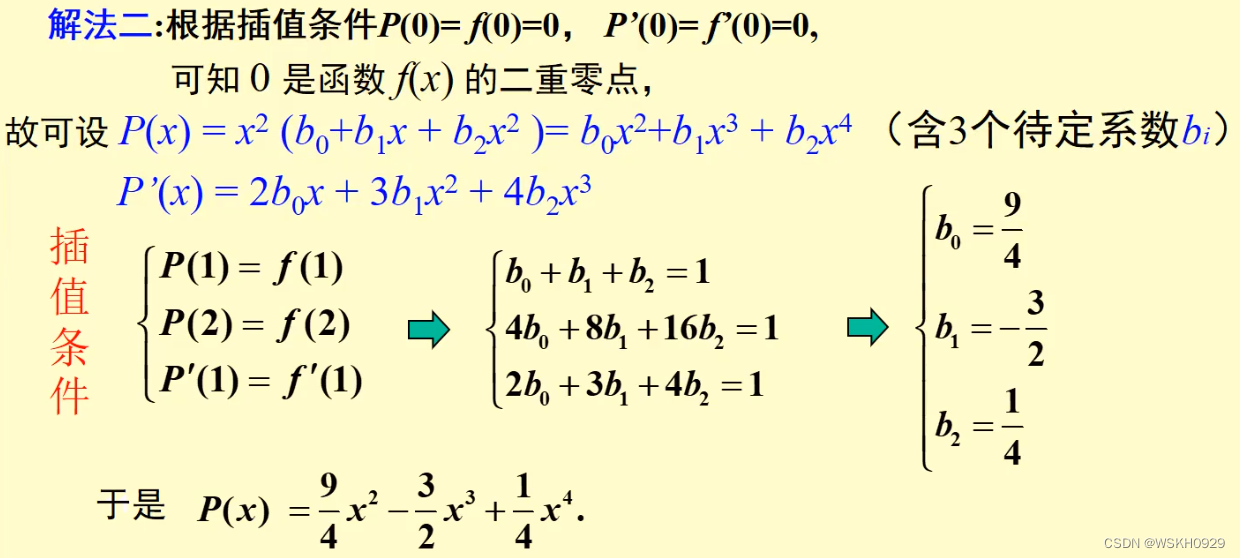
2.2.2 拉格朗日插值法

2.2.2.1 拉格朗日多项式

前面介绍的待定系数法中，使用的基函数是 $1,x,x^2,...,x^n$，这样的基函数过于简单，导致求解系数时较为麻烦。因此，有了下面将要介绍的拉格朗日插值法，它使用了更为复杂的拉格朗日基函数。

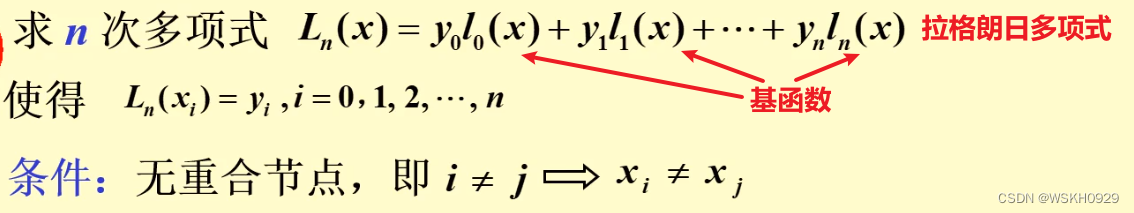
考虑 $n=1$ 的特殊情况：

由上可知：

$$\begin{gathered} l_0(x_0)=1,l_0(x_1)=0, \\ {l}_1(x_0)=0,l_1(x_1)=1. \end{gathered}$$

可以给出如下的克罗内克Delta函数：

$${\delta }_{ij}=\{\begin{array}{l}1,i=j\\ 0,i\ne j\end{array}$$

且满足条件 $l_i(x_j)={\delta }_{ij}$

更一般地，下面我们进一步讨论 $n\ge 1$ 的情况：

从拉格朗日基函数公式我们可以看出，它仅仅与节点 $x$ 有关，而与真实的函数形式 $f(x)$ 无关，这意味着给定不同的函数和相同的插值节点，求出来的拉格朗日基函数是一样的。

另外，容易得到 ${\sum }_i{l}_i(x)=1$（特别地，$f(x)=1$）

2.2.2.2 拉格朗日插值余项

假设节点 $x_i\in [a,b],i=0,1,...,n$，且 $f(x)$ 满足条件 $f(x)\in C^n[a,b]$，$f^{(n+1)}(x)$ 在 $[a,b]$ 内存在，考虑截断误差 $R_n(x)=L_n(x)-f(x)$

由插值条件可知，$R_n(x)$ 至少存在 $n+1$ 个零点（因为在每个插值点处，$R_n$ 必然为零），因此，可以将 $R_n(x)$ 表示为：

$$R_n(x)=K(x)\prod _{i=0}^n(x-x_i)$$

其中，$K(x)$ 是一个待确定的函数。

考虑任意一个非插值节点 $x\ne x_i(i=0,1,...,n)$，设辅助函数：
$$g(t)=R_n(t)-K(x)\prod _{i=0}^n(t-x_i)$$

容易得到，$g(t)$ 至少有 $n+2$ 个零点（$x$ 和 $x_0,x_1,...,x_n$）

根据罗尔定理的推广可得，在区间 $[a,b]$ 内至少存在一点 ${\xi }_x$ ，使得辅助函数的 $n+1$ 阶导函数为零，即 $g^{(n+1)}({\xi }_x)=0$，从而可以推导出：
$$R_n^{(n+1)}({\xi }_x)-K(x)(n+1)!=0$$

从而有：

$$f^{(n+1)}({\xi }_x)-L_n^{(n+1)}({\xi }_x)-K(x)(n+1)!=0$$

由于 $L_n$ 是 $n$ 次多项式，因此，$L_n^{(n+1)}({\xi }_x)=0$，所以有：

$$f^{(n+1)}({\xi }_x)-K(x)(n+1)!=0$$

从而推导出：$K(x)=\frac{f^{(n+1)}({\xi }_x)}{(n+1)!}$

将 $K(x)$ 代回得：

$$R_n(x)=\frac{f^{(n+1)}({\xi }_x)}{(n+1)!}\prod _{i=0}^n(x-x_i)$$

综上所述，我们可以得到如下的特殊情况：

另外，需要注意的是：

其中，第二点的意思是，如果原函数 $f(x)$ 的阶数等于 $n$，那么当使用 $m>n$ 个插值节点求出的拉格朗日插值多项式是精确的。

2.2.2.3 例题

例题1：

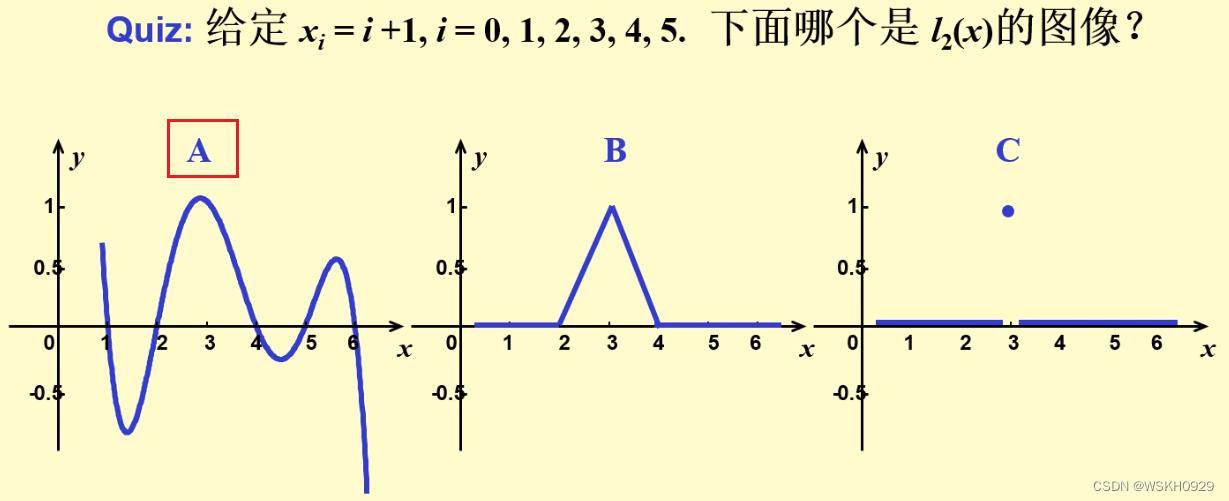
例题2：

从这个例题，可以发现，次数高的插值多项式误差更小。但绝对不是次数越高越好哦（次数过高会出现龙格现象）！

2.2.2.4 拉格朗日插值法的问题

拉格朗日插值法虽然简单易用，但是如果要增加或减少节点时，全部的基函数 $l_i(x)$ 都要重新计算，不太方便。

那么如何解决这个问题呢？

其实，上面的思想就是牛顿插值法的思想。本博客将在下面进行介绍。

2.2.3 牛顿插值法

2.2.3.1 牛顿插值思想

2.2.3.2 差商的定义

在介绍牛顿插值公式之前，我们需要介绍**差商（均差）**的定义：

首先给出一阶差商的定义式：

然后基于一阶差商，给出二阶差商的定义式（其实就是一阶差商的一阶差商）：

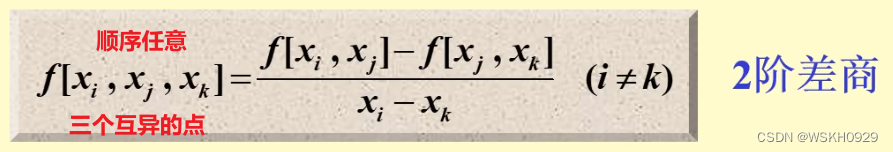
最后，写出 $k+1$ 阶差商的定义式：

需要注意的是，$k$ 阶差商必须由 $k+1$ 个节点构成， $k$ 个节点是构造不出 $k$ 阶差商的。

为了统一起见，补充定义函数 $f(x_0)$ 为零阶差商，差商的值与 $x_i$ 的顺序无关。

2.2.3.3 差商的性质

定义 $\omega$ 如下：

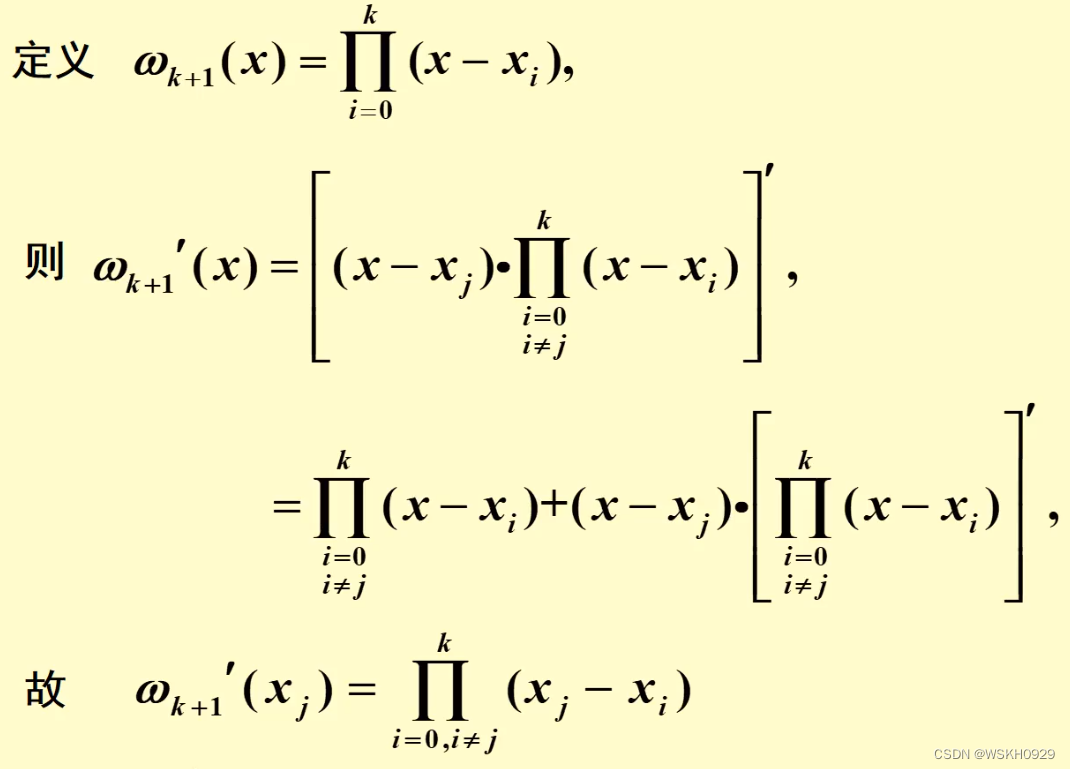
然后，可以给出差商的4点性质：

2.2.3.4 差商表

差商表方便在编程的时候计算不同阶数的差商。

有了差商表，我们可以很容易通过递推的方式计算差商：

2.2.3.5 牛顿插值公式

牛顿插值是通过选取特殊的基函数来实现的，这时，取

$$\begin{gathered} {\phi }_0(x)=1 \\ {\phi }_{i+1}(x)=(x-x_i){\phi }_i(x)i=0,1,...,n-1 \end{gathered}$$

作为牛顿插值的以 $x_0,x_1,...,x_n$ 为节点的基函数，而次数不超过 $n$ 的多项式 $N_n(x)$ 可表示为：

$$N_n(x)=c_0+c_1(x-x_0)+c_2(x-x_0)(x-x_1)+...+c_n(x-x_0)(x-x_1)...(x-x_{n-1})$$

其中，$c_0,c_1,...,c_n$ 是待定系数，由插值条件决定。

带入插值条件很容易计算得：

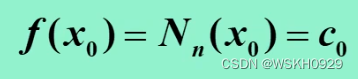
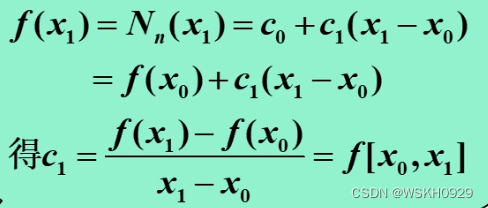
根据上述结果，运用数学归纳法可以求得：

$$c_k=f[x_0,x_1,...,x_k]$$

因此就得到下面的满足插值条件的 $n$ 次牛顿插值多项式：

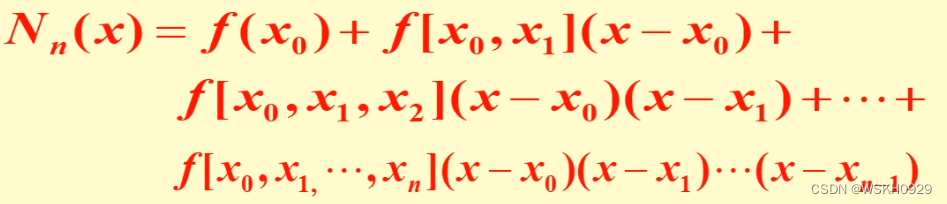
2.2.3.6 牛顿插值余项

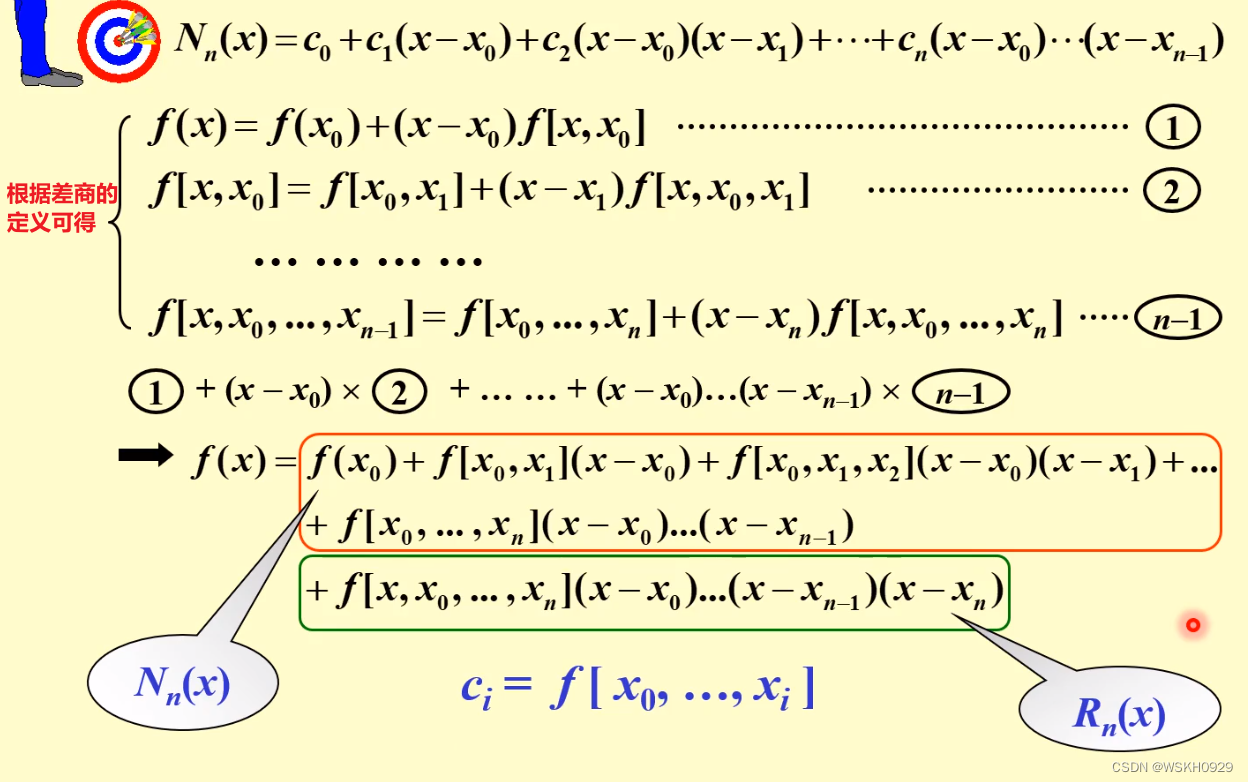
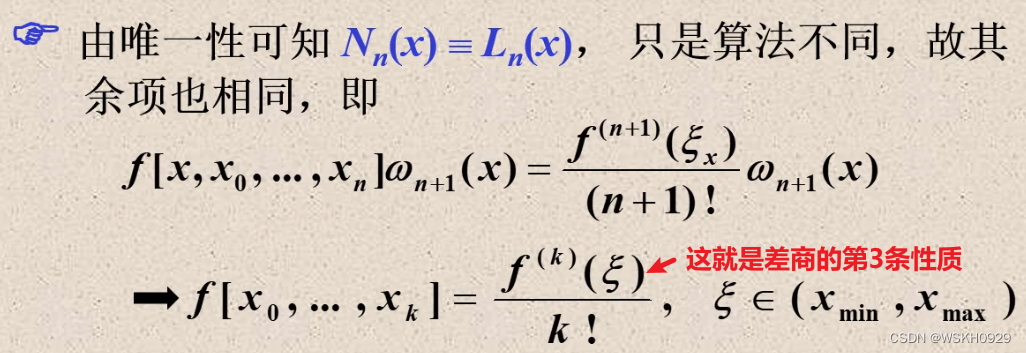
2.2.3.7 等距节点公式

当节点等距分布时：$x_i=x_0+ih(i=0,1,...,n)$，利用差分，减少差商的除法运算次数，提高效率，下面是关于差分的定义

然后是一些关于差分的性质：

然后介绍前插和后插公式：

当 $x$ 靠近 $x_0$ 时用前插公式，否则用后插公式

使用牛顿前插或者后插公式，先构造差分表如下：

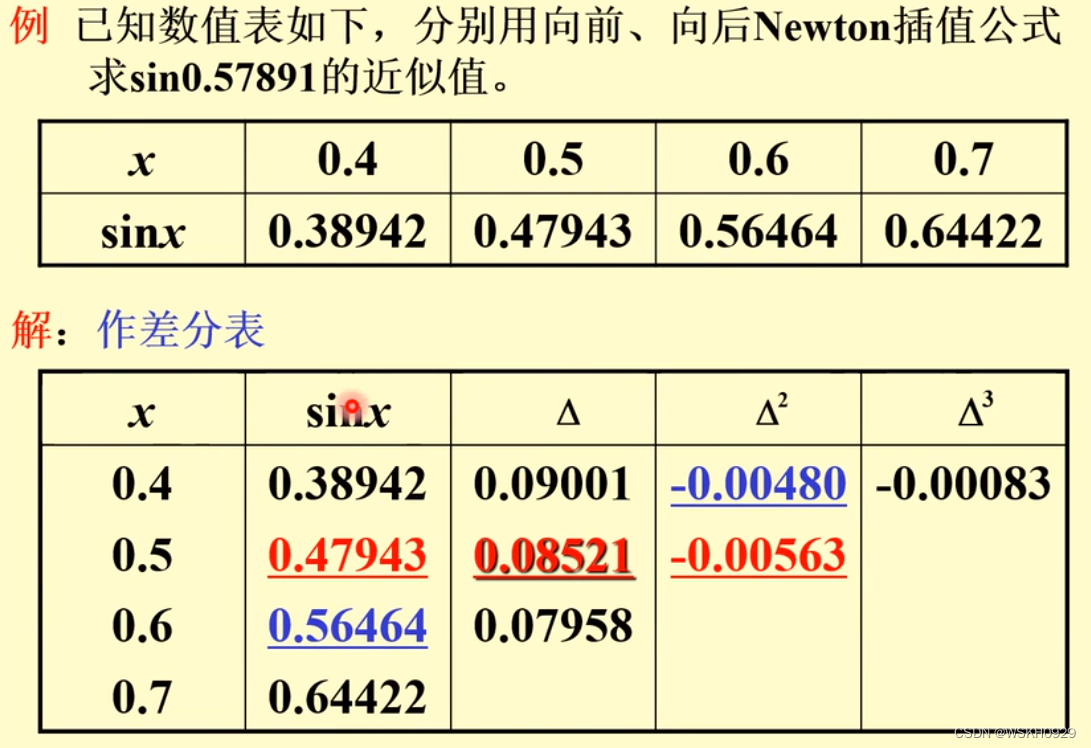
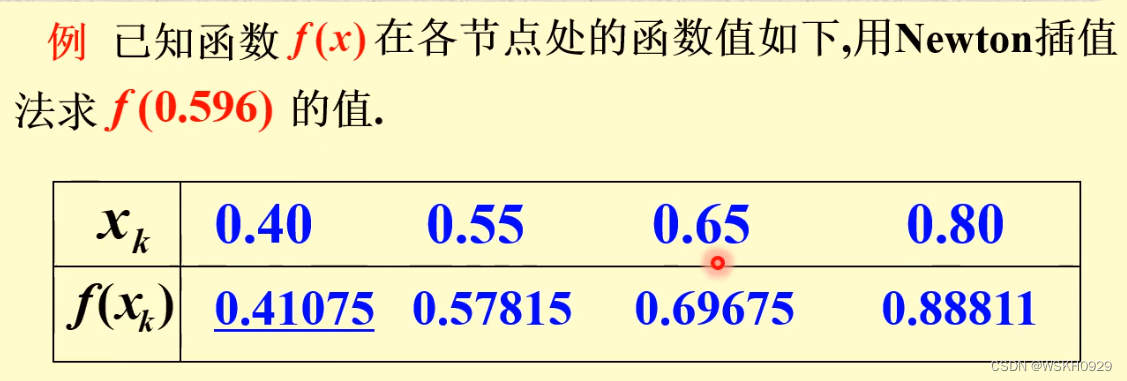
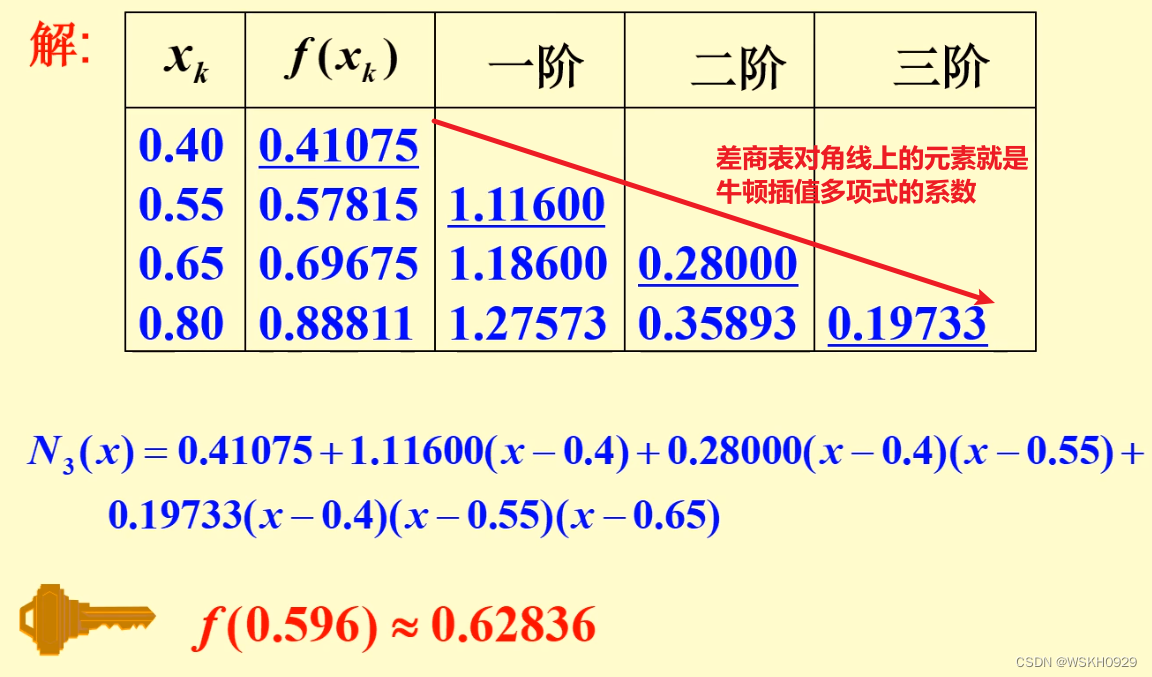
2.2.3.8 例题

例题1：

例题2：