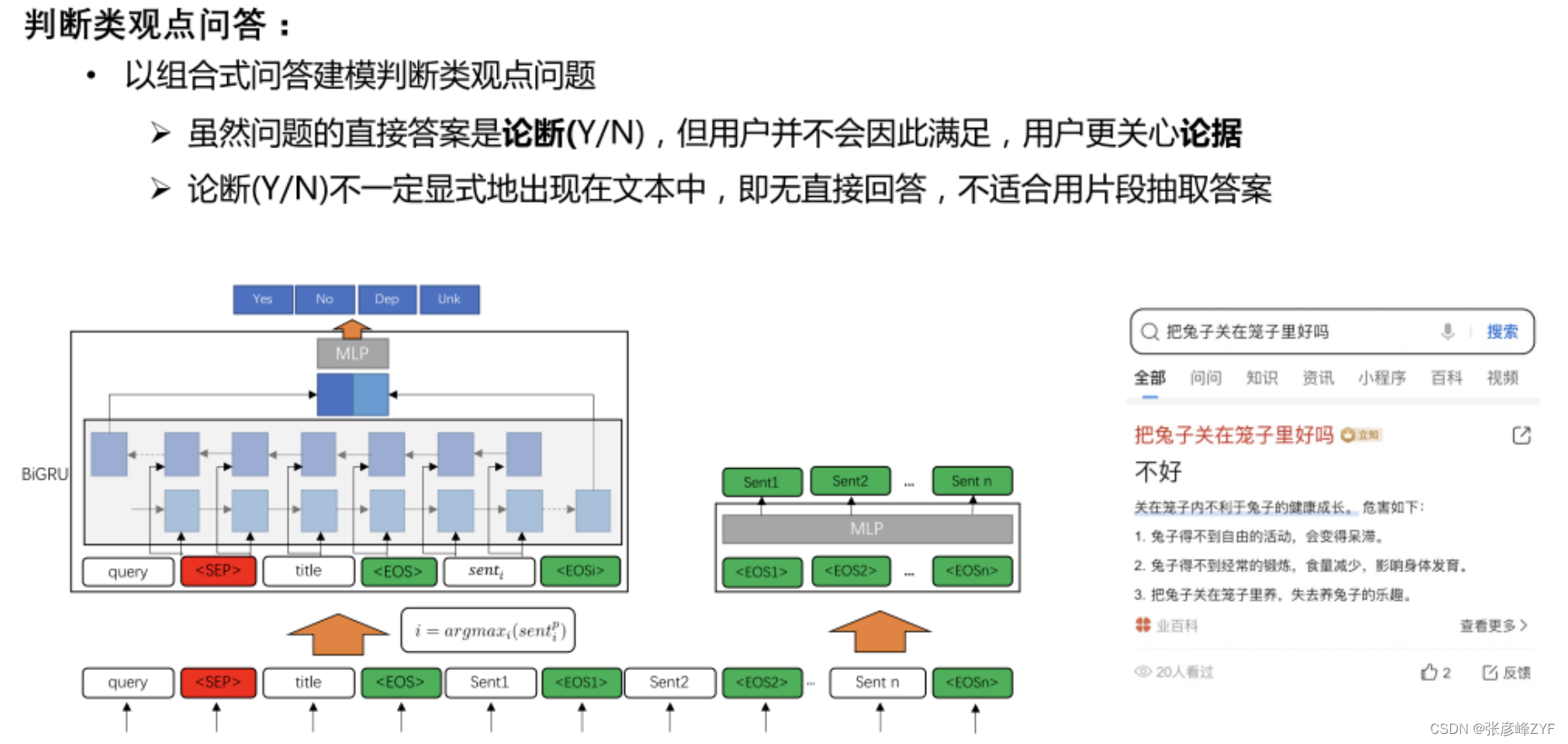
为了同学们能理好的理解数在计算机内的表示,我们可以把计算机中的整数看成N位进制数的数轮,N一般为2的幂,如下:
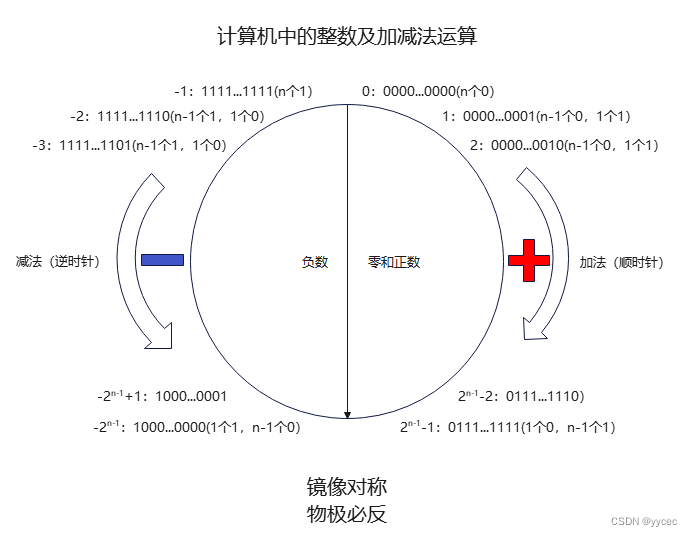
我们来举个例子:如果用4位二进制来表示整数,则可以表示的整数范围为-8(即)到+7(即
),如下表所示(上下对称):
| 非负数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | |
| 负数 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 |
| 1111 | 1110 | 1101 | 1100 | 1011 | 1010 | 1001 | 1000 |
物极必反之加法:-1再加1变为0(1111+1=10000,高位溢出,结果为0); +7再加1变为-8 (0111+1=1000)
物极必反之减法:相反 0 - 1 变成-1 (0000-0001,不够减向高位借,即1000-0001=1111)
-8 减 1 变成 +7:1000-0001 = 0111(+7)
注意:计算机中是没有减法的,减去一个数是通过加上这个负数原码的补码来实现的(即以上),减法是加法的补运算(电路也这样实现的,后面的计算机系统基础课程中要讲)
通过上面的二进制数轮,相信大家能看出计算机运算的基本原理了,在编程程序时要学会使用适当的数据类型来处理数据。