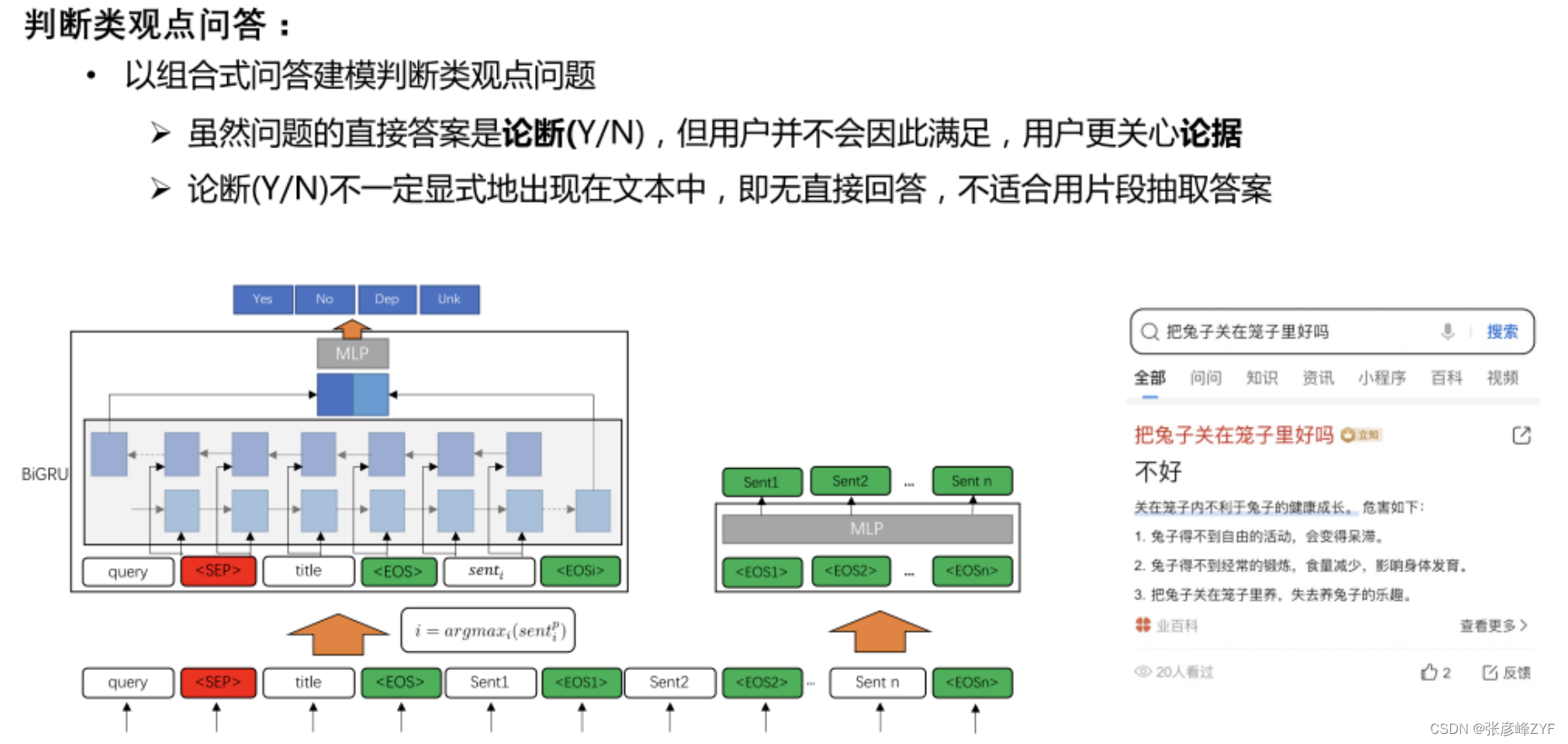
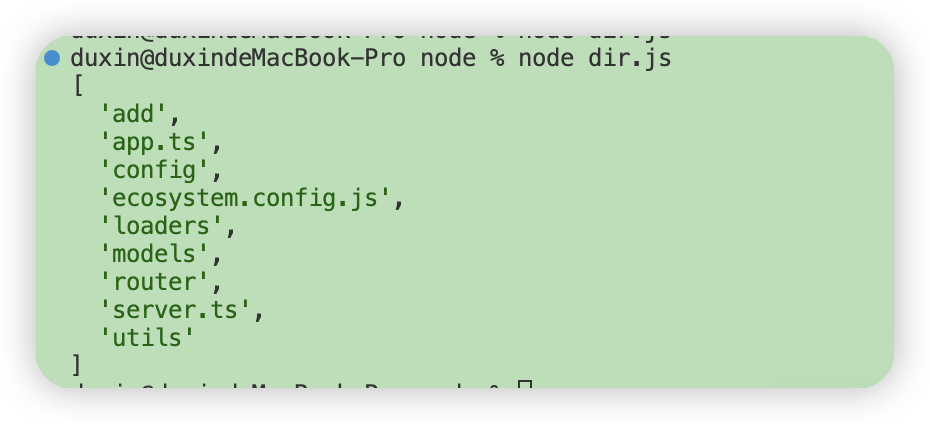
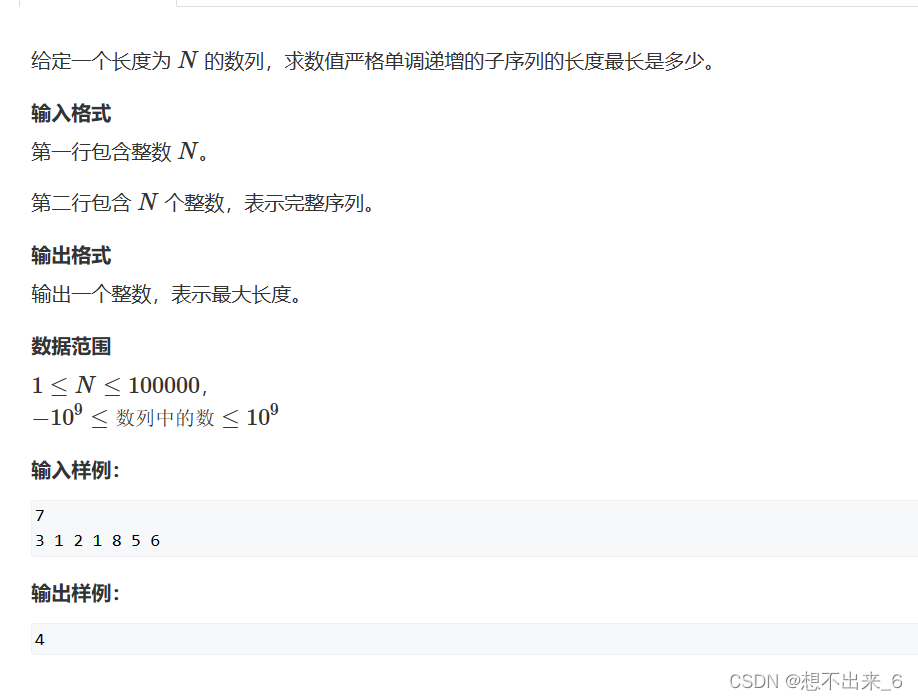
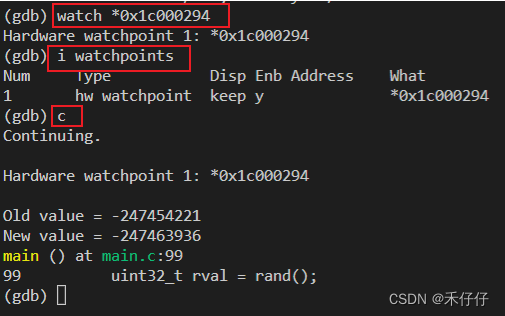
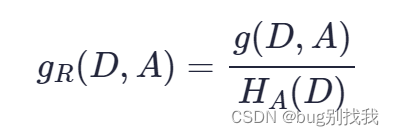详细介绍如何使用Ipopt非线性求解器求解带约束的最优化问题

news2024/11/15 8:10:11

   本文中将详细介绍如何使用Ipopt非线性求解器求解带约束的最优化问题，结合给出的带约束的最优化问题示例，给出相应的完整的C++程序，并给出详细的解释和注释，以及编译规则等

   一、Ipopt库的安装和测试

   本部分内容在之前的文章《Ubuntu20.04安装Ipopt的流程介绍及报错解决方法（亲测简单有效）》中已经详细介绍过了，链接如下：

   https://blog.csdn.net/qq_44339029/article/details/133679131

   二、使用Ipopt非线性求解器求解带约束的最优化问题的程序示例

   0、明确要求解的带约束的最优化问题

   首先，我们来看一个简单的带约束的最优化问题，其包含两个不等式约束和1个等式约束，详情如下：

   f = ( x 1 − 10.24 ) 2 + 5.21 x 2 + 9.9 ( x 3 − x 4 ) 2 f=(x_1-10.24)^2+5.21x_2+9.9(x_3-x_4)^2 f=(x1​−10.24)2+5.21x2​+9.9(x3​−x4​)2

   g 1 : 2 ≤ x 3 − x 4 ≤ 10 g 2 : 2.99 ≤ x 2 ≤ 100 g 3 : x 2 = x 4 \begin{aligned}g_1 & : & 2\leq x_3-x_4\leq10\\ g_2 & : & 2.99\leq x_2\leq100\\ g_3 & : & x_2=x_4\end{aligned} g1​g2​g3​​:::​2≤x3​−x4​≤102.99≤x2​≤100x2​=x4​​

   其中 x 1 x_1 x1​、 x 2 x_2 x2​、 x 3 x_3 x3​、 x 4 x_4 x4​的取值范围均为0~100，易知使得上述目标函数 f f f取值最小的解为：10.24、2.99、4.99、2.99。

   下面介绍，如何编程使用Ipopt非线性求解器求解该问题

   1. 引入头文件和命名空间：

#include <iostream>
#include <cassert>
#include <cppad/ipopt/solve.hpp>
using CppAD::AD;

   引入必要的C++头文件，包括iostream（用于输入输出），cassert（用于C风格的assert）以及cppad/ipopt/solve.hpp（用于Ipopt求解器和CppAD库的接口）。然后在一个匿名的命名空间中引入了AD类型，这是CppAD库中用于自动微分（Automatic Differentiation）的数据类型。

   2. 定义FG_eval类：

namespace {
    class FG_eval {
    public:
        typedef CPPAD_TESTVECTOR(AD<double>) ADvector;
        
        void operator()(ADvector& fg, const ADvector& x) {
            // ...
        }
    };
}

   在匿名命名空间中，定义一个FG_eval类，用于计算目标函数和约束条件的值。这个类也是调用使用CppAD和Ipopt库所需的最重要的接口，这个类中的operator()函数是用于计算问题的目标函数和约束条件的核心部分。它接受两个向量：fg用于存储目标函数值和约束条件值，x用于存储优化变量。

   3. 定义operator()函数：

   接下来，我们根据第0步中明确的目标函数及约束条件来编写核心的operator函数，示例如下：

void FG_eval::operator()(ADvector& fg, const ADvector& x) {
    assert(fg.size() == 4);
    assert(x.size() == 4);

    AD<double> x1 = x[0];
    AD<double> x2 = x[1];
    AD<double> x3 = x[2];
    AD<double> x4 = x[3];

    fg[0] = (x1 - 10.24) * (x1 - 10.24) + 5.21 * x2 + 9.9 * (x3 - x4) * (x3 - x4);
    fg[1] = x3 - x4;
    fg[2] = x2;
    fg[3] = x2 - x4;
    
    // 打印计算结果
    std::cout << "fg[0]:" << fg[0] << std::endl;
    std::cout << "fg[1]:" << fg[1] << std::endl;
    std::cout << "fg[2]:" << fg[2] << std::endl;
    std::cout << "fg[3]:" << fg[3] << std::endl;
}

   operator()函数接受fg和x向量，然后根据问题的定义计算目标函数和约束条件的值，并将它们存储在fg向量中。同时，它也打印出这些值， 其中fg[0]即为目标函数表达式、fg[1]、fg[2]、fg[3]中依次对应了第0步中设定的三个约束，不等式约束直接写即可，等式约束的等式左右两边同时减去右边的项，使等式右边变为0。

   4. 定义主函数get_started（该函数名字可任取）：

   定义一个主函数，设定自变量的初始值，以及自变量和约束的上下限，设定和提供调用Ipopt非线性求解器求解所需要的变量，然后调用求解器进行求解，并进行验证等操作，程序示例如下：

bool get_started(void)
{	bool ok = true;
	size_t i;
	typedef CPPAD_TESTVECTOR( double ) Dvector;
	size_t nx = 4;
	size_t ng = 3;
	Dvector xi(nx);
	xi[0] = 10.0;
	xi[1] = 5.0;
	xi[2] = 5.0;
	xi[3] = 100.0;
	Dvector xl(nx), xu(nx);
	for(i = 0; i < nx; i++)
	{	xl[i] = 0;
		xu[i] = 100;
	}

	Dvector gl(ng), gu(ng);
	gl[0] = 2;     gu[0] = 10;
	gl[1] = 2.99;  gu[1] = 100;
	gl[2] = 0;     gu[2] = 0;

	FG_eval fg_eval;
	std::string options;
	options += "Integer print_level  0\n";
	options += "String  sb           yes\n";
	options += "Integer max_iter     10\n";
	options += "Numeric tol          1e-6\n";
	options += "String  derivative_test            second-order\n";
	options += "Numeric point_perturbation_radius  0.\n";
	CppAD::ipopt::solve_result<Dvector> solution;
	CppAD::ipopt::solve<Dvector, FG_eval>(
		options, xi, xl, xu, gl, gu, fg_eval, solution
	);
	
	ok &= solution.status == CppAD::ipopt::solve_result<Dvector>::success;
	double check_x[]  = { 10.24, 2.99, 4.99, 2.99 }; 
	double rel_tol    = 1e-6;  // relative tolerance
	double abs_tol    = 1e-6;  // absolute tolerance
	for(i = 0; i < nx; i++)
	{		
		ok &= CppAD::NearEqual(
			check_x[i],  solution.x[i],   rel_tol, abs_tol     
		); 
        std::cout << "x[" << i << "] = " << solution.x[i] << std::endl;
	}
	return ok;
}

   以下是程序的详细解释：

   （1）. bool get_started(void)：程序逻辑流程的主要函数，get_started函数定义了问题的基本参数，如变量数量、约束数量、变量的初始值，以及变量和约束的上下界。然后，它创建了一个FG_eval对象来计算目标函数和约束条件，设置了Ipopt求解器的选项，并最终调用求解器来解决问题。

   （2）. bool ok = true;：定义一个布尔变量 ok，用于表示问题是否成功求解。一开始将其初始化为 true。

   （3）. 类型别名 Dvector：通过 typedef CPPAD_TESTVECTOR(double) Dvector; 定义了一个 Dvector 类型，它是CppAD库中的向量类型，用于存储双精度（double）数值。

   （4）. size_t nx = 4;：定义一个 size_t 类型的变量 nx，表示问题中独立变量（自变量）的数量，即问题的变量维度。在这个示例中，有4个独立的自变量。

   （5）. size_t ng = 3;：定义一个 size_t 类型的变量 ng，表示问题中的约束数量，即约束的维度。在这个示例中，有3个约束条件。

   （6）. 创建 Dvector 向量 xi：用于存储问题的独立变量（自变量）。这个向量有4个元素，对应于4个自变量。

   （7）. 设置初始猜测值 xi：为 xi 向量中的每个元素分别赋初值，为检验算法性能，这里设定了一个较差的初始值。

   - `xi[0] = 10.0;`
   - `xi[1] = 5.0;`
   - `xi[2] = 5.0;`
   - `xi[3] = 100.0;`

   （8）. 定义变量和约束条件的上下界：

   - 创建 Dvector 向量 xl 和 xu，它们分别表示变量的下界和上界，并根据第0步中的设定的自变量的取值范围0~100进行设定

   - 创建 Dvector 向量 gl 和 gu，它们分别表示约束条件的下界和上界，并根据第0步中，三个约束的进行设定，对于前两个不等式约束，直接设定即可，第三个等式约束，即 x 2 − x 4 = 0 x_2-x_4=0 x2​−x4​=0,因此，上下限均设为0即可。

   （9）. 创建 FG_eval 类的对象 fg_eval：FG_eval 即我们第二步中设定的类，用于计算目标函数和约束条件的值。这是问题的目标函数和约束条件的具体定义。

   （10）. 创建字符串 options：用于存储Ipopt求解器的选项，包括设置输出级别、最大迭代次数、收敛容差等，详情如下所示：

    - `options += "Integer print_level  0\n";`：将输出级别设置为0，以关闭求解器的详细输出，只打印关键信息。
    - `options += "String  sb           yes\n";`：使用平衡约束优化方法。
    - `options += "Integer max_iter     10\n";`：设置最大迭代次数为10次。
    - `options += "Numeric tol          1e-6\n";`：设置迭代停止的收敛容差为1e-6。
    - `options += "String  derivative_test            second-order\n";`：启用二阶导数测试，用于检查目标函数和约束条件的导数是否正确。
    - `options += "Numeric point_perturbation_radius  0.\n";`：将随机扰动的半径设置为0，表示不使用扰动进行数值近似求导。

   （11）. 创建 CppAD::ipopt::solve_result<Dvector> solution;：用于存储求解结果的对象。

   （12）. 调用 CppAD::ipopt::solve 函数：使用Ipopt求解器解决非线性规划问题。传递了问题选项、独立变量的初始值、变量的上下界、约束条件的上下界、问题的定义（fg_eval 对象），以及存储结果的 solution 对象。

   （13）. 检查求解器的状态：如果状态为成功（success），则将 ok 变量保持为真，表示问题已成功求解。

   注：下面的第(14)~(16)部分，是为了验证求解是否正确，为非必要步骤

   （14） 创建 check_x 数组：包含问题的精确解。这些值是问题的已知精确解。

   （15）. 设置相对容差和绝对容差的阈值：这些值用于控制验证解的精度。

   （16）. 遍历问题中的每个变量，进行解的验证：使用 CppAD::NearEqual 函数来比较问题的解与精确解是否足够接近。如果它们的差距在相对容差和绝对容差的范围内，ok 变量将保持为真，并打印每个变量的解。

   （17）.返回 ok 变量：表示问题是否成功求解。

  

   5. C++主函数main：

int main(void) {
    std::cout << "===== Ipopt with CppAD Testing =====" << std::endl;
    bool result = get_started();
    std::cout << "Final checking: " << result << std::endl;
}

   main函数是程序的入口点，它简单地调用get_started函数来执行非线性规划问题的求解，并打印结果。

   6. ☆☆☆带详细注释的完整程序`☆☆☆

# include <iostream>
// C style asserts
# include <cassert>
// 包含Ipopt求解器头文件
# include <cppad/ipopt/solve.hpp>


// 在一个匿名的命名空间中，引入了一个AD类型，它是CppAD库中用于自动微分（Automatic Differentiation）的数据类型。AD类型可以用来表示变量和函数，使其具备微分能力。
namespace {
	using CppAD::AD;

	class FG_eval {
	public:
		typedef CPPAD_TESTVECTOR( AD<double> ) ADvector;
        // fg: function that evaluates the objective and constraints using the syntax
		// 定义一个函数运算符，用于计算目标函数和约束条件的值
		void operator()(ADvector& fg, const ADvector& x)
		{	
			//使用assert来设定fg和x的大小，以确保它们与问题的维度匹配
			//fg 向量用于存储目标函数值和约束条件值，x向量用于存储优化变量
			assert( fg.size() == 4 );
			assert( x.size()  == 4 );

			//  将 x 中的优化变量分配给 AD 类型的变量 x1 到 x4。这是在使用C++ Algorithmic Differentiation（CppAD）时定义问题中的独立变量的方式。
			AD<double> x1 = x[0];
			AD<double> x2 = x[1];
			AD<double> x3 = x[2];
			AD<double> x4 = x[3];
			// 计算目标函数的值，将其存储在 fg[0] 中。这里使用了 x1 到 x4 这些 AD 类型的变量，这意味着这个表达式将被自动微分，以便后续的梯度计算。
			fg[0] = (x1-10.24) * (x1-10.24) + 5.21*x2 + 9.9*(x3-x4)*(x3-x4);
			//  分别计算三个约束条件的值，并将它们存储在 fg[1] 和 fg[2]、 fg[3]中。
			fg[1] = x3-x4;
			fg[2] = x2;
            fg[3] = x2-x4;
			//
			std::cout << "fg[0]:" << fg[0]<< std::endl;
			std::cout << "fg[1]:" << fg[1]<< std::endl;
			std::cout << "fg[2]:" << fg[2]<< std::endl;
            std::cout << "fg[3]:" << fg[3]<< std::endl;

			return;
		}
	};
}

// 该函数用于设置和解决非线性规划问题
// 它首先定义了问题的一些基本参数，如变量数量、约束数量、变量的初始值、变量和约束的上下界等
// 然后创建一个FG_eval对象用于计算目标函数和约束条件
// 最后，使用CppAD::ipopt::solve函数来解决问题，并将结果存储在solution中
bool get_started(void)
{	bool ok = true;
	size_t i;
	// 创建了一个类型别名 Dvector，它是CppAD库中的一个向量类型，用于存储双精度（double）数值。这个向量类型是CppAD库的一部分，通常用于存储问题的变量、约束和其他向量。
	typedef CPPAD_TESTVECTOR( double ) Dvector;

	// 声明了一个 size_t 类型的变量 nx，它表示问题中独立变量（自变量）的数量，也就是问题的变量维度。在这个示例中，有4个独立变量，因此 nx 的值为4。
	size_t nx = 4;
	// 声明了一个 size_t 类型的变量 ng，它表示问题中的约束数量，也就是约束的维度。在这个示例中，有3个约束条件，因此 ng 的值为3。
	size_t ng = 3;
	//  创建了一个名为 xi 的 Dvector 类型的向量，用于存储问题的独立变量（自变量）。这个向量有4个元素，对应于4个自变量。
	Dvector xi(nx);
	// 分别为这4个独立变量设置了初始值。这些值将用作问题的初始猜测，作为非线性规划求解器的起点。
	xi[0] = 10.0;
	xi[1] = 5.0;
	xi[2] = 5.0;
	xi[3] = 100.0;

	//设置问题的变量（自变量）和约束条件的上下界（限制条件）。
	Dvector xl(nx), xu(nx);
	for(i = 0; i < nx; i++)
	{	xl[i] = 0;
		xu[i] = 100;
	}

	Dvector gl(ng), gu(ng);
	gl[0] = 2;     gu[0] = 10;
	gl[1] = 2.99;  gu[1] = 100;
	gl[2] = 0;     gu[2] = 0;

	// 创建了 FG_eval 类的对象 fg_eval，用于计算目标函数和约束条件的值。这是问题的目标函数和约束条件的具体定义。
	FG_eval fg_eval;

	// 创建了一个字符串 options，用于存储Ipopt求解器的选项。
	std::string options;
	// 设置了求解器选项，将 print_level 参数设置为0，以关闭求解器的输出，即不会在控制台打印详细信息，只打印关键信息。
	options += "Integer print_level  0\n";
	//  将 sb 参数设置为 "yes"，这表示使用平衡约束优化方法。
	options += "String  sb           yes\n";
	// 设置最大迭代次数为10次。
	options += "Integer max_iter     10\n";
	// approximate accuracy in first order necessary conditions;
	// see Mathematical Programming, Volume 106, Number 1,
	// Pages 25-57, Equation (6)
	// 设置迭代停止的收敛容差为1e-6。
	options += "Numeric tol          1e-6\n";
	//  启用了二阶导数测试，用于检查目标函数和约束条件的导数是否正确。
	options += "String  derivative_test            second-order\n";
	// maximum amount of random pertubation; e.g.,
	// when evaluation finite diff
	// 将随机扰动的半径设置为0，表示不使用扰动进行数值近似求导。
	options += "Numeric point_perturbation_radius  0.\n";

	// 创建了一个用于存储求解结果的对象 solution，
	CppAD::ipopt::solve_result<Dvector> solution;

	// 调用了 CppAD::ipopt::solve 函数，用于解决非线性规划问题。它传递了问题选项、独立变量的初始值、变量的上下界、约束条件的上下界、问题的定义（fg_eval 对象），以及存储结果的 solution 对象。
	CppAD::ipopt::solve<Dvector, FG_eval>(
		options, xi, xl, xu, gl, gu, fg_eval, solution
	);

	//检查求解器的状态，如果状态为成功（success），则 ok 变量将保持为真。这表示问题已成功求解。
	ok &= solution.status == CppAD::ipopt::solve_result<Dvector>::success;
	// 创建一个名为 check_x 的数组，其中包含了问题的精确解。这个数组中的值是问题的已知精确解。
	double check_x[]  = { 10.24, 2.99, 4.99, 2.99 }; 
	// 设置了相对容差和绝对容差的阈值。这些值用于控制验证解的精度。
	double rel_tol    = 1e-6;  // relative tolerance
	double abs_tol    = 1e-6;  // absolute tolerance
	// 遍历问题中的每个变量，进行解的验证。
	for(i = 0; i < nx; i++)
	{	
		//使用 CppAD::NearEqual 函数来比较问题的解 solution.x[i] 与精确解 check_x[i] 是否足够接近。如果它们的差距在相对容差和绝对容差的范围内，ok 变量将保持为真。
		ok &= CppAD::NearEqual(
			check_x[i],  solution.x[i],   rel_tol, abs_tol     
		); 
		// 使用 std::cout 打印每个变量的解，以便在控制台上查看结果。
        std::cout << "x[" << i << "] = " << solution.x[i] << std::endl;
	}

	return ok;
}

// main program that runs all the tests
int main(void)
{	
    std::cout << "===== Ipopt with CppAD Testing =====" << std::endl;
    bool result = get_started();
    std::cout << "Final checking: " << result << std::endl;
}
// END C++

   三、编译验证

   将上面第二部分，第6步中给出的完整的程序，保存为CppAD_Ipopt.cpp，然后在同一目录下，创建一个名为CMakeLists.txt的文件，接下来，我们需要在CMakeLists.txt文件中，编写编译规则，如下所示：

# 设置CMake的最低版本要求
cmake_minimum_required(VERSION 3.5)
# 项目名称
project(CppadIpoptDemo)
# 寻找Ipopt包（确保你已经安装了Ipopt和CppAD）
# find_package(Ipopt REQUIRED)
# 设置可执行文件的名称和源文件
add_executable(cppad_ipopt_demo CppAD_Ipopt.cpp)
# 包含Ipopt的头文件
# target_include_directories(cppad_ipopt_demo PRIVATE ${IPOPT_INCLUDE_DIRS})
# 链接Ipopt库
# target_link_libraries(cppad_ipopt_demo ${IPOPT_LIBRARIES})
TARGET_LINK_LIBRARIES(cppad_ipopt_demo ipopt)

   保存，并关掉CMakeLists.txt文件，接下来就利用该文件对CppAD_Ipopt.cpp进行编译，在该目录下空白处，右键打开终端，依次输入以下四条语句

mkdir build

cd build

cmake ..

make

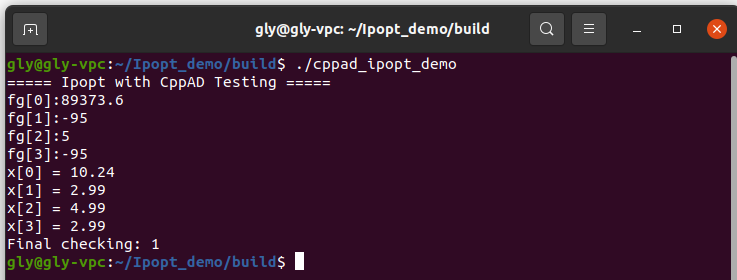
   以上编译结束后，在build文件夹下，生成了可执行文件cppad_ipopt_demo，如下图所示

   在当前目录下，右键打开终端，输入以下指令运行该文件

./cppad_ipopt_demo

   运行结果如下，可以发现即使在给定的初始解很差的情况下，Ipopt非线性求解器依然能够求解出第二部分第0部步中设定的带约束优化问题的最优解。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1122201.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

STM32-LTC6804方案成熟BMS方案

STM32-LTC6804方案成熟BMS方案

方案下载链接&#xff01;&#xff01;https://mp.weixin.qq.com/s?__bizMzU2OTc4ODA4OA&mid2247549092&idx1&snc73855c4e3d5afddd8608d8528864f95&chksmfcfb1373cb8c9a65a4bd1f545a1a587af882f209e7ccbb8944f4d2514d241ca1d7fcc4615e10&token539106225&a…
阅读更多...
【字符函数】

【字符函数】

✨博客主页&#xff1a;小钱编程成长记 &#x1f388;博客专栏&#xff1a;进阶C语言 &#x1f388;相关博文&#xff1a;字符串函数&#xff08;一&#xff09;、字符串函数&#xff08;二&#xff09; 字符函数 字符函数1.字符分类函数1.1 iscntrl - 判断是否是控制字符1.2 i…
阅读更多...
【GWO-KELM预测】基于灰狼算法优化核极限学习机回归预测研究（matlab代码实现）

【GWO-KELM预测】基于灰狼算法优化核极限学习机回归预测研究（matlab代码实现）

&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️&#x1f4a5;&#x1f4a5; &#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑清晰&#xff0c;为了方便读者。 ⛳️座右铭&a…
阅读更多...
【Java基础面试四十六】、 List＜? super T＞和List＜? extends T＞有什么区别？

【Java基础面试四十六】、 List＜? super T＞和List＜? extends T＞有什么区别？

文章底部有个人公众号&#xff1a;热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享&#xff1f; 踩过的坑没必要让别人在再踩&#xff0c;自己复盘也能加深记忆。利己利人、所谓双赢。 面试官&#xff1a;问题 参考答案&#x…
阅读更多...
蓝桥每日一题(day 4: 蓝桥592.门牌制作)--模拟--easy

蓝桥每日一题(day 4: 蓝桥592.门牌制作)--模拟--easy

#include <iostream> using namespace std; int main() {int res 0;for(int i 1; i < 2021; i ){int b i;while(b){if (b % 10 2) res ;b / 10;}}cout << res; return 0; }
阅读更多...
FFmpeg和rtsp服务器搭建视频直播流服务

FFmpeg和rtsp服务器搭建视频直播流服务

下面使用的是ubuntu的&#xff0c;window系统可以参考&#xff1a; 通过rtsp-simple-server和ffmpeg实现录屏并发布视频直播_rtsp simple server_病毒宇宇的博客-CSDN博客 一、安装rtsp-simple-server &#xff08;1&#xff09;下载rtsp-simple-server 下载地址&#xff1a;R…
阅读更多...
搜索问答技术学习：基于知识图谱+基于搜索和机器阅读理解（MRC）

搜索问答技术学习：基于知识图谱+基于搜索和机器阅读理解（MRC）

目录 一、问答系统应用分析 二、搜索问答技术与系统 &#xff08;一&#xff09;需求和信息分析 问答需求类型 多样的数据源 文本组织形态 &#xff08;二&#xff09;主要问答技术介绍 发展和成熟度分析 重点问答技术基础&#xff1a;KBQA和DeepQA KBQA&#xff08;…
阅读更多...
Python高级技巧

Python高级技巧

十三、Python高级技巧 1. 闭包 解决全局变量问题&#xff1a; 代码在命名空间上&#xff08;变量定义&#xff09;不够干净、整洁全局变量又被修改的风险 定义&#xff1a; ​ 在函数嵌套的前提下&#xff0c;内部函数使用了外部函数的变量&#xff0c;并且外部函数返回了内部…
阅读更多...
什么是内存泄漏，为什么threadlocal会造成内存泄漏？

什么是内存泄漏，为什么threadlocal会造成内存泄漏？

内存泄漏&#xff1a;指的是应用程序中存在无用的对象或者资源没有被垃圾回收机制回收&#xff0c;从而导致内存占用不断增加&#xff0c;最终导致应用程序的崩溃。 jvm里对象的引用按照从强到弱&#xff0c;分为四个强&#xff0c;软&#xff0c;弱&#xff0c;虚。强引用不会…
阅读更多...
YOLOv8改进实战 | 更换主干网络Backbone之PoolFormer篇

YOLOv8改进实战 | 更换主干网络Backbone之PoolFormer篇

目录 一、PoolFormer二、代码实现2.1 添加PoolFormer网络2.2 注册PoolFormer网络2.3 配置yaml文件yolov8-PoolFormer.yaml2.3 模型验证2.4 模型训练三、总结一、PoolFormer 2022 CVPR 论文链接：MetaFormer Is Actually What You Need for Vision Pytorch code：poolformer
阅读更多...
微信支付API

微信支付API

微信支付API 一、概念二、主要实现步骤 一、概念 主要经过小程序内调用登录接口、商户server调用支付统一下单、商户server调用再次签名&#xff0c;商户server接受支付通知&#xff0c;商户server查询支付结果。 二、主要实现步骤 1、小程序调用wx.login方法&#xff0c;获…
阅读更多...
AD9371 官方例程之 tx_jesd 与 xcvr接口映射

AD9371 官方例程之 tx_jesd 与 xcvr接口映射

文章目录 前言一、AD9371 ----> FMC_DP二、FMC_DP ----> FPGA_TX/RX三、rx_data_x and tx_data_x must be connected to the same channel四、ADRV9009 前言 axi_ad9371_tx_jesd --> util_ad9371_xcvr接口映射讲解 一、AD9371 ----> FMC_DP AD9371内部原理图 …
阅读更多...
oracle实现搜索不区分大小写

oracle实现搜索不区分大小写

<if test"code ! null and code ! ">and upper(code) like upper(%${code}%) </if>关键字upper
阅读更多...
简单了解一下：NodeJS的fs文件系统

简单了解一下：NodeJS的fs文件系统

NodeJS提供了fs模块来本地文件。大致有这些内容&#xff1a; 文件读写 在操作文件之前&#xff0c;我们需要检查一下这个文件是否存在&#xff0c;fs模块提供了access方法&#xff0c;语法如下&#xff1a;fs.access(path,mode,callback)。 path&#xff1a;就是文件路径&…
阅读更多...
最长上升子序列（二分）代码模板

最长上升子序列（二分）代码模板

用二分的思想求最长上升子序列的思想就是保持单调性&#xff0c;用一个q[]数组来作为一个单调数组。 每次将a[i]放进q数组中&#xff0c;但是要保持单调性&#xff0c;q数组的长度就是答案。 q[]数组中存的是所以以下标为长度的最长子序列的结尾的最小值。 理解q[]数组的意义…
阅读更多...
Python 机器学习入门之C4.5决策树算法

Python 机器学习入门之C4.5决策树算法

系列文章目录 第一章 Python 机器学习入门之线性回归 第一章 Python 机器学习入门之梯度下降法 第一章 Python 机器学习入门之牛顿法 第二章 Python 机器学习入门之逻辑回归 番外 Python 机器学习入门之K近邻算法 番外 Python 机器学习入门之K-Means聚类算法 第三章 Python 机…
阅读更多...
基于FPGA的图像拉普拉斯变换实现,包括tb测试文件和MATLAB辅助验证

基于FPGA的图像拉普拉斯变换实现,包括tb测试文件和MATLAB辅助验证

目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a vivado2019.2 3.部分核心程序 timescale 1ns / 1ps // // Company: // Engineer: // // Create Date: 202…
阅读更多...
GDB调试简单介绍

GDB调试简单介绍

最近和许多同事交流时&#xff0c;发现好多人只是在IDE上debug&#xff0c;但是gdb却一点都不了解&#xff1b;校招新来的同事更是都没听过gdb这个工具&#xff0c;所以在培训时给他们培训了一下&#xff1b;另外好久也没写blog了&#xff0c;刚好把这篇笔记简单分享一下。 0 …
阅读更多...
NetSuite SuiteWorld 2023观后感

NetSuite SuiteWorld 2023观后感

25年&#xff01;本周结束的SuiteWorld 2023是NetSuite的25周年庆。 下面两张照片分别来自1998年和今年。同样的人&#xff0c;同样的地点。左二是Evan&#xff0c;NetSuite的主要创始人。 当Evan展望未来25年后NetSuite这四位创始人的样子时。Evan GPT&#xff0c;给出了如下…
阅读更多...
XIlinx提供的DDR3 IP与 UG586

XIlinx提供的DDR3 IP与 UG586

DDR系统需要关注的三样东西&#xff1a;控制器、PHY、SDRAM颗粒&#xff0c;但这是实现一个DDR3 IP所需要的&#xff0c;如果只希望调用IP的话&#xff0c;则只需要调用IP即可&#xff0c;目前时间紧急&#xff0c;我先学一学如何使用IP&#xff0c;解决卡脖子的问题&#xff0…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023