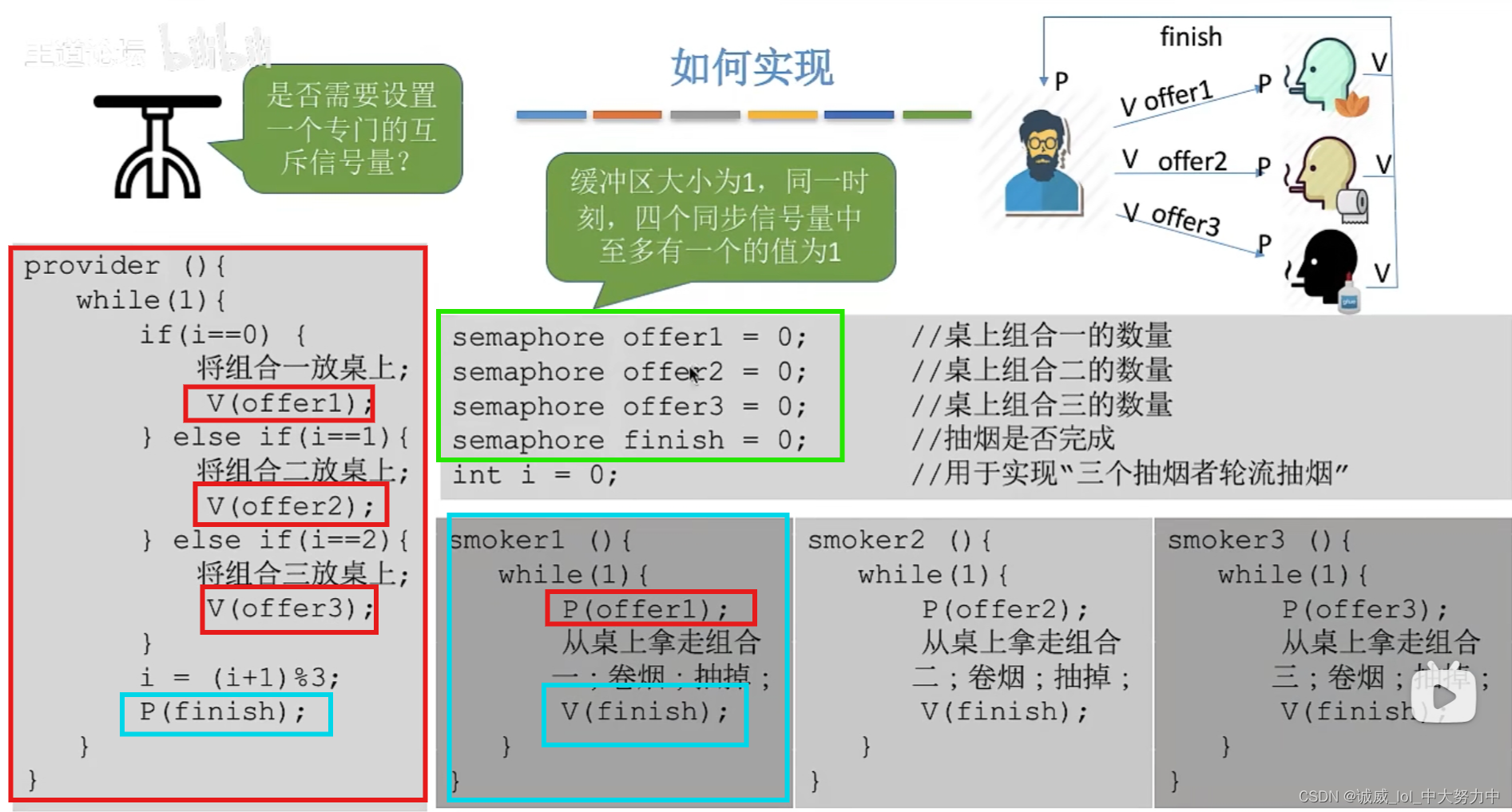
系列文章目录

第一章 Python 机器学习入门之线性回归
第一章 Python 机器学习入门之梯度下降法
第一章 Python 机器学习入门之牛顿法
第二章 Python 机器学习入门之逻辑回归
番外 Python 机器学习入门之K近邻算法
番外 Python 机器学习入门之K-Means聚类算法
第三章 Python 机器学习入门之ID3决策树算法
第三章 Python 机器学习入门之C4.5决策树算法

前言

之前说过ID3决策树算法存在的几个问题，而ID3的作者昆兰也在发布该算法不久后发现这些问题，于是提出了C4算法，后面有对C4升级变成了C4.5算法；而它之所以不叫ID4，ID5算法，是因为当时ID3算法发布后特别火，很多研究人员在ID3的基础上进行二次创新先提出了ID4、ID5算法，原作者就灵机一现，直接换了个新名称。

一、C4.5决策树详解

1、简介

从前言里面知道C4.5决策树的诞生就是为了解决之前ID3算法存在的问题，所以就直接说下它是如何解决问题的（注意一下，C4.5算法是在原有ID3算法基础上进行优化，虽然它可以解决特征值连续的问题，但是它仍然只用于分类问题上）。

2、连续特征值离散化

ID3决策树第一个问题，无法处理连续的特征值问题；假设样本里面某个特征F，它的取值为f1,f2,f3…,fn;C4.5算法会对依次取相邻两数的平均值，一共取得n-1个特征分类点；
将这些特征分类点假设作为样本的二元离散分类点，依次计算它们的信息增益，最后选取信息增益最大的特征划分点作为真正的二元离散分类点，这样就实现了连续特征值的离散化。

3、处理缺失数据

第二个问题，没办法对缺失数据进行处理；首先假设样本中某个特征F取值为f1、f2,先将二者的权重都设为1；然后查看样本中f1、f2特征无缺失样本，假设f1无缺失样本有3个，f2无缺失样本有7个，那么就将f1权重调整为3/10，f2权重调整为7/10;
因此样本特征值就是f1*3/10 和 f2 *7/10；后面计算信息增益和信息增益比使用该特征值计算即可。

4、降低对类别不平衡敏感

第三个问题：以信息增益作为划分训练数据集的特征时，存在于偏向于选择取值较多的特征的问题；就是分类结果容易被取值较多的特征影响；
因此引用信息增益比作为划分节点的标准，公式如下

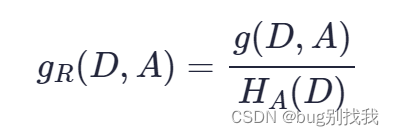
由于特征越多的特征对应的**特征熵Ha(D)越大，则信息增益比Gr(D,A)**则会变小，因此可以校正信息增益容易偏向于取值较多的特征的问题。

5、解决过拟合

决策树一般采用剪枝的方法解决过拟合问题，而C4.5则引入了正则化系数进行初步的剪枝

三、优缺点

1、优点

1. 易于理解和解释
2. 学习能力强

2、缺点

1. 只能用于分类问题
2. 不稳定,C4.5在数据微小变化下可能生成不同的树结构，这意味着它的结果在某种程度上不够稳定
3. 计算开销大,决策树的生成需要大量的熵值计算，并且如果特征值为连续值，还需要进行排序运算