AD9371 官方例程之 tx_jesd 与 xcvr接口映射

news2024/9/22 19:44:57

文章目录

前言
一、AD9371 ----> FMC_DP
二、FMC_DP ----> FPGA_TX/RX
三、rx_data_x and tx_data_x must be connected to the same channel
四、ADRV9009

前言

axi_ad9371_tx_jesd --> util_ad9371_xcvr接口映射讲解
在这里插入图片描述

一、AD9371 ----> FMC_DP

AD9371内部原理图
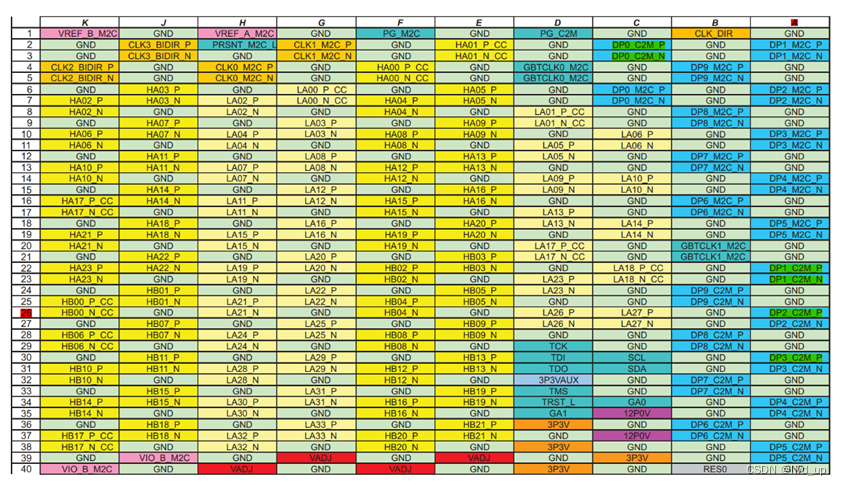
在这里插入图片描述

FMC链接
在这里插入图片描述
9371：
SERDIN0 ——> A26 27 ——> DP2_C2M
SERDIN1 ——> C2 C3 ——> DP0_C2M
SERDIN2 ——> A30 31 ——> DP3_C2M
SERDIN3 ——> A22 23 ——> DP1_C2M

SERDOUT0 ——> A2 3 ——> DP1_M2C
SERDOUT1 ——> A6 7 ——> DP2_M2C
SERDOUT2 ——> C6 7 ——> DP0_M2C
SERDOUT3 ——> A10 11 ——> DP3_M2C

二、FMC_DP ----> FPGA_TX/RX

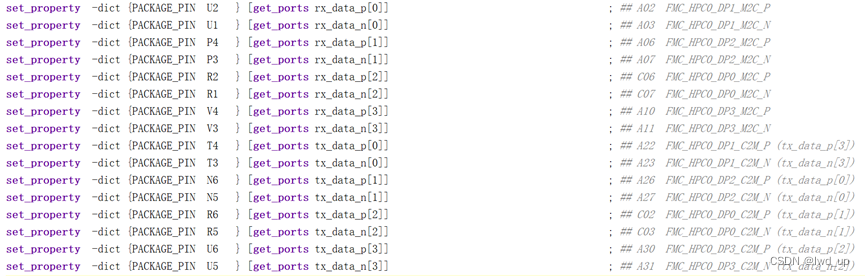
在这里插入图片描述
SERDIN0 ——> DP2_C2M ——> tx_data [1] ——> tx_1(xcvr) ——> tx_phy0(tx_jesd)
SERDIN1 ——> DP0_C2M ——> tx_data [2] ——> tx_2(xcvr) ——> tx_phy1(tx_jesd)
SERDIN2 ——> DP3_C2M ——> tx_data [3] ——> tx_3(xcvr) ——> tx_phy2(tx_jesd)
SERDIN3 ——> DP1_C2M ——> tx_data [0] ——> tx_0(xcvr) ——> tx_phy3(tx_jesd)

SERDOUT0 ——> DP1_M2C ——> rx_data [0] ——> rx_0(xcvr) ——> rx_phy0(rx_jesd)
SERDOUT1 ——> DP2_M2C ——> rx_data [1] ——> rx_1(xcvr) ——> rx_phy1(rx_jesd)
SERDOUT2 ——> DP0_M2C ——> rx_data [2] ——> rx_2(xcvr) ——> rx_phy2(rx_os_jesd)
SERDOUT3 ——> DP3_M2C ——> rx_data [3] ——> rx_3(xcvr) ——> rx_phy3(rx_os_jesd)

三、rx_data_x and tx_data_x must be connected to the same channel

在这里插入图片描述

    .tx_data_0_n (tx_data_n[0]),
    .tx_data_0_p (tx_data_p[0]),
    .tx_data_1_n (tx_data_n[1]),
    .tx_data_1_p (tx_data_p[1]),
    .tx_data_2_n (tx_data_n[2]),
    .tx_data_2_p (tx_data_p[2]),
    .tx_data_3_n (tx_data_n[3]),
    .tx_data_3_p (tx_data_p[3]),

可知t/rx_N_p/n 与 t/rx_data_N_p/n 和 tx_data_p/n[N] 一一映射

FPGA 与 FMC_DP 对应关系如下，每个 channel 对应相同的DP口，所以每个DP口连接相同的tx_data_p/n[N]即可符合要求

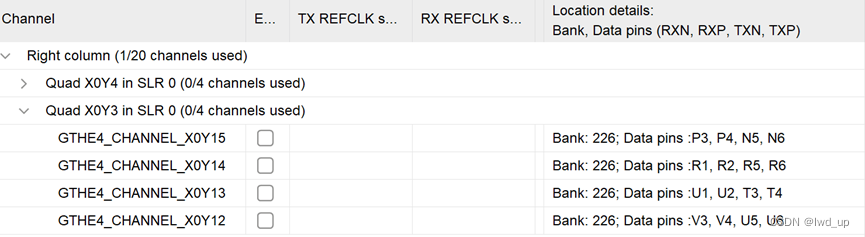
在这里插入图片描述

根据XDC文件

rx_data [0] ——> DP1_M2C | tx_data [0] ——> DP1_C2M
rx_data [1] ——> DP2_M2C | tx_data [1] ——> DP2_C2M
rx_data [2] ——> DP0_M2C | tx_data [2] ——> DP0_C2M
rx_data [3] ——> DP3_M2C | tx_data [3] ——> DP3_C2M

每个DP口连接相同的tx_data_p/n[N]，符合 connected to the same channel

四、ADRV9009

ADRV 9009 与 AD9371 类似
AD9009内部原理图
在这里插入图片描述
SERDIN0 ——> A22 23 ——> DP1_C2M
SERDIN1 ——> A30 31 ——> DP3_C2M
SERDIN2 ——> C2 C3 ——> DP0_C2M
SERDIN3 ——> A26 27 ——> DP2_C2M

SERDOUT ADRV9009 与 AD 9371相同

9009 XDC 文件
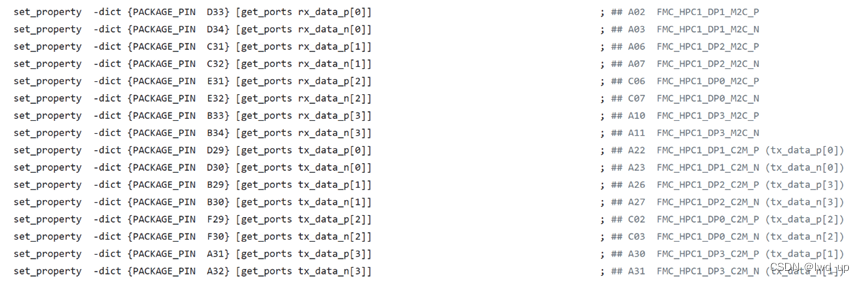
在这里插入图片描述
SERDIN0 ——> DP1_C2M ——> tx_data [0] ——> tx_0 ——> tx_phy0
SERDIN1 ——> DP3_C2M ——> tx_data [3] ——> tx_3 ——> tx_phy1
SERDIN2 ——> DP0_C2M ——> tx_data [2] ——> tx_2 ——> tx_phy2
SERDIN3 ——> DP2_C2M ——> tx_data [1] ——> tx_1 ——> tx_phy3