扩散模型是跨不同深度学习领域使用的生成模型。目前，它们主要用于图像和音频生成。最值得注意的是，这些模型是令人印象深刻的图像生成模型（例如 Dalle2 和稳定扩散）背后的驱动力。我相信您已经看过这些模型生成的闪烁图像。令人惊叹的结果证明了深度学习的进步是多么令人兴奋。

什么是Diffusion？

在物理学中，扩散只是任何事物的整体运动。 （原子，能量）从较高浓度的区域到较低浓度的区域。现在想象一下，将一小滴油漆滴入一杯水中，油漆的密度将集中在一个位置，但随着时间的推移，该滴将扩散到水中直至达到平衡。如果我们能逆转这个过程不是很好吗？不幸的是，这是不可能的。但扩散模型试图拟合一个模型，其最终目标是逆转这一过程。

其基本思想是通过迭代前向扩散过程系统地、缓慢地破坏数据分布中的结构。然后，我们学习反向扩散过程，恢复数据结构，产生高度灵活且易于处理的数据生成模型。

扩散模型尝试通过向原始图像迭代添加噪声来重现扩散过程。我们不断添加噪声，直到图像变成纯噪声。噪声由马尔可夫事件链定义。马尔可夫链是一种事件模型，其中每个时间步仅取决于前一个时间步。马尔可夫性质定义如下：

P(Xₙ = iₙ | Xₙ₋₁)

因此，任意满足上述条件的随机变量序列X₀，X₁，X2，…，Xₙ都可以被视为马尔可夫链。这种马尔可夫假设使得学习添加的噪声变得容易处理。在训练模型来预测每个时间步的噪声后，该模型将能够从高斯噪声输入生成高分辨率图像。总结一下：我们不断向图像添加噪声，直到只剩下纯粹的噪声。然后我们训练一个神经网络来消除噪音。因此扩散模型由两个阶段组成：

1. 前向扩散过程
2. 逆扩散过程

前向扩散过程

前向扩散过程是数据结构被破坏的阶段。这是通过应用从正态分布采样的噪声来完成的 - 最终图像随后将收敛到纯噪声 z ~ N(0, 1)。每个时间戳应用的噪声量不是恒定的。使用时间表来缩放平均值和方差。 OpenAI 的原始 DDPM 论文应用了线性调度。但 OpenAI 的研究人员再次发现，这会导致许多冗余的扩散步骤。因此，在他们的《改进的去噪扩散概率模型》论文中，他们实现了自己的余弦计划。

前向过程定义为 q(xₜ|xₜ₋₁)。该函数只是在每个时间步 t 添加噪声。前向过程的数学定义如下：q(xₜ|xₜ₋₁) = N(xₜ; sqrt{1-βₜ}xₜ, βₜI)。您可能还记得在统计课上，正态分布是由均值和方差参数化的。 sqrt{1-βₜ}xₜ 是平均值。 βₜI 是方差。您在此等式中看到的 beta 只是范围在 0–1 之间的值 0<β₁<β2<…<β_T<1；贝塔值并不是恒定的，并且受“方差表”的调节。通常，您希望对每个时间步 t 重复此过程。只需一步即可完成这一过程将为我们节省大量计算量。让我们看看它是如何完成的。首先，我们定义 αₜ = 1-βₜ。然后我们可以定义所有 alpha 的累积乘积 α⁻ₜ = ∏aₛ 现在，使用重新参数化技巧，我们可以将上述公式重写如下：

使用 alpha，我们可以将其重写为：

正如您所猜测的，我们现在可以将其扩展到之前的时间步骤：

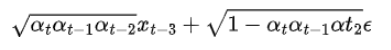
使用所有 alpha 的乘积，最终方程将采用以下形式：

逆扩散过程

如果通过计算 q(xₜ₋₁|xₜ) 来反转上述过程，那就太好了。不幸的是，这个计算需要每个时间步长。因此，我们恢复到学习近似这些条件概率的神经模型。在相反的过程中，神经网络将预测给定图像的平均值。神经网络将查看图像并尝试确定前向过程中该图像来自的图像分布。

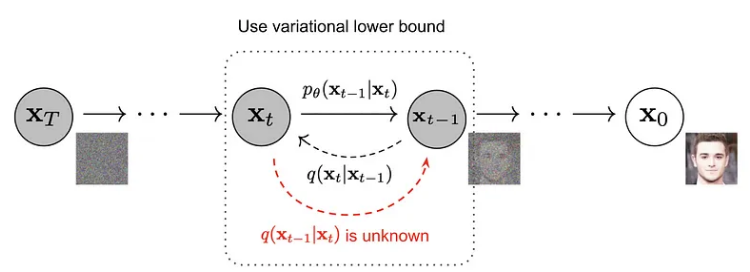
我们的扩散模型损失函数就是 -log(pθ(x₀))。问题在于扩散模型是潜变量模型，其形式如下：

正如你所想象的，这种形式没有封闭的解决方案。解决这个问题的方法是计算变分下界。请注意，了解 VAE 的推导可以帮助您理解以下公式。整个逆过程定义为：

由于这是联合分布，我们必须将每个逆过程相乘。请记住，pθ(xₜ₋₁|xₜ) 将您从“噪声较大”的图像变为“噪声较小”的图像。我提到了变分下界，但它是什么？在较高的层面上，假设我们有一个难以处理的函数 f(x)。如果我们能证明我们有一个小于 f(x) 的函数 g(x)。然后通过最大化 g(x)，我们可以确定 f(x) 也会增加。让我们通过将 KL 散度添加到原始函数 f(x) = -log(pθ(x₀)) 来比较 -log(pθ(x₀))。

通过贝叶斯定理重写KL散度，我们得到：

所以我们的变分下界变成：

我们现在的目标是将右侧转换为可分析计算的。让我们首先将日志重写为产品：

使用对数乘积法则，我们可以重写右侧：

取出求和的第一项，得到以下结果：

使用贝叶斯定理重写 q(xₜ|xₜ₋₁) 并在 t = 0 时对输入图像进行调节：

替代

使用乘积法则：

第二个求和可以进一步简化。取 T 等于任何数字，您会发现大部分项都被抵消了，您将得到以下结果：

替换

使用商规则，我们可以重写最后两项：

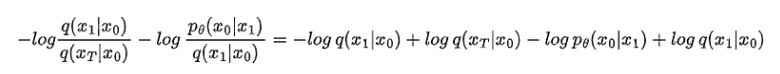
您可以看到第一项和最后一项相互抵消。使用商规则的另一种用法来整理我们的公式：

我们现在可以写出 KL 散度的对数项：

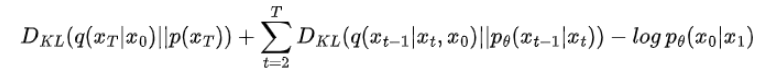
DDPM 论文的作者忽略了第一项。如上所述，项 pθ(xₜ₋₁|xₜ) 可以重写为预测均值的神经网络：

q(xₜ₋₁|xₜ, x₀) 具有如前所述的闭式解。我们可以将其写为：

作者在实际 μ 和预测 μ 之间采用了简单的均方误差。他们使用超出本博客文章范围的定义来证明，得出以下结论：

使用上面的定义，我们可以将均方误差简化为：

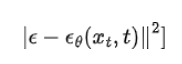
这就是我们采取梯度下降步骤的术语！所有这些简化，我们得出以下结论：预测噪声。最终的目标函数采用以下形式：

什么是 Stable Diffusion？

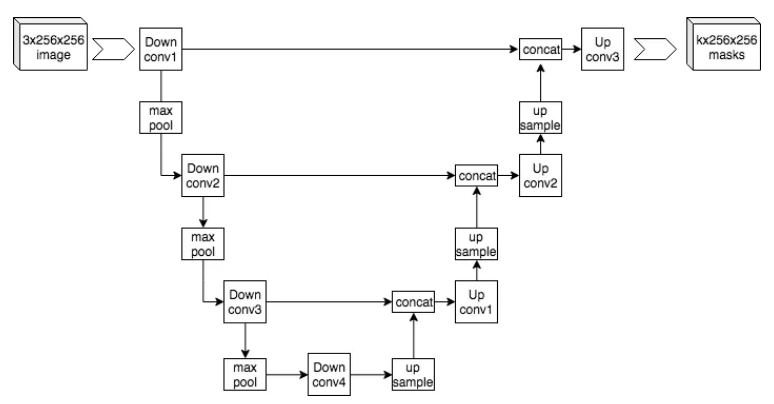
稳定扩散是 OpenAI Dalle.2 的开源替代品。由于稳定扩散是一种潜在扩散模型，因此我将尝试对 LDM 进行高级解释。还记得反向扩散过程如何使用神经网络逐渐降低噪声吗？稳定扩散使用 U-Net，这是一种基于卷积的神经网络，可将图像下采样到较低的维度，并在上采样期间重建它。在下采样层和上采样层之间添加跳跃连接以获得更好的梯度流。通过将从语言模型生成的文本嵌入连接到图像表示，将提示注入到模型中。 U-Net 中的注意力层允许模型通过交叉注意力来关注文本标记。

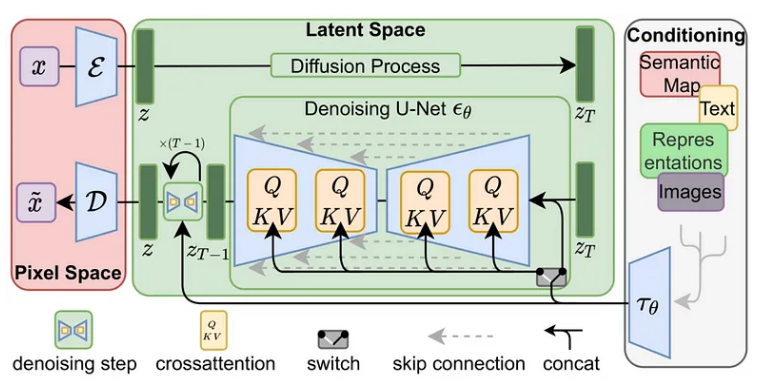
顾名思义，LDM 不适用于原始像素。相反，图像通过编码器被编码到更小的空间中。然后通过解码器将图像解码回其原始空间。这允许扩散过程在小/潜在空间上工作并完成该空间中的去噪。您可以将其视为包含扩散过程的自动编码器。这就是为什么它被称为潜在扩散；我们不是在像素中而是在潜在空间中实现扩散过程。下图应该足以概括 LDM：

总结

1. 扩散模型的工作原理是迭代地向图像添加噪声，然后训练神经网络来学习噪声并恢复图像。
2. U-Net 是逆向过程中使用最广泛的神经网络。
3. U-Net 中添加了跳过连接和注意力层以获得更好的性能。
4. LDM 的工作原理是将图像编码到较小的潜在空间并在该空间中实现扩散过程，然后通过解码器恢复图像。