1 Self-attention的特点

self-attention是一种通过自身和自身进行关联的attention机制, 从而得到更好的representation来表达自身.

self-attention是attention机制的一种特殊情况，在self-attention中, Q=K=V, 序列中的每个单词(token)都和该序列中的其他所有单词(token)进行attention规则的计算.

attention机制计算的特点在于, 可以直接跨越一句话中不同距离的token, 可以远距离的学习到序列的知识依赖和语序结构.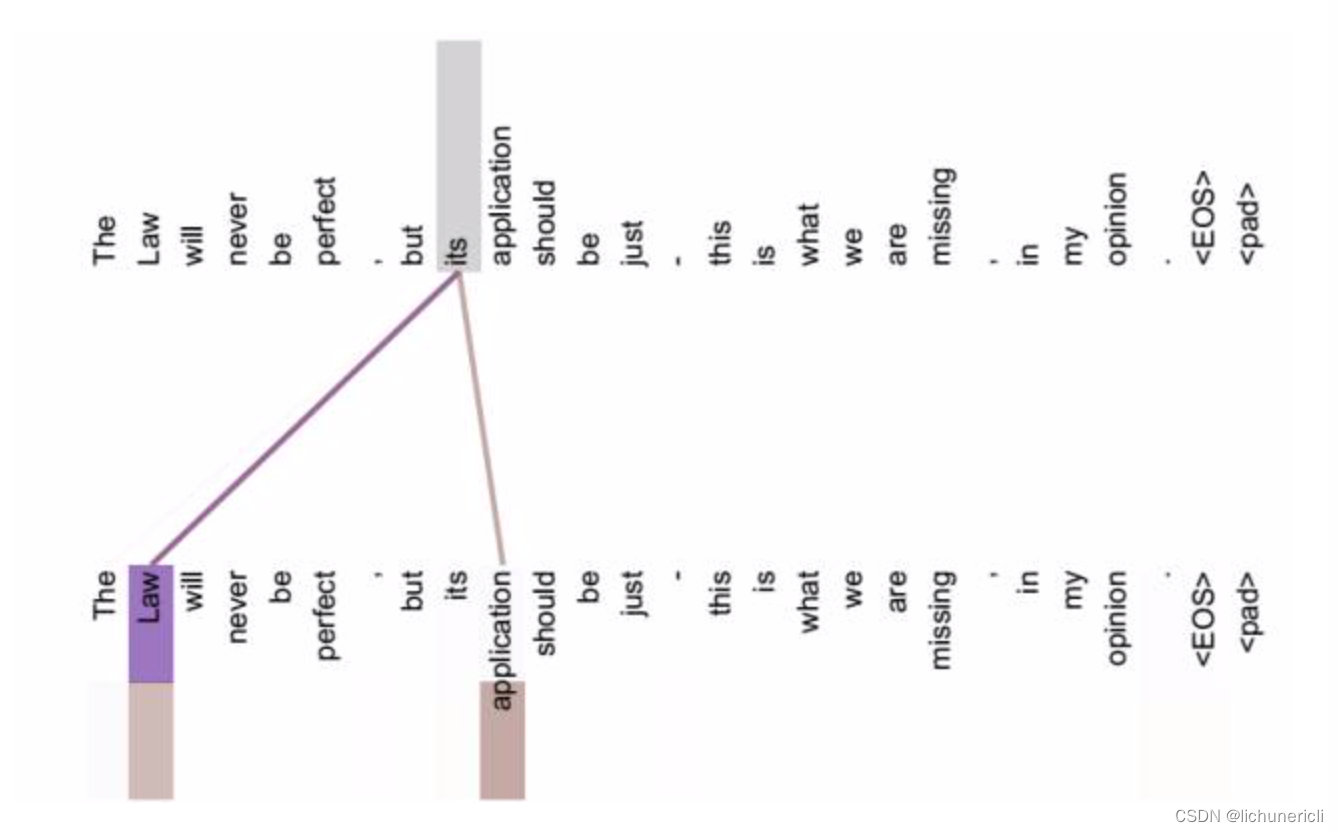

• 从上图中可以看到, self-attention可以远距离的捕捉到语义层面的特征(its的指代对象是Law)。

• 应用传统的RNN, LSTM, 在获取长距离语义特征和结构特征的时候, 需要按照序列顺序依次计算, 距离越远的联系信息的损耗越大, 有效提取和捕获的可能性越小。

• 但是应用self-attention时, 计算过程中会直接将句子中任意两个token的联系通过一个计算步骤直接联系起来。

关于self-attention为什么要使用(Q, K, V)三元组而不是其他形式：

• 首先从分析的角度看，查询Query是一条独立的序列信息，通过关键词Key的提示作用，得到最终语义的真实值Value表达，数学意义更充分，完备。
• 不使用(K, V)或者(V)没有什么必须的理由，也没有相关的论文来严格阐述比较试验的结果差异，所以可以作为开放性问题未来去探索，只要明确在经典self-attention实现中用的是三元组就好。

2 Self-attention中的归一化概述

• 训练上的意义: 随着词嵌入维度d_k的增大, q * k 点积后的结果也会增大, 在训练时会将softmax函数推入梯度非常小的区域, 可能出现梯度消失的现象, 造成模型收敛困难.

• 数学上的意义: 假设q和k的统计变量是满足标准正态分布的独立随机变量, 意味着q和k满足均值为0, 方差为1. 那么q和k的点积结果就是均值为0, 方差为d_k, 为了抵消这种方差被放大d_k倍的影响, 在计算中主动将点积缩放1/sqrt(d_k), 这样点积后的结果依然满足均值为0, 方差为1.

3 softmax的梯度变化

这里我们分3个步骤来解释softmax的梯度问题:

• 第一步: softmax函数的输入分布是如何影响输出的.
• 第二步: softmax函数在反向传播的过程中是如何梯度求导的.
• 第三步: softmax函数出现梯度消失现象的原因.

3.1 softmax函数的输入分布是如何影响输出的

• 对于一个输入向量x, softmax函数将其做了一个归一化的映射, 首先通过自然底数e将输入元素之间的差距先"拉大", 然后再归一化为一个新的分布. 在这个过程中假设某个输入x中最大的元素下标是k, 如果输入的数量级变大(就是x中的每个分量绝对值都很大), 那么在数学上会造成y_k的值非常接近1.
• 具体用一个例子来演示, 假设输入的向量x = [a, a, 2a], 那么随便给几个不同数量级的值来看看对y3产生的影响

a = 1时,   y3 = 0.5761168847658291
a = 10时,  y3 = 0.9999092083843412
a = 100时, y3 = 1.0

• 采用一段实例代码将a在不同取值下, 对应的y3全部画出来, 以曲线的形式展示:

from math import exp
from matplotlib import pyplot as plt
import numpy as np 
f = lambda x: exp(x * 2) / (exp(x) + exp(x) + exp(x * 2))
x = np.linspace(0, 100, 100)
y_3 = [f(x_i) for x_i in x]
plt.plot(x, y_3)
plt.show()

• 得到如下的曲线:
• 

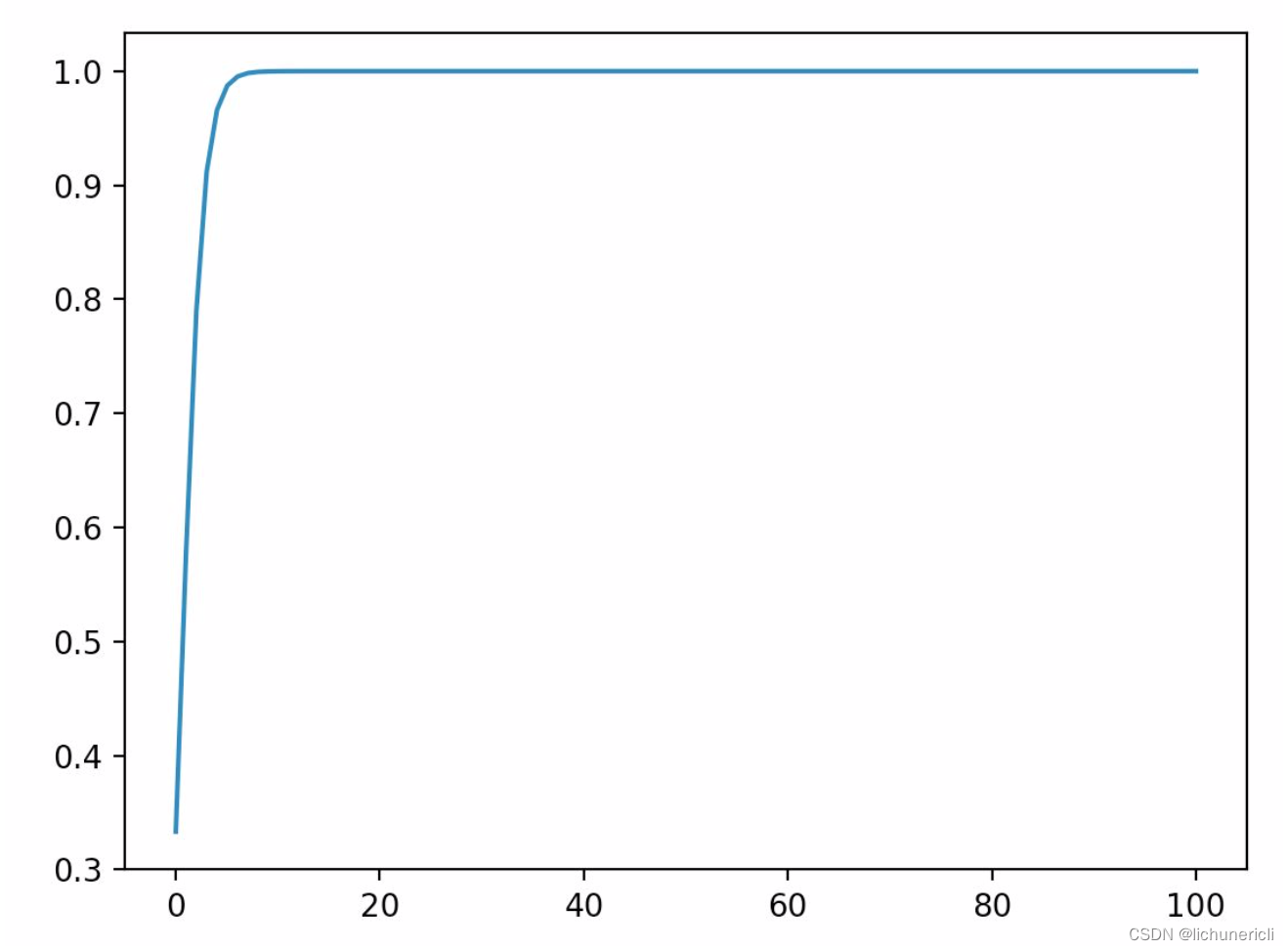
• 从上图可以很清楚的看到输入元素的数量级对softmax最终的分布影响非常之大.

• 结论: 在输入元素的数量级较大时, softmax函数几乎将全部的概率分布都分配给了最大值分量所对应的标签.

3.2 softmax函数在反向传播的过程中是如何梯度求导的

首先定义神经网络的输入和输出:

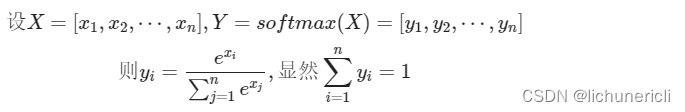
反向传播就是输出端的损失函数对输入端求偏导的过程, 这里要分两种情况, 第一种如下所示:

第二种如下所示:

经过对两种情况分别的求导计算, 可以得出最终的结论如下:

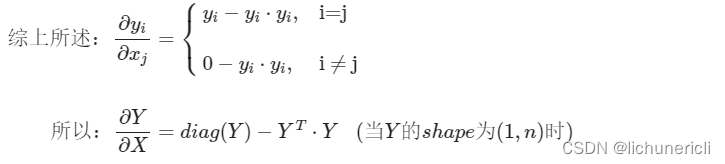
3.3 softmax函数出现梯度消失现象的原因

• 根据第二步中softmax函数的求导结果, 可以将最终的结果以矩阵形式展开如下:

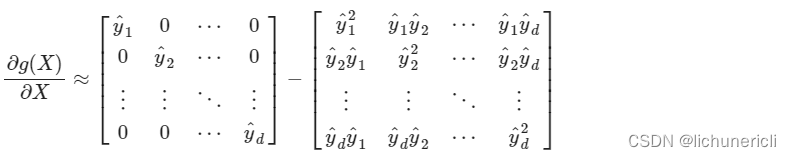
• 根据第一步中的讨论结果, 当输入x的分量值较大时, softmax函数会将大部分概率分配给最大的元素, 假设最大元素是x1, 那么softmax的输出分布将产生一个接近one-hot的结果张量y_ = [1, 0, 0,..., 0], 此时结果矩阵变为:

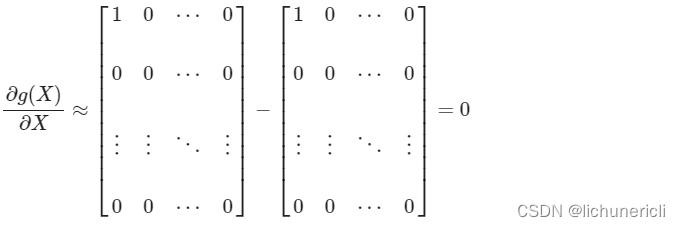
• 结论: 综上可以得出, 所有的梯度都消失为0(接近于0), 参数几乎无法更新, 模型收敛困难.

4 维度与点积大小的关系

• 针对为什么维度会影响点积的大小, 原始论文中有这样的一点解释如下:

To illustrate why the dot products get large, assume that the components of q and k 
are independent random variables with mean 0 and variance 1. Then their doct product,
q*k = (q1k1+q2k2+......+q(d_k)k(d_k)), has mean 0 and variance d_k.

• 分两步对其进行一个推导, 首先就是假设向量q和k的各个分量是相互独立的随机变量, X = q_i, Y = k_i, X和Y各自有d_k个分量, 也就是向量的维度等于d_k, 有E(X) = E(Y) = 0, 以及D(X) = D(Y) = 1.

• 可以得到E(XY) = E(X)E(Y) = 0 * 0 = 0

• 同理, 对于D(XY)推导如下:

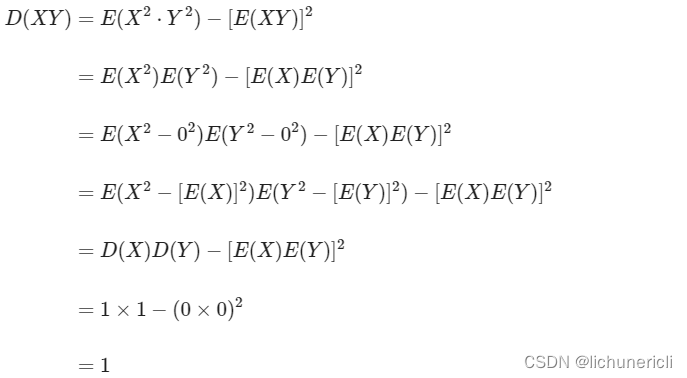
• 根据期望和方差的性质, 对于互相独立的变量满足下式:

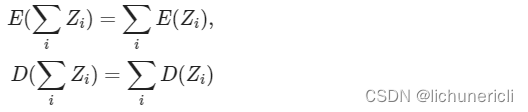
• 根据上面的公式, 可以很轻松的得出q*k的均值为E(qk) = 0, D(qk) = d_k.

• 所以方差越大, 对应的qk的点积就越大, 这样softmax的输出分布就会更偏向最大值所在的分量.

• 一个技巧就是将点积除以sqrt(d_k), 将方差在数学上重新"拉回1", 如下所示:

• 最终的结论: 通过数学上的技巧将方差控制在1, 也就有效的控制了点积结果的发散, 也就控制了对应的梯度消失的问题!