一、说明
线性模型很棒,因为它们易于理解且易于优化。他们受苦是因为他们只能学习非常简单的决策边界。神经网络可以学习更复杂的决策边界,但失去了线性模型良好的凸性特性。
使线性模型表现出非线性的一种方法是转换输入。例如,通过添加特征对作为附加输入。在这种表示上学习线性模型是凸的,但在除了非常低维的空间之外的所有空间中,计算量都是令人望而却步的。有人可能会问:是否可以保留原始数据表示,而不是显式扩展特征空间,并且所有特征都会破坏隐式?令人惊讶的是,答案通常是“是”,而使这成为可能的技术系列被称为内核方法。
二、从特征组合到内核
增加线性模型表达能力的一种方法是爆炸特征空间。例如,“二次”特征爆炸可能会将特征向量x = <x_1, x_2,x_3,…,x_D> 映射到表示为 φ(x) 的扩展版本:
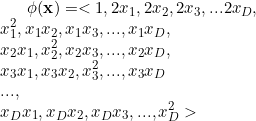
然后我们可以在扩展的特征空间上训练分类器。这样做有两个主要问题。第一个是计算性的:如果您的线性算法在特征数量上线性扩展,那么您只需对需要执行的计算量进行平方即可;您还计算了所需内存量的平方。第二个是统计方面的:如果您按照启发式,每个特征应该有大约两个示例,那么您现在将需要二次方数量的训练示例,以避免过度拟合。
我们将在这篇文章中尝试解决计算问题。
基于内核的学习的关键见解是,您可以以不需要显式计算 φ( x) 的方式重写许多线性模型。首先,您可以将其视为纯粹的计算“技巧”,使您能够使用二次特征映射的强大功能,而无需实际计算和存储映射向量。稍后你会发现它更深一些。我们讨论的大多数算法在执行特征映射后都涉及w · φ( x )形式的乘积。目标是重写这些算法,以便它们只依赖于两个示例(例如x和z)之间的点积;即,它们取决于 φ( x ) · φ( z )。要理解为什么这很有用,请考虑上面的二次展开和两个向量之间的点积。你得到:
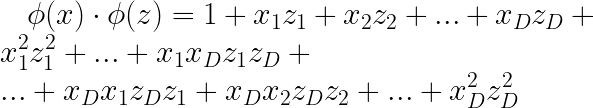

![]()
![]()
因此,计算 φ( x ) · φ( z ) 所需的时间与计算x · z所用的时间完全相同(加上执行加法和乘法所需的时间)。
其余的实际挑战是重写算法,以便它们依赖于示例之间的点积,而不是任何显式的权重向量。
三、核化感知器
让我们考虑上一篇文章中的原始感知器算法,这里使用线性代数符号和特征扩展符号 φ(x ) 进行重复。
PerceptronTrain(D,MaxIter)
w <- 0 // initialize weights
b <- 0 // initialize bias
for iter=1 to MaxIter do
for all (x,y) ∈ D do
a ← w · φ( x) + b // compute activation for this example
if ya <= 0 then
w ← w + y φ(x ) // update weights
b <- b + y // update bias
endif
endfor
endfor
return w, b
在这个算法中,有两个地方明确使用了φ( x ) 。第一个是计算激活(第 4 行),第二个是更新权重(第 6 行)。目标是消除该算法对 φ 和权重向量的显式依赖。
为此,您可以观察到在算法中的任何点,权重向量w都可以写成扩展训练数据的线性组合。特别是,在任意点,对于某些参数 α, w = Σ α_nφ(x_n)。最初,w = 0,因此选择α = 0 会产生此结果。如果第一次更新发生在第 n 个训练样本上,则分辨率权重向量就是 y_n φ(x_n),相当于设置 α_n = y_n。如果第二次更新发生在第 m 个训练样本上,那么您所需要做的就是更新 α_m ← α_m + y_m。这一观察结果引出了以下表示定理,该定理指出感知器的权重向量位于训练数据的范围内。
感知器表示定理:在感知器算法运行期间,权重向量w始终位于(假设非空)训练数据φ(x_1 ), 的范围内。。。, φ (x_N)。
证明。通过归纳法。基本情况:任何非空集的跨度都包含零向量,即初始权重向量。归纳情况:假设定理在第 k 次更新之前为真,并假设第 k 次更新发生在示例 n 上。根据归纳假设,可以在更新前写出w = Σ α_i φ(x_i) 。新的权重向量为 [Σ α_i φ(x_i )] + y_n φ( x_n ) = Σ (α_i + y_n [ i = n])φ (x_i ),仍然在训练数据的范围内。
并不是说我们知道对于某些 α_is 总是可以写出w = Σα_nφ(x_n),我们还可以将激活(第 4 行)计算为:
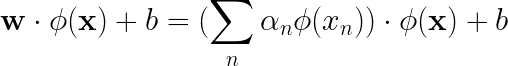

现在,这仅取决于数据点之间的点积,并且从不明确需要权重向量。您现在可以重写整个感知器算法,以便它永远不会明确引用权重,而仅依赖于示例之间的成对点积
这种“核化”算法的优点是,您可以“免费”执行特征扩展,例如简介中的二次特征扩展。例如,对于与二次特征完全相同的成本,您可以使用三次特征图,计算为 φ( ̈ x)φ(z) = (1 + x · z)³,它对应于变量之间的三向交互。(而且,一般来说,您可以在相同的计算复杂度下对任何多项式次数 p 执行此操作。)
四、什么构成了内核?
内核只是广义点积的一种形式。您也可以将其视为 φ( x ) · φ( z ) 的简单简写。这通常称为xa和z之间的内核乘积。
从这个角度来看,我们在上一节中看到的是,您可以重写感知器算法(这同样适用于许多其他算法),以便它们仅依赖于数据点之间的内核乘积,而不依赖于实际数据点他们自己。这是一个非常强大的概念,因为它使得大量非线性算法的开发基本上“免费”(通过应用所谓的内核技巧)。
4.1 核函数的特点
机器学习(包括 SVM(支持向量机))中使用的核函数具有几个重要特征,包括:
- Mercer 条件:核函数必须满足 Mercer 条件才有效。这个条件确保核函数是半正定的,这意味着它总是大于或等于零。
- 正定性:如果核函数始终大于零(除非输入彼此相等),则该核函数是正定的。
- 非负性:核函数是非负的,这意味着它为所有输入生成非负值。
- 对称性:核函数是对称的,这意味着无论输入的顺序如何,它都会产生相同的值。
- 再现性:如果核函数可以用来重建特征空间中的输入数据,则它满足再现性。
- 平滑度:如果核函数能够将输入数据平滑地变换到特征空间,则称该核函数是平滑的。
- 复杂性:核函数的复杂性是一个重要的考虑因素,因为更复杂的核函数可能会导致过度拟合并降低泛化性能。
基本上,核函数的选择取决于具体问题和数据的特征,选择合适的核函数可以显着影响机器学习算法的性能。
4.2 内核函数
核是用于将原始输入数据点映射到高维特征空间的数学函数,因此,即使数据点在原始输入空间中不是线性可分的,也可以轻松找到超平面。一些常见的核函数包括线性核函数、多项式核函数、径向基函数 (RBF) 和 sigmoid 核函数。
标准核函数方程:
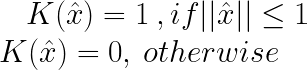
高斯核:
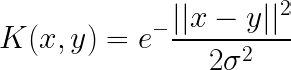
高斯核用于在没有数据先验知识的情况下执行变换。
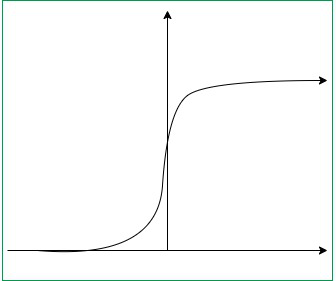
sigmoid函数:
该函数相当于神经网络的第二层感知器模型l,用作人工神经元的激活函数。
![]()
五、结论
弗朗西斯科·佛朗哥