【数据结构与算法篇】还不会二分查找？看这篇就够了！

👻内容专栏：《数据结构与算法篇》
🐨本文概括：整数二分算法（朴素二分，查找区间左端点与区间右端点二分）、浮点数二分
🐼本文作者：阿四啊
🐸发布时间：2023.10.22

- 二分查找(binary search)
- - 1.朴素二分查找：
  - - 代码实现：
  - 2.二分查找优化
  - - 查找区间的左端点
    - - ⚠️细节问题处理：
      - 一、循环条件问题
        二、求中点(mid)问题
    - 查找区间的右端点
    - - ⚠️细节问题处理：
      - 一、循环条件问题：
        二、求中点(mid)问题：
    - 二分模板总结
    - 代码实现：
  - 3.浮点数二分
- References

二分查找(binary search)

1.朴素二分查找：

704. 二分查找 - 力扣（LeetCode）

以上这一题可以利用暴力的方式，将数组遍历一遍，查找target的位置，时间复杂度为O(n)，那么有没有高效的算法呢？

二分查找算法：时间复杂度为O(logN)，前提认为数组为有序序列(单调性)即可(其实后面学习，前提并不是数组为单调性，而是区间具有二段性，也就是说按某种性质，可以将该数组分为两段区间)。

📌ps：那么假设一共4,294,967,296(2^32)个数据，暴力枚举的时间复杂度为4* 10^9 ，而二分查找就只需要32次了。

我们来看一张二分查找与遍历查找的效率对比图：

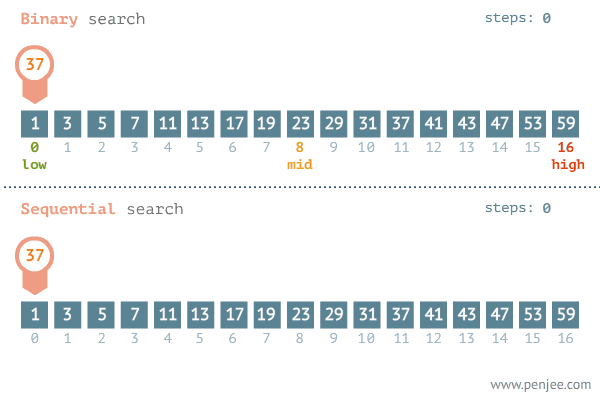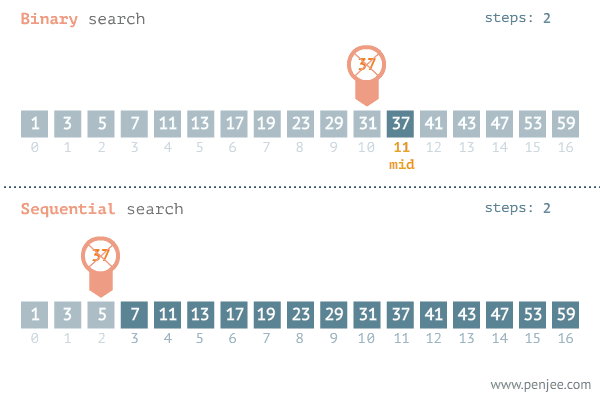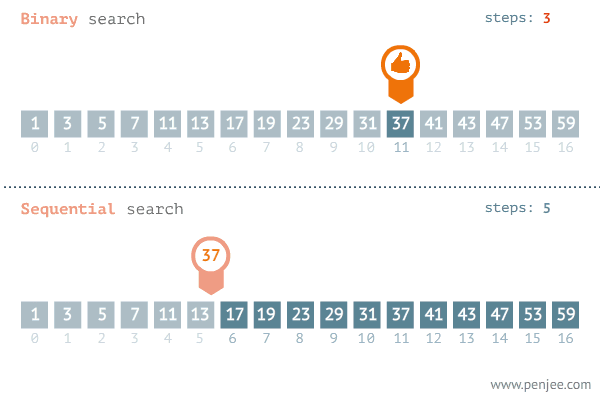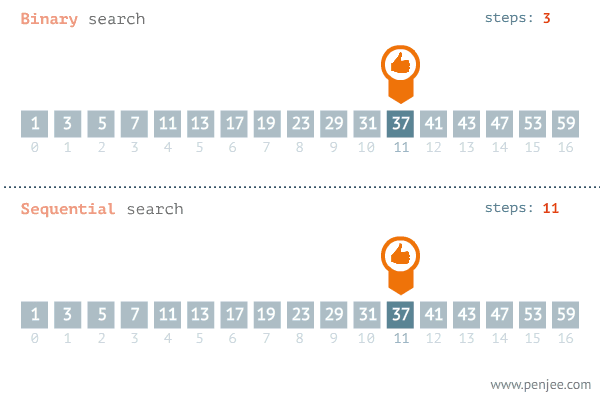
代码实现：

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0, right = nums.size() - 1;
        while(left <= right)
        {
            int mid = left + (right - left) / 2; //防止溢出
            if(target < nums[mid]) right = mid - 1;
            else if(target > nums[mid]) left = mid + 1;
            else return mid;
        }
        return -1;
    }
};

2.二分查找优化

34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）

题目描述：

在这里插入图片描述

📌假设1,2,3,3,3,4,5这组数据，目标值为3，找到目标值在数组中的开始下标和结束下标。显然用朴素二分去做就很棘手了，因为并不能确定3是在起始位置还是终点位置，若在中间位置呢，还另外需要向前遍历向后遍历等于3的值，若极端的情况之下，变成3,3,3,3,3,3,3这组数据，那么朴素的二分就退化为暴力求解的时间复杂度了，在这里会讲解查找区间左端点（简称Search_Left）和查找区间右端点（简称Search_Right）两个模板，根据结论记住模板即可，这里的记忆并不是死记硬背，而是需要理解边界处理的细节过程！！！

查找区间的左端点

🎗️以下target简述为t

假设我们需要先查找区间的左端点，那么端点左边的区域1,2一定是小于t的，端点右边区域包括该端点3,3,3,4,5大于等于t的。

在这里插入图片描述

假设算出的mid下标所对应的元素为x；
x < t，那么x肯定是在小于t的区间里，t在x的右边，此时left需要更新为mid+1，然后再到[left,right]区间中继续查找；
```
if(x < t) left = mid + 1;
```
若x ≥ t，即 [mid, right]区域里的元素肯定是大于等t的，那么此时right需要更新为mid，然后再到[left,right]区间中继续查找；
```
if(x >= t) right = mid;
```

在这里插入图片描述

⚠️细节问题处理：

以上为查找区间左端点的核心步骤了，但是重点是两处细节处理操作。

一、循环条件问题

这里的循环继续条件是，像朴素二分查找一样left <= right 还是left < right呢？答案是**left < right**，我们看以下分析：

为了保证说服力，我们假设给出三种情况的数据：1.数组中有结果（等于t的值）、2.数组中全是大于t的值、3.数组中全是小于t的值

1.数组中有结果（图中这个结果ret为本次区间需要求的左端点t）。

先看我们的right，前面说过，x ≥ t时，我们的right一定是在ret右边的区间里移动。x < t时，left执行的是left = mid + 1。等到left继续走之后，也就是left == right，此时指向的ret就是我们想要的结果。所以无需判断left == right的情况。
2.数组中全是大于t的值

数组中left指针指向的元素一定是大于t的，那么此时，我们的right会走前面第二种情况，一直执行right = mid操作，right指针会向前移动，等到left == right时，跳出循环，判断此时的left or right是否等于t，是的话就返回结果，否则返回{-1，-1}即可。
3.数组中全是小于t的值

数组中right指针指向的元素一定是小于t的，那么此时，left会执行前面第一种情况，一直执行left = mid + 1操作，left会向后移动，等到left == right时，跳出循环，判断此时的left or right是否等于t，是的话就返回结果，否则返回{-1，-1}即可。

在这里插入图片描述

所以，循环条件为left < right我们无需进行left == right相等的情况，若判断，就会出现死循环。

二、求中点(mid)问题

查找区间左端点中我们求mid应该使用left + (right - left) / 2向下取整，而不是 left + (right - left + 1) / 2向上取整。为什么呢？

假定为向上取整，会发生什么情况？下面我们来分析一下：

假如数组中只有两个元素，我们使用向上取整的方式求mid，此时mid会指向第二个元素，当程序走第二种情况right = mid，就会陷入死循环！

在这里插入图片描述

查找区间的右端点

假设我们需要先查找区间的右端点，那么端点左边区域包括该端点1,2,3,3,3小于等于t的，端点右边的区域4, 5一定是大于t的。
在这里插入图片描述

同样的，我们假设算出的mid下标所对应的元素为x；
当x <= t，说明x是在小于等于t的区间里，此时我们需要变动left，x因为也可能会等于t，所以更新为left = mid，然后再到[left,right]区间中继续查找；
```
if(x <= t) left = mid
```
当x > t，说明x是落在大于t的区间里面，此时我们需要变动right，t至少为落在该区间的左边位置，所以更新为right = mid - 1，然后再到[left,right]区间中继续查找；
```
if(x > t) right = mid - 1;
```

在这里插入图片描述

⚠️细节问题处理：

一、循环条件问题：

这里像找左端点的循环条件一样，也是left < right ，就不多说了。

二、求中点(mid)问题：

查找区间右端点中我们求mid应该使用 left + (right - left + 1) / 2向上取整，而不是left + (right - left) / 2向下取整。

假定为向下取整，会发生什么情况？下面我们来分析一下：

假如数组中只有两个元素，我们使用向下取整的方式求mid，此时mid会指向第一个元素，当程序走第一种情况left = mid，就会陷入死循环！
在这里插入图片描述

二分模板总结

🚩：以下是二分模板的总结，关于二分查找的模板我们最好去理解它，分类讨论，根据不同的题目场景去应用，而不是死记硬背。

🔗Get验证技巧：有(右)加必有(右)减，此口诀针对的是右端点模板，右加是求中点时+1，右减是代码过程里有-1。

在这里插入图片描述

代码实现：

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        //特判一下
        if(nums.size() == 0) return {-1, -1};
         
        int left = 0, right = nums.size() - 1;
        while(left < right)
        {
            int mid = left + (right - left) / 2;
            if(nums[mid] < target) left = mid + 1;
            else right = mid;
        }
        int begin = 0;//用于存储查找的区间左端点值
        if(nums[left] == target) begin = left; 
        else return {-1, -1}; //不相等返回-1,-1即可

        right = nums.size() - 1;//更新right值，left值可以不用更新为0
        while(left < right)
        {
            int mid = left + (right - left + 1) / 2;
            if(nums[mid] > target) right = mid - 1;
            else left = mid;
        }
        int end = left;//用于存储查找区间的右端点值

        return {begin, end};
    }
};

3.浮点数二分

和前面的整数二分不同，浮点数不存在整数上下取整导致的边界问题，每次二分区间严格减半，因此，浮点数二分比整数二分简单得多，每次更新边界直接令 r = mid 或 l = mid即可。

790. 数的三次方根 - AcWing题库

浮点数二分除了更新区间和浮点数不同，还有一个细节就是二分终止条件，一般有两种写法，一种就是当前区间长度已经足够小。比如这题需要保留六位小数，我们可以在区间长度小于1e-8时结束循环，一般区间长度比保留位数还要小两个数量级。

#include<iostream>
using namespace std;

int main()
{
    double x;
    cin >> x;
    //数据的范围是-10000到10000,也可以写成-100到100
    double left = -10000, right = 10000;
    while(right - left > 1e-8)
    {
        double mid = (left + right) / 2;
        if(mid * mid * mid < x) left = mid;
        else right = mid;
    }
    printf("%.6lf",left);  
    return 0;
}

还有一种写法，就是直接把二分迭代100次，也就是把while(r - l > 1e-8)换成for(int i = 0; i < 100; ++i) 这句话的意思是把区间缩小2¹⁰⁰倍，由于2¹⁰⁰是个很大的数，所以这样也能让区间变得很小，也能得到我们的结果。

#include<iostream>
using namespace std;

int main()
{
    double x;
    cin >> x;
    
    double left = -10000, right = 10000;
    
    for(int i = 0;i < 100;i++)
    {
        double mid = (left + right) / 2;
        if(mid * mid * mid < x) left = mid;
        else right = mid;
    }
    printf("%.6lf",left);  
    return 0;
}