一、说明
您可以想象 MPC 具有系统的动态模型(线性时不变 (LTI) 系统中的矩阵 A)来模拟或预测模型未来的位置或行为。然后,控制器计算一系列控制输入,以最小化预定义的成本函数,同时考虑期望的目标和约束。
出于本文的目的,我用 C++ 准备了简单的模拟。目的是展示可以轻松复制以实现更高级模型动力学的原理。你可以在马库的GitHub上找到源代码。
二、模型预测控制( MPC )概述
2.1 基本概念
模型预测控制( MPC ) 是一种先进的过程控制方法,用于在满足一组约束的同时控制过程。自 20 世纪 80 年代以来,它一直在化工厂和炼油厂的流程工业中使用。近年来,它还被用于电力系统平衡模型[1]和电力电子领域。[2]模型预测控制器依赖于过程的动态模型,最常见的是通过系统辨识获得的线性经验模型。MPC 的主要优点是它允许优化当前时隙,同时考虑未来时隙。这是通过优化有限时间范围来实现的,但仅实现当前时隙,然后重复地再次优化,因此与线性二次调节器(LQR)不同。MPC 还能够预测未来事件并采取相应的控制措施。PID控制器不具备这种预测能力。尽管有研究通过专门设计的模拟电路来实现更快的响应时间,但 MPC 几乎普遍实现为数字控制。[3]
广义预测控制(GPC)和动态矩阵控制(DMC)是MPC的经典例子。
2.2 概述[编辑]
MPC 中使用的模型通常旨在表示复杂和简单动力系统的行为。MPC 控制算法的额外复杂性通常不需要为简单系统提供足够的控制,而简单系统通常可以通过通用PID 控制器很好地控制。PID 控制器难以实现的常见动态特性包括大时滞和高阶动态特性。
MPC 模型预测建模系统因变量的变化将由自变量的变化引起。在化学过程中,可由控制器调节的自变量通常是调节 PID 控制器的设定值(压力、流量、温度等)或最终控制元件(阀门、阻尼器等)。控制器无法调节的自变量被用作干扰。这些过程中的因变量是代表控制目标或过程约束的其他测量值。
MPC 使用当前工厂测量值、过程的当前动态状态、MPC 模型以及过程变量目标和限制来计算因变量的未来变化。计算这些变化是为了使因变量接近目标,同时遵守对自变量和因变量的约束。MPC 通常仅发出要实现的每个自变量的第一个变化,并在需要下一个变化时重复计算。
虽然许多实际过程不是线性的,但它们通常可以被认为在小操作范围内近似线性。大多数应用中都使用线性 MPC 方法,MPC 的反馈机制可以补偿由于模型和过程之间的结构不匹配而导致的预测误差。在仅由线性模型组成的模型预测控制器中,线性代数的叠加原理可以将多个自变量变化的影响相加,以预测因变量的响应。这将控制问题简化为一系列快速且稳健的直接矩阵代数计算。
当线性模型不足以准确地表示实际过程非线性时,可以使用多种方法。在某些情况下,可以在线性MPC模型之前和/或之后变换过程变量以减少非线性。该过程可以通过非线性 MPC 进行控制,该 MPC 直接在控制应用程序中使用非线性模型。非线性模型可以是经验数据拟合(例如人工神经网络)或基于基本质量和能量平衡的高保真动态模型的形式。非线性模型可以被线性化以导出卡尔曼滤波器或指定线性 MPC 的模型。
El-Gherwi、Budman 和 El Kamel 进行的一项算法研究表明,利用双模式方法可以显着减少在线计算,同时保持与未更改实现的比较性能。该算法基于控制器之间的信息交换并行解决 N 个凸优化问题。[5]
2.3 MPC背后的理论[编辑]
MPC 基于对象模型的迭代、有限范围优化。时t对当前工厂状态进行采样,并在未来相对较短的时间范围内计算成本最小化控制策略(通过数值最小化算法):![]() 。具体来说,使用在线或即时计算来探索从当前状态发出的状态轨迹,并找到(通过欧拉-拉格朗日方程的解)成本最小化控制策略,直到时间t+T。仅实施控制策略的第一步,然后再次对被控对象状态进行采样,并从新的当前状态开始重复计算,产生新的控制和新的预测状态路径。预测范围不断向前移动,因此 MPC 也称为后退范围控制。虽然这种方法不是最优的,但在实践中却给出了非常好的结果。为了寻找欧拉-拉格朗日型方程的快速求解方法、了解 MPC 局部优化的全局稳定性特性以及总体上改进 MPC 方法,已经进行了大量的学术研究。
。具体来说,使用在线或即时计算来探索从当前状态发出的状态轨迹,并找到(通过欧拉-拉格朗日方程的解)成本最小化控制策略,直到时间t+T。仅实施控制策略的第一步,然后再次对被控对象状态进行采样,并从新的当前状态开始重复计算,产生新的控制和新的预测状态路径。预测范围不断向前移动,因此 MPC 也称为后退范围控制。虽然这种方法不是最优的,但在实践中却给出了非常好的结果。为了寻找欧拉-拉格朗日型方程的快速求解方法、了解 MPC 局部优化的全局稳定性特性以及总体上改进 MPC 方法,已经进行了大量的学术研究。
2.4 MPC原理[编辑]
模型预测控制是一种多变量控制算法,它使用:
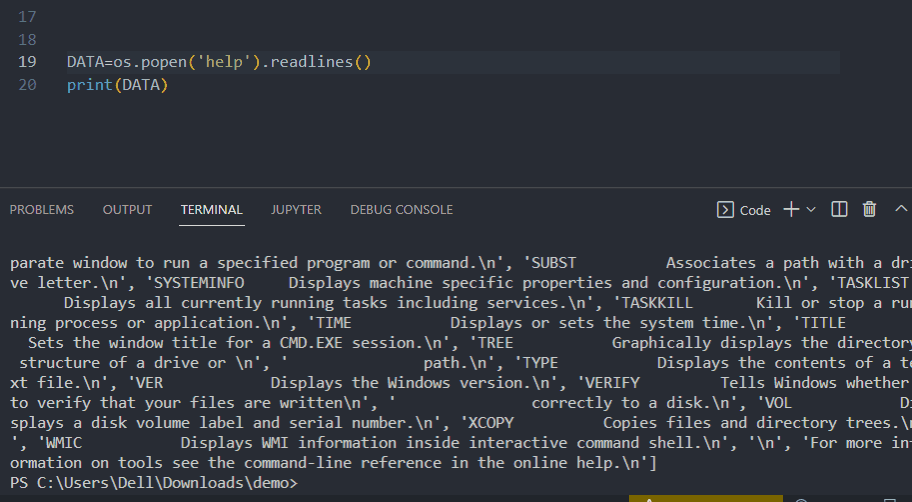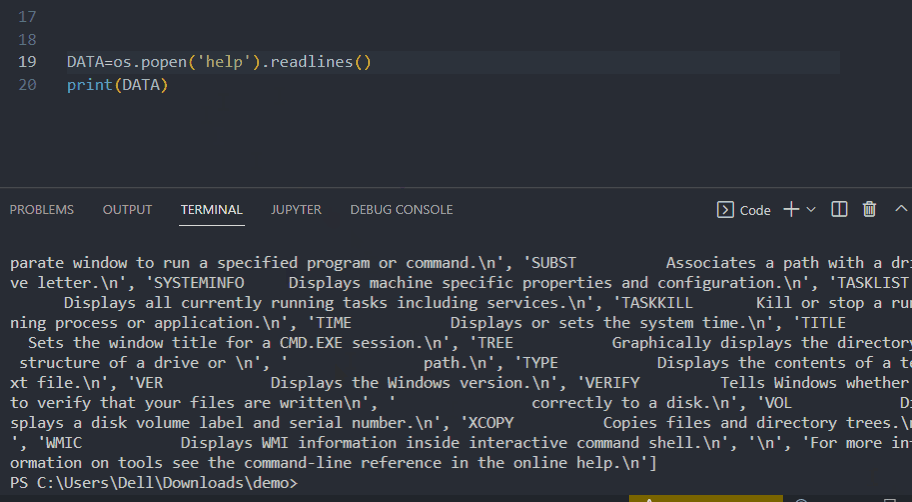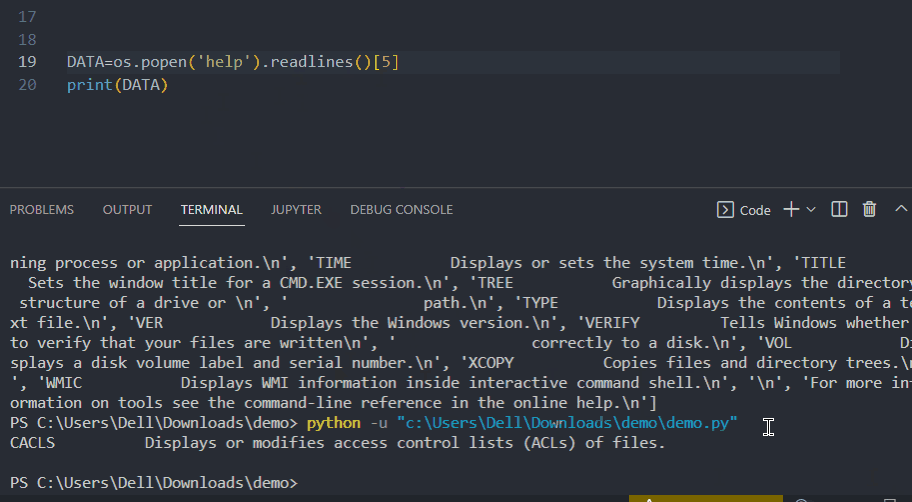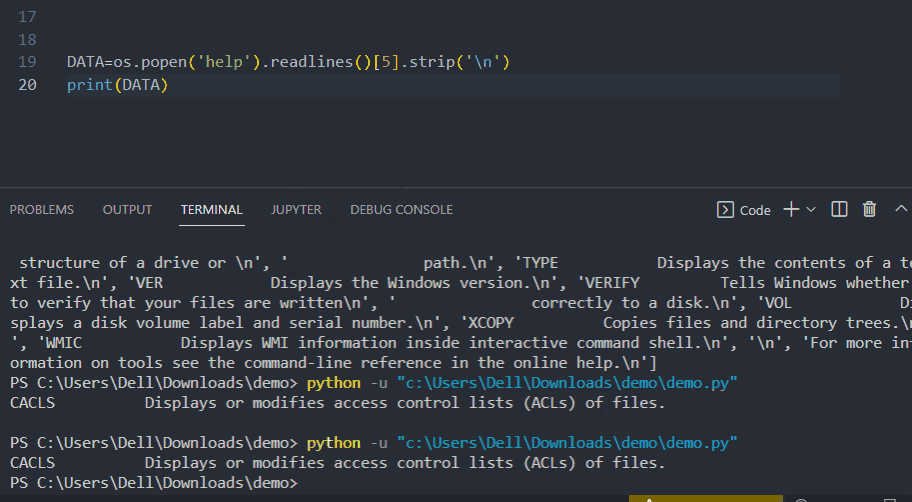
- 过程的内部动态模型
- 后退范围内的成本函数J
- 使用控制输入u最小化成本函数J 的优化算法
用于优化的二次成本函数的示例如下:
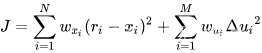
不违反限制(低/高限制)

三、MPC的C++应用库
我在 C++ 中精确应用的标准模型预测控制 (MPC) 公式可以定义如下,
考虑具有以下状态空间表示的离散时间线性系统:
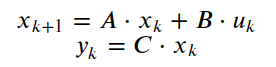
在这里,
- xk是时间步k的状态向量,
- uk是时间步k的控制输入向量,
- yk是时间步k的输出向量,
- A是状态转移矩阵(模型动力学),
- B是控制输入矩阵,
- C是输出矩阵。
模型预测控制 (MPC) 的目标是在满足系统约束的同时,最小化有限预测范围N上的成本函数。成本函数通常包括二次项,惩罚与参考轨迹和控制输入的偏差:
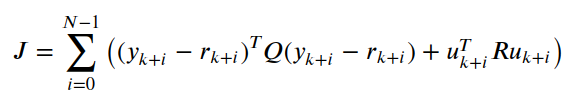
在这里,
- N是预测范围,
- Q是输出权重矩阵,
- R是控制输入权重矩阵,
- rk + i是时间步k + i处的参考轨迹。
MPC 问题被表述为一个优化问题,
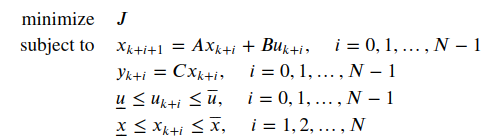
这里,控制输入 u 和状态 x 位于下限和上限之下。
该公式概述了我在 C++ 模拟中应用的线性离散时间系统的标准模型预测控制的数学结构。
在实践中(检查源代码),我们在每个时间步解决这个优化问题,以计算预测范围内的最优控制输入,然后将第一个控制输入应用于系统。
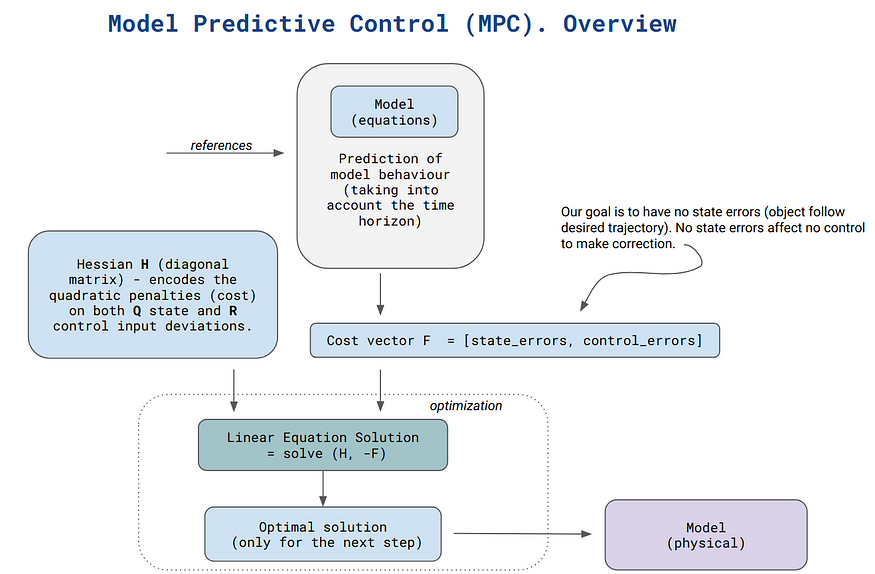
MPC 概述(按作者)
我们可以分解源代码并显示算法的关键特征,
- Hessian 矩阵(H):一般来说,Hessian 矩阵是一个与二阶导数相关的数学概念,提供有关多元函数曲率的信息。
在优化的情况下,我们使用 Hassian 来分析目标函数在临界点(最小值或最大值)附近的行为。在我们的特定情况下,Hessian 矩阵对状态和控制输入偏差的二次惩罚进行编码。 - 成本向量 (F):该向量是与所需参考状态的预测状态偏差和控制输入偏差的零值的组合。该向量表示成本函数的线性项,并指导优化过程以最小化成本。
- 优化过程:优化过程旨在找到使成本函数最小化的控制输入的变化。在二次优化问题的背景下,这是通过求解由优化问题的最优性条件产生的一组线性方程来实现的。
我们求解由最优性条件形成的线性方程。此操作计算应应用于当前控制输入的控制输入的最佳变化,以便使系统状态更接近所需的参考,同时最小化成本。
下面我提供了您可以在计算机上运行的模拟的输出。
下面的第一个模拟提供了有关 MPC 如何执行以接近所需恒定位置(值)的信息。
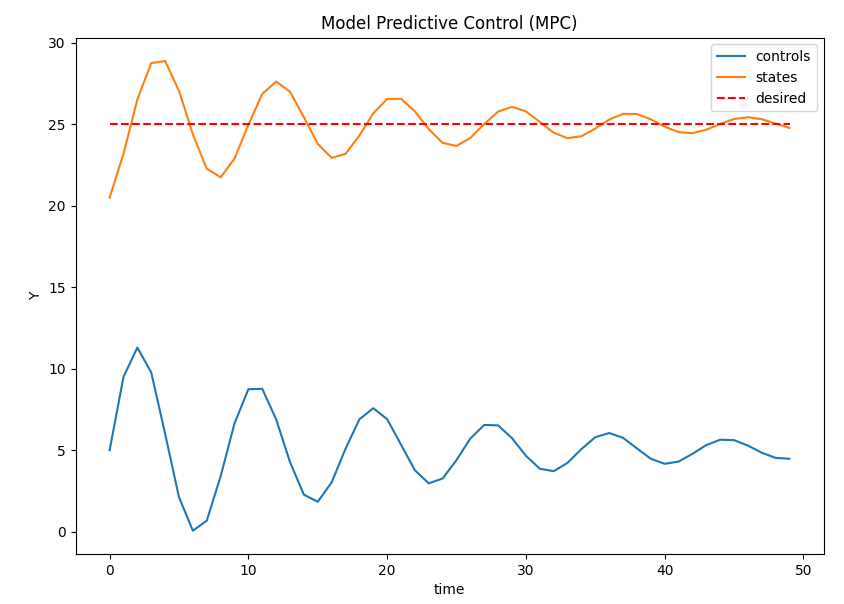
MPC 性能。模拟1
您可以运行的第二个模拟提供 MPC 性能输出,而所需的轨迹具有正弦函数的形状。成本函数(矩阵值 Q、R)的正确选择会影响状态以及系统如何随时间稳定。
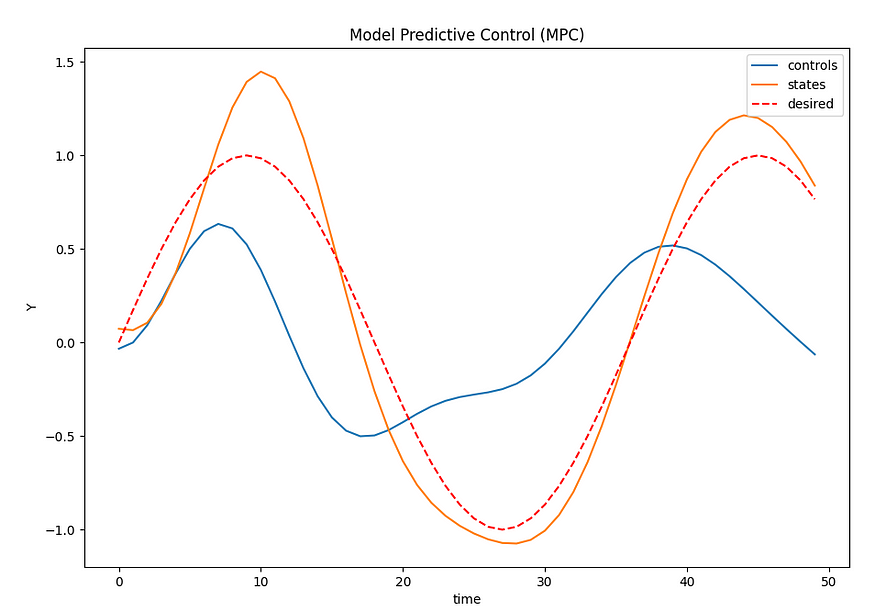
MPC 性能。模拟2
四、后记
关于控制论的MPC,本文只是管中窥豹,并不能大量展开;有关详细理论尚需要广泛阅读更加专业的书籍,本篇只是打开了一面窗户,让人工智能工程师根据实际需要做出自我选择,是否要在控制论走的更远一些?感谢您的阅读。
参考资料:
马库斯·布赫霍尔茨