本篇文章来简单介绍一下Linux操作系统中权限的基本概念和一些操作方法，对Linux权限有一个基本的了解，希望对大家学习Linux有所帮助。

目录

1.权限的概念

2.Linux权限管理

2.1 文件访问者的分类

2.2 文件类型与访问权限（事物属性）

2.3 文件权限值的表示方法

2.4.文件访问权限的相关设置方法

3.目录的权限

---

1.权限的概念

Linux下有两种用户：超级用户（root）、普通用户。

• 超级用户：可以在linux系统下做任何事情，不受限制
• 普通用户：在linux下做有限的事情。
• 超级用户的命令提示符是“#”，普通用户的命令提示符是“$”。

命令：su [用户名]

功能：切换用户。

例如，要从root用户切换到普通用户user，则使用 su user。 要从普通用户user切换到root用户则使用 su root（root可以省略），此时系统会提示输入root用户的口令（密码）。

2.Linux权限管理

2.1 文件访问者的分类

• 文件和文件目录的所有者：u---User（中国平民 法律问题）
• 文件和文件目录的所有者所在的组的用户：g---Group（不多说）
• 其它用户：o---Others （外国人）

2.2 文件类型与访问权限（事物属性）

示例：

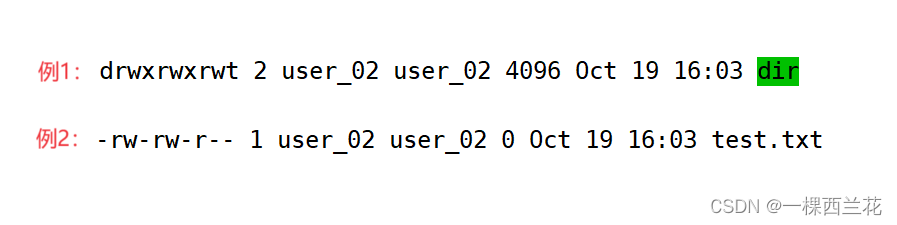
 文件类型

• d：文件夹，示例1就是文件夹
• -：普通文件，示例2就是普通文件
• l：软链接（类似Windows的快捷方式）
• b：块设备文件（例如硬盘、光驱等）
• p：管道文件
• c：字符设备文件（例如屏幕等串口设备）
• s：套接口文件

基本指令

• 'r' 读：Read对文件而言，具有读取文件内容的权限；对目录来说，具有浏览该目录信息的权限
• 'w' 写：Write对文件而言，具有修改文件内容的权限；对目录来说，具有删除移动目录内文件的权限
• 'x' 执行：execute对文件而言，具有执行文件的权限；对目录来说，具有进入目录的权限
• '-' 表示不具有该项权限

2.3 文件权限值的表示方法

1.字符表示方法

Linux表示	说明	Linux表示	说明
r--	只读	-w-	仅可写
--x	仅可执行	rw-	可读可写
-wx	可写可执行	r-x	可读可执行
rwx	可读可写可执行	---	无权限

2.八进制数值表示法

权限符号（读写执行）	八进制	二进制
r--	4	100
-w-	2	010
--x	1	001
rw-	6	110
rx	5	101
wx	3	011
rwx	7	111
---	0	000

2.4.文件访问权限的相关设置方法

a)chmod

功能：设置文件的访问权限

格式：chmod [参数] 权限 文件名

常用选项：

R -> 递归修改目录文件的权限

说明：只有文件的拥有者和root才可以改变文件的权限

chmod 命令权限值的格式

1.用户表示符+ - =权限字符

• +：向权限范围增加权限代号所表示的权限
• - ：向权限范围取消权限代号所表示的权限
• =：向权限范围赋予权限代号所表示的权限

用户符号：

• u：拥有者
• g：拥有者同组用
• o：其它用户
• a：所有用户

实例：

chmod u+w /home/abc.txt   //拥有者增加写权限
chmod o-x /home/abc.txt    //其他用户取消执行权限

chmod a=x /home/abc.txt   //所有用户只有执行权限

2. 三位8进制数字

chmod 664 /home/abc.txt   //拥有者读和写  所属组读和写  其他用户只读
chmod 640 /home/abc.txt   //拥有者读和写  所属组只读    其他用户没有权限

实例：

b)chown

功能：修改文件的拥有者

格式：chown [参数] 用户名 文件名

实例：

# chown user1 f1  将f1文件的拥有者改为user1

c)chgrp

功能：修改文件或目录的所属组

格式：chgrp [参数] 用户组名 文件名

常用选项：-R 递归修改文件或目录的所属组

实例：

chgrp users test.txt

d)umask

功能：

查看或修改文件掩码
新建文件夹默认权限=0666（0开头表示八进制），新建目录默认权限=0777
但实际上你所创建的文件和目录，看到的权限往往不是上面这个值。原因就是创建文件或目录的时候还要受到umask的影响。假设默认权限是mask，则实际创建的出来的文件权限是: mask & (~umask)

格式：umask 权限值

说明：超级用户默认掩码umask值为0022，普通用户默认为0002。

实例：

# umask 755
# umask //查看
# umask 044//设置

3.目录的权限

• 可执行权限: 如果目录没有可执行权限, 则无法cd到目录中
• 可读权限: 如果目录没有可读权限, 则无法用ls等命令查看目录中的文件内容
• 可写权限: 如果目录没有可写权限, 则无法在目录中创建文件, 也无法在目录中删除文件

于是, 问题来了~~

换句话来讲, 就是只要用户具有目录的写权限, 用户就可以删除目录中的文件, 而不论这个用户是否有这个文件的写权限。文件能不能被删除要看目录的权限，跟文件本身的权限无关。

这好像不太科学啊, 张三和李四在同一目录下操作，张三创建的一个文件, 凭什么被李四可以删掉?

为了解决这个不科学的问题, Linux引入了粘滞位的概念。

粘滞位

当一个目录被设置为"粘滞位"(用chmod +t 目录),则该目录下的文件只能由

1. 超级管理员删除
2. 该目录的所有者删除，一般也为root
3. 该文件的所有者删除

关于权限的总结

• 目录的可执行权限是表示你可否在目录下执行命令。
• 如果目录没有-x权限，则无法对目录执行任何命令，甚至无法cd 进入目录, 即使目录仍然有-r 读权限（这个地方很容易犯错，认为有读权限就可以进入目录读取目录下的文件）
• 而如果目录具有-x权限，但没有-r权限，则用户可以执行命令，可以cd进入目录。但由于没有目录的读权限，所以在目录下，即使可以执行ls命令，但仍然没有权限读出目录下的文档

本篇结束！