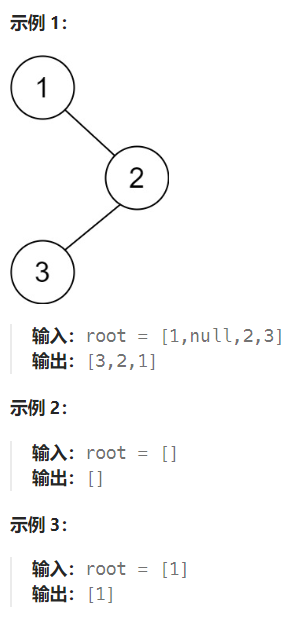
题目链接

Python3

方法一： 递归 $⟮O(n)⟯$

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        """后序遍历 [ 左子树 右子树 根结点 ] 递归 """
        def postorder(node):
            if not node:
                return 
            postorder(node.left) # 左子树 
            postorder(node.right) # 右子树
            ans.append(node.val)  # 根结点

        ans = []
        postorder(root)
        return ans

方法二： 迭代 $⟮O(n)⟯$

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        """后序遍历 [左子树  右子树  根]  迭代"""

        ans = []
        stack = []
        cur = root
        pre = None
        while cur or stack:
            while cur:
                stack.append(cur)
                cur = cur.left # 左

            cur = stack.pop()
            if not cur.right or cur.right == pre: ## 右边 已遍历完
                ans.append(cur.val) # 根 
                pre = cur 
                cur = None 
            else:
                stack.append(cur)
                cur = cur.right  # 右
        return ans

方法三： Morris $⟮O(n)、O(1)⟯$

写法一

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        """ 后序遍历 [ 左子树 右子树 根 ]  Morris  O(N) O(1)"""
        ### 写法一  根 右 左   反转结果列表  
        # 根据 前序遍历 修改
        ans = []
        cur, pre = root, None 
        while cur:
            if not cur.right:
                ans.append(cur.val)  ##
                cur = cur.left

            # 有右孩子
            else:
                # 找 pre 
                pre = cur.right 
                while pre.left and pre.left != cur:
                    pre = pre.left  
                if not pre.left: ## 找到 mostleft
                    pre.left = cur
                    ans.append(cur.val)  ## 
                    cur = cur.right
                else:
                    pre.left = None 
                    cur = cur.left
        return ans[::-1]

写法二

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        """ 后序遍历 [ 左子树 右子树 根 ]  Morris  O(N) O(1)"""
        ## 需要 增加 一个 反转模块
        def addPath(node: TreeNode):
            count = 0
            while node:
                count += 1
                ans.append(node.val)
                node = node.right
            i, j = len(ans) - count, len(ans) - 1
            while i < j:
                ans[i], ans[j] = ans[j], ans[i]
                i += 1
                j -= 1
        ### 
        ans = []
        cur, pre = root, None 
        while cur:
            if not cur.left:
                cur = cur.right 

            # 有左孩子
            else:
                # 找 pre 
                pre = cur.left 
                while pre.right and pre.right != cur:
                    pre = pre.right  
                if not pre.right:
                    pre.right = cur
                    cur = cur.left 
                else:
                    pre.right = None 
                    addPath(cur.left) ## 
                    cur = cur.right 
        addPath(root)  ## 
        return ans 

C++

方法一： 递归 $⟮O(n)⟯$

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 子模块
    void postorder(TreeNode* node, vector<int> &ans){
        if (node == nullptr){
            return;
        }
        postorder(node->left, ans);
        postorder(node->right, ans);
        ans.emplace_back(node->val);
    }

    // 主模块
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> ans;
        postorder(root, ans);
        return ans;
    }
};

方法二： 迭代 $⟮O(n)⟯$

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> ans;
        stack<TreeNode*>stk;
        TreeNode* cur = root;
        TreeNode* pre = nullptr;

        while (cur != nullptr || !stk.empty()){
            while (cur != nullptr){
                stk.emplace(cur);
                cur = cur->left;
            }

            cur = stk.top();
            stk.pop();
            if (cur->right == nullptr || cur->right == pre){// 右子树 遍历完，处理根结点
                ans.emplace_back(cur->val);
                pre = cur;
                cur = nullptr;
            }
            else{// 右子树
                stk.emplace(cur);
                cur = cur->right;
            }
        }
        return ans;
    }
};

方法三： Morris $⟮O(n)、O(1)⟯$

写法一

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> ans;
        TreeNode* cur = root;
        TreeNode* pre = nullptr;

        while (cur != nullptr){
            if (cur->right == nullptr){
                ans.emplace_back(cur->val);
                cur = cur->left;
            }
            else{
                // 找 pre 
                pre = cur->right;
                while (pre->left != nullptr && pre->left != cur){
                    pre = pre->left;
                }
                if (pre->left == nullptr){
                    pre->left = cur;
                    ans.emplace_back(cur->val);
                    cur = cur->right;
                }
                else{
                    pre->left = nullptr;
                    cur = cur->left;
                }
            }
        }

        reverse(ans.begin(), ans.end()); // 该函数为 void ,不能直接返回
        return ans;
    }
};

写法二

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // 子模块
    void addPath(TreeNode* node, vector<int> &ans){
        int count = 0;
        while (node != nullptr){
            count += 1;
            ans.emplace_back(node->val);
            node = node->right;
        }

        int i = ans.size() - count, j = ans.size() - 1;
        while (i < j){
            swap(ans[i], ans[j]);
            i += 1;
            j -= 1;
        }

    }

    // 主模块
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> ans;
        TreeNode* cur = root;
        TreeNode* pre = nullptr;

        while (cur != nullptr){
            if (cur->left == nullptr){
                cur = cur->right;
            }
            else{
                //找 pre 
                pre = cur->left;
                while (pre->right != nullptr && pre->right != cur){
                    pre = pre->right;
                }
                if (pre->right == nullptr){
                    pre->right = cur;
                    cur = cur->left;
                }
                else{
                    pre->right  = nullptr;
                    addPath(cur->left, ans);
                    cur = cur->right;
                }
            }

        }
        addPath(root, ans);
        return ans;
    }
};