自然语言处理---RNN、LSTM、GRU模型

RNN模型

RNN模型概述

RNN(Recurrent Neural Network)，中文称作循环神经网络，它一般以序列数据为输入，通过网络内部的结构设计有效捕捉序列之间的关系特征，一般也是以序列形式进行输出。
RNN的循环机制使模型隐层上一时间步产生的结果，能够作为当下时间步输入的一部分(当下时间步的输入除了正常的输入外还包括上一步的隐层输出)对当下时间步的输出产生影响。

RNN模型的作用

因为RNN结构能够很好利用序列之间的关系，因此针对自然界具有连续性的输入序列，如人类的语言，语音等进行很好的处理，广泛应用于NLP领域的各项任务，如文本分类，情感分析，意图识别，机器翻译等。
以一个用户意图识别的例子对RNN的运行过程进行简单的分析：
- 第一步：用户输入了"What time is it ?"，首先需要对它进行基本的分词，因为RNN是按照顺序工作的，每次只接收一个单词进行处理。
- 第二步：首先将单词"What"输送给RNN，它将产生一个输出O1。
- 第三步：继续将单词"time"输送给RNN，但此时RNN不仅仅利用"time"来产生输出O2，还会使用来自上一层隐层输出O1作为输入信息。
- 第四步：重复这样的步骤，直到处理完所有的单词。
- 第五步：最后将最终的隐层输出O5进行处理来解析用户意图。

RNN模型的分类

从两个角度对RNN模型进行分类，第一个角度是输入和输出的结构，第二个角度是RNN的内部构造。
按照输入和输出的结构进行分类：
- N vs N - RNN
- N vs 1 - RNN
- 1 vs N - RNN
- N vs M - RNN
按照RNN的内部构造进行分类:
- 传统RNN
- LSTM
- Bi-LSTM
- GRU
- Bi-GRU

N vs N - RNN
它是RNN最基础的结构形式，最大的特点就是：输入和输出序列是等长的。由于这个限制的存在，使其适用范围比较小，可用于生成等长度的合辙诗句。
N vs 1 - RNN
有时要处理的问题输入是一个序列，而要求输出是一个单独的值而不是序列，应该怎样建模呢？只要在最后一个隐层输出h上进行线性变换就可以了，大部分情况下，为了更好的明确结果，还要使用sigmoid或者softmax进行处理。这种结构经常被应用在文本分类问题上。
1 vs N - RNN
如果输入不是序列而输出为序列的情况怎么处理呢？最常采用的一种方式就是使该输入作用于每次的输出之上。这种结构可用于将图片生成文字任务等。
N vs M - RNN
这是一种不限输入输出长度的RNN结构，它由编码器和解码器两部分组成，两者的内部结构都是某类RNN，它也被称为seq2seq架构。输入数据首先通过编码器，最终输出一个隐含变量c，之后最常用的做法是使用这个隐含变量c作用在解码器进行解码的每一步上，以保证输入信息被有效利用。

seq2seq架构最早被提出应用于机器翻译，因为其输入输出不受限制，如今也是应用最广的RNN模型结构。在机器翻译，阅读理解，文本摘要等众多领域都进行了非常多的应用实践。

传统RNN模型

RNN结构分析

结构解释图

内部结构分析

在中间的方块部分，它的输入有两部分，分别是h(t-1)以及x(t)，代表上一时间步的隐层输出，以及此时间步的输入，它们进入RNN结构体后，会"融合"到一起，这种融合根据结构解释可知，是将二者进行拼接，形成新的张量[x(t), h(t-1)]，之后这个新的张量将通过一个全连接层(线性层)，该层使用tanh作为激活函数，最终得到该时间步的输出h(t)，它将作为下一个时间步的输入和x(t+1)一起进入结构体。以此类推。

根据结构分析得出内部计算公式：

激活函数tanh的作用：用于帮助调节流经网络的值，tanh函数将值压缩在-1和1之间。

传统RNN优缺点

传统RNN的优势

由于内部结构简单，对计算资源要求低，相比RNN变体：LSTM和GRU模型参数总量少了很多，在短序列任务上性能和效果都表现优异。

传统RNN的缺点

传统RNN在解决长序列之间的关联时，通过实践，证明经典RNN表现很差，原因是在进行反向传播的时候，过长的序列导致梯度的计算异常，发生梯度消失或爆炸。

梯度消失或爆炸介绍

根据反向传播算法和链式法则，梯度的计算可以简化为以下公式

其中sigmoid的导数值域是固定的，在[0, 0.25]之间，而一旦公式中的w也小于1，那么通过这样的公式连乘后，最终的梯度就会变得非常非常小，这种现象称作梯度消失。反之，如果人为的增大w的值，使其大于1，那么连乘够就可能造成梯度过大，称作梯度爆炸。
梯度消失或爆炸的危害:
- 如果在训练过程中发生了梯度消失，权重无法被更新，最终导致训练失败；梯度爆炸所带来的梯度过大，大幅度更新网络参数，在极端情况下，结果会溢出（NaN值）。

LSTM模型

LSTM（Long Short-Term Memory）也称长短时记忆结构，它是传统RNN的变体，与经典RNN相比能够有效捕捉长序列之间的语义关联，缓解梯度消失或爆炸现象。同时LSTM的结构更复杂，它的核心结构可以分为四个部分去解析：遗忘门、输入门、细胞状态、输出门。

LSTM结构分析

遗忘门

遗忘门部分结构图与计算公式

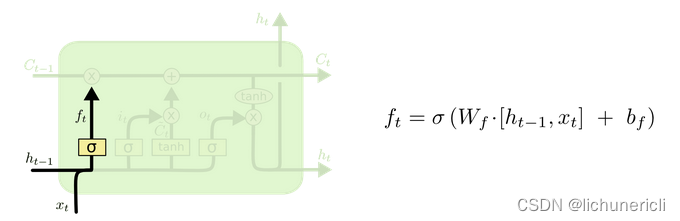
遗忘门结构分析
- 与传统RNN的内部结构计算非常相似，首先将当前时间步输入x(t)与上一个时间步隐含状态h(t-1)拼接，得到[x(t), h(t-1)]，然后通过一个全连接层做变换，最后通过sigmoid函数进行激活得到f(t)。
- 可以将f(t)看作是门值，好比一扇门开合的大小程度，门值都将作用在通过该扇门的张量，遗忘门门值将作用的上一层的细胞状态上，代表遗忘过去的多少信息，又因为遗忘门门值是由x(t)，h(t-1)计算得来的，因此整个公式意味着根据当前时间步输入和上一个时间步隐含状态h(t-1)来决定遗忘多少上一层的细胞状态所携带的过往信息。

激活函数sigmiod的作用：用于帮助调节流经网络的值，sigmoid函数将值压缩在0和1之间。

输入门

输入门部分结构图与计算公式

输入门结构分析
- 输入门的计算公式有两个，第一个就是产生输入门门值的公式，它和遗忘门公式几乎相同，区别只是在于它们之后要作用的目标上。这个公式意味着输入信息有多少需要进行过滤。输入门的第二个公式是与传统RNN的内部结构计算相同。对于LSTM来讲，它得到的是当前的细胞状态，而不是像经典RNN一样得到的是隐含状态。

细胞状态

细胞状态更新图与计算公式

细胞状态更新分析
- 细胞更新的结构与计算公式非常容易理解，这里没有全连接层，只是将刚刚得到的遗忘门门值与上一个时间步得到的C(t-1)相乘，再加上输入门门值与当前时间步得到的未更新C(t)相乘的结果。最终得到更新后的C(t)作为下一个时间步输入的一部分。整个细胞状态更新过程就是对遗忘门和输入门的应用。

输出门

输出门部分结构图与计算公式

输出门结构分析
- 输出门部分的公式也是两个，第一个即是计算输出门的门值，它和遗忘门，输入门计算方式相同。第二个即是使用这个门值产生隐含状态h(t)，他将作用在更新后的细胞状态C(t)上，并做tanh激活，最终得到h(t)作为下一时间步输入的一部分。整个输出门的过程，就是为了产生隐含状态h(t)。

Bi-LSTM

Bi-LSTM概述

Bi-LSTM即双向LSTM，它没有改变LSTM本身任何的内部结构，只是将LSTM应用两次且方向不同，再将两次得到的LSTM结果进行拼接作为最终输出。

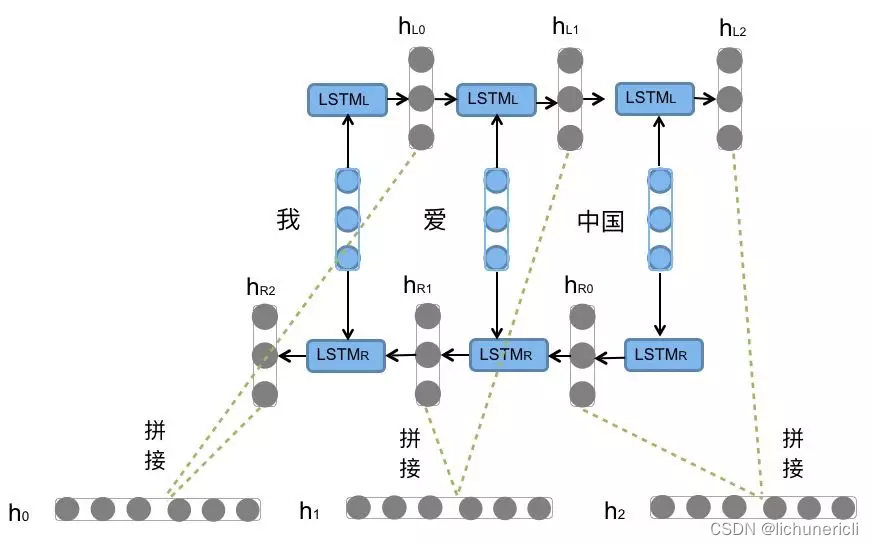
Bi-LSTM结构分析

图中对"我爱中国"这句话或者叫这个输入序列，进行了从左到右和从右到左两次LSTM处理，将得到的结果张量进行了拼接作为最终输出。这种结构能够捕捉语言语法中一些特定的前置或后置特征，增强语义关联，但是模型参数和计算复杂度也随之增加了一倍，一般需要对语料和计算资源进行评估后决定是否使用该结构

GRU模型

GRU（Gated Recurrent Unit）也称门控循环单元结构，它也是传统RNN的变体，同LSTM一样能够有效捕捉长序列之间的语义关联，缓解梯度消失或爆炸现象。同时它的结构和计算要比LSTM更简单，它的核心结构可以分为两个部分去解析：更新门、重置门。

GRU结构分析

结构解释图

GRU的更新门和重置门结构图

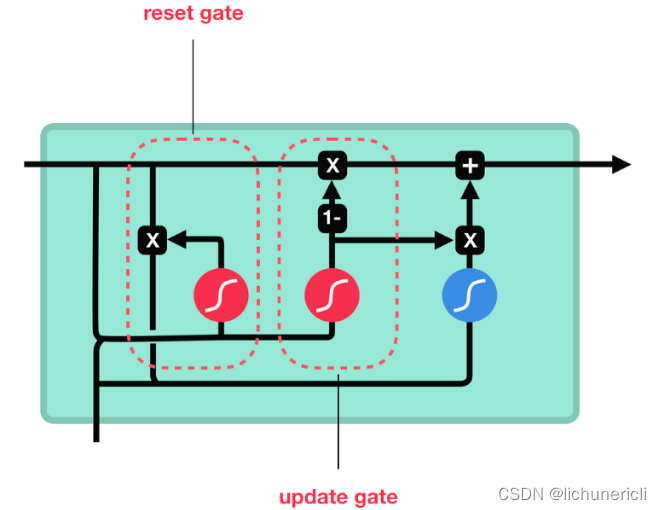
内部结构分析

和之前分析过的LSTM中的门控一样，首先计算更新门和重置门的门值，分别是z(t)和r(t)，计算方法就是使用X(t)与h(t-1)拼接进行线性变换，再经过sigmoid激活。之后重置门门值作用在了h(t-1)上，代表控制上一时间步传来的信息有多少可以被利用。
接着就是使用这个重置后的h(t-1)进行基本的RNN计算，即与x(t)拼接进行线性变化，经过tanh激活，得到新的h(t)。
最后更新门的门值会作用在新的h(t)，而1-门值会作用在h(t-1)上，随后将两者的结果相加，得到最终的隐含状态输出h(t)，这个过程意味着更新门有能力保留之前的结果，当门值趋于1时，输出就是新的h(t)，而当门值趋于0时，输出就是上一时间步的h(t-1)。

Bi-GRU

Bi-GRU与Bi-LSTM的逻辑相同，都是不改变其内部结构，而是将模型应用两次且方向不同，再将两次得到的LSTM结果进行拼接作为最终输出。

GRU优缺点

GRU的优势
- GRU和LSTM作用相同，在捕捉长序列语义关联时，能有效抑制梯度消失或爆炸，效果都优于传统RNN且计算复杂度相比LSTM要小。
GRU的缺点:
- GRU仍然不能完全解决梯度消失问题，同时其作用RNN的变体，有着RNN结构本身的一大弊端，即不可并行计算，这在数据量和模型体量逐步增大的未来，是RNN发展的关键瓶颈。