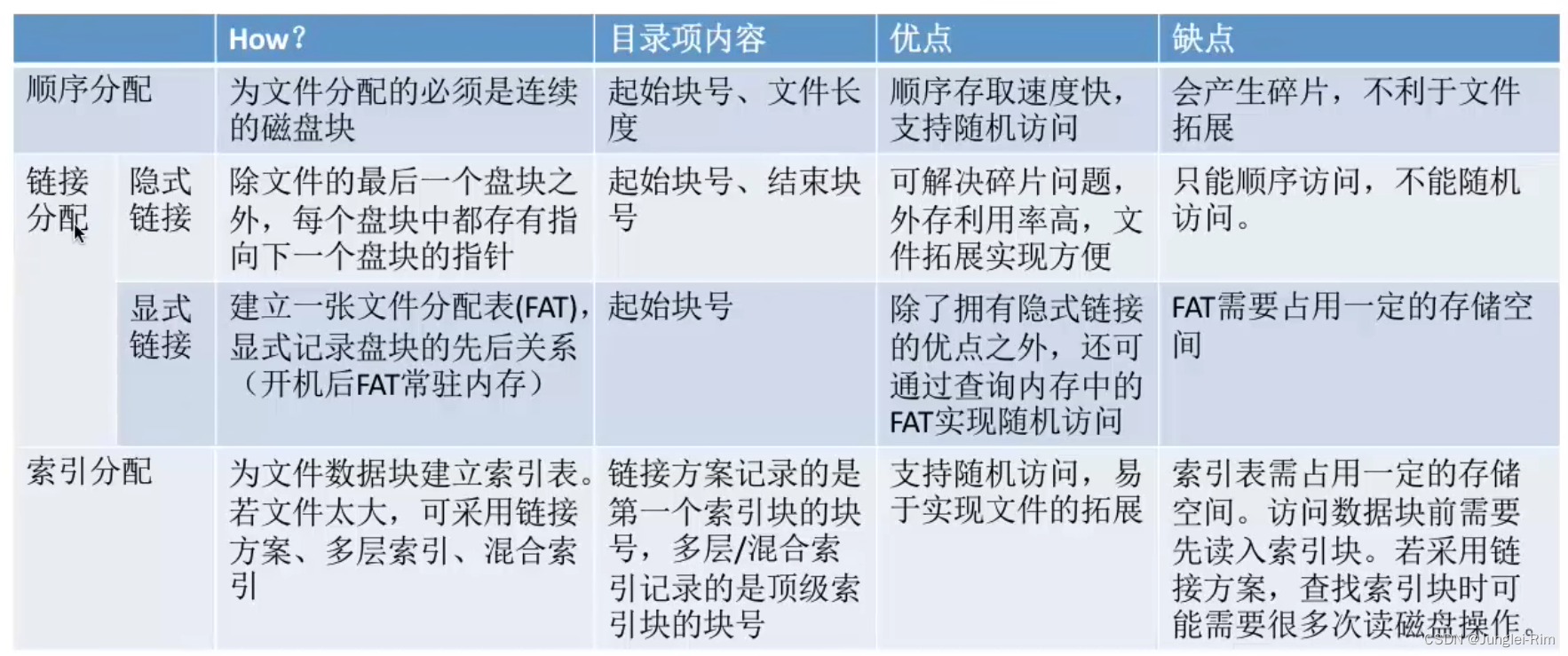
如图5-4所示，有n（n≤100）个建筑物。左侧是俯视图（左上角为建筑物编号，右下角为高度），右侧是从南向北看的正视图。

输入每个建筑物左下角坐标（即x、y坐标的最小值）、宽度（即x方向的长度）、深度（即y方向的长度）和高度（以上数据均为实数），输出正视图中能看到的所有建筑物，按照左下角x坐标从小到大进行排序。左下角x坐标相同时，按y坐标从小到大排序。输入保证不同的x坐标不会很接近（即任意两个x坐标要么完全相同，要么差别足够大，不会引起精度问题）。
【分析】
注意到建筑物的可见性等价于南墙的可见性，可以在输入之后直接忽略“深度”这个参数。
把所有建筑物按照左下角坐标排序，然后依次判断可见性。
判断可见性看上去比较麻烦，因为一个建筑物可能只有部分可见，无法枚举所有x坐标，因为x坐标是实数，所以有无穷多个。
解决方法是离散化，即把无穷变为有限。就是把每一个建筑物的两端的坐标x和x+w放进一个数组里，然后排序并去重，做完这些操作就相当于分割了如下的若干个区间。

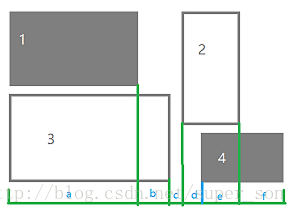
区间具有如下性质:
1.该区间要么不存在建筑物，要么存在若干个建筑物。
2.在区间中的建筑物，一定会把区间给填满，不会出现建筑物只占区间部分空间的情况。
所以我们只需要对每个建筑物，检查每个区间，判断它是否在该区间中。根据区间性质，只需在这个区间里任选一个点（例如中点），就能判断出一个建筑物是否在整个区间内。如果建筑物在该区间中，那么再检查它前面是否有一个比它更高的在该区间的建筑物。

样例：
输入

14
160 0 30 60 30
125 0 32 28 60
95 0 27 28 40
70 35 19 55 90
0 0 60 35 80
0 40 29 20 60
35 40 25 45 80
0 67 25 20 50
0 92 90 20 80
95 38 55 12 50
95 60 60 13 30
95 80 45 25 50
165 65 15 15 25
165 85 10 15 35

输出

5
9
4
3
10
2
1
14

解法：

use std::io;
#[derive(Debug, Clone, Copy)]
struct Building {
    pos: (f64, f64),
    w: f64,
    d: f64,
    h: f64,
    id: usize,
}
fn main() {
    let mut buf = String::new();
    io::stdin().read_line(&mut buf).unwrap();
    let n: usize = buf.trim().parse().unwrap();
    let mut buildings: Vec<Building> = vec![];
    let mut xpoint: Vec<f64> = vec![];
    for i in 0..n {
        let mut buf = String::new();
        io::stdin().read_line(&mut buf).unwrap();
        let v: Vec<f64> = buf.split_whitespace().map(|e| e.parse().unwrap()).collect();
        let b = Building {
            pos: (v[0], v[1]),
            w: v[2],
            d: v[3],
            h: v[4],
            id: i + 1,
        };
        buildings.push(b);
        xpoint.push(b.pos.0);
        xpoint.push(b.pos.0 + b.w);
    }
    //println!("{:?}", buildings);
    buildings.sort_by(|a, b| a.pos.partial_cmp(&b.pos).unwrap());
    xpoint.sort_by(|a, b| a.partial_cmp(b).unwrap());
    xpoint.dedup();
    //println!("{:?}", buildings);
    //println!("{:?}", xpoint);
    for i in 0..n {
        let mut bvis = false;
        for j in 0..xpoint.len() - 1 {
            if is_visible(&buildings, i, (xpoint[j], xpoint[j + 1])) {
                bvis = true;
                break;
            }
        }
        if bvis {
            println!("{}", buildings[i].id);
        }
    }
}

fn is_visible(buildings: &Vec<Building>, i: usize, interval: (f64, f64)) -> bool {
    if !is_in_interval(buildings, i, interval) {
        return false;
    }
    for k in 0..buildings.len() {
        if buildings[i].pos.1 > buildings[k].pos.1
            && buildings[i].h <= buildings[k].h
            && is_in_interval(buildings, k, interval)
        {
            return false;
        }
    }
    return true;
}
fn is_in_interval(buildings: &Vec<Building>, i: usize, interval: (f64, f64)) -> bool {
    let mid = (interval.0 + interval.1) / 2.0;
    return mid >= buildings[i].pos.0 && mid <= buildings[i].pos.0 + buildings[i].w;
}