【TensorFlow1.X】系列学习笔记【入门二】

大量经典论文的算法均采用 TF 1.x 实现, 为了阅读方便, 同时加深对实现细节的理解, 需要 TF 1.x 的知识

---

---

前言

学习了张量、计算图、会话等基础知识，下一步就是实现神经网络的搭建了，本篇博文将讲解搭建神经网络的过程，并简练总结搭建八股。【参考】

---

神经网络的参数

神经网络的参数是指在神经网络模型中需要学习的可调整值。这些参数用于调整模型的行为，定了神经网络的行为和性能，使其能够更好地拟合训练数据和进行预测。
在典型的神经网络中，参数主要存在于两个部分，用变量表示：

1. 权重(Weights)：
   权重是连接神经网络中不同层的神经元之间的参数。每个连接都有一个关联的权重，用于调整信息在网络中的传递。权重决定了每个输入对于特定神经元的重要性。在训练过程中，神经网络通过优化算法来调整权重，以最小化预测输出与实际输出之间的差距。
2. 偏置(Biases)：
   偏置是神经元的可调整参数，用于调整神经元的激活阈值。每个神经元都有一个关联的偏置值，它在计算神经元的输出时被加到加权输入上。偏置允许神经元对不同的输入模式做出不同的响应。

这些权重和偏置参数是在训练过程中学习的，通过反向传播算法和优化方法(如梯度下降)来更新,训练过程旨在最小化损失函数，以使神经网络能够更准确地进行预测。

在 TensorFlow 1.x 中，可以使用以下方法来初始化神经网络的参数：

方法	功能
tf.random_normal()	生成正态分布随机数
tf.truncated_normal()	生成去掉过大偏离点的正态分布随机数
tf.random_uniform()	生成均匀分布随机数
tf.random_uniform()	生成均匀分布随机数
tf.zeros	表示生成全 0 数组
tf.ones	表示生成全 1 数组
tf.fill	表示生成全定值数组
tf.constant	表示生成直接给定值的数组

import tensorflow as tf
w = tf.Variable(tf.random_normal([2,3], stddev=2, mean=0, seed=1))
# => <tf.Variable 'Variable:0' shape=(2, 3) dtype=float32_ref>
w = tf.Variable(tf.truncated_normal([2,3], stddev=2, mean=0, seed=1))
# => <tf.Variable 'Variable_1:0' shape=(2, 3) dtype=float32_ref>
w = tf.random_uniform([2,3], minval=0, maxval=1, dtype=tf.int32, seed=1)
# => Tensor("random_uniform:0", shape=(2, 3), dtype=int32)
w = tf.zeros([3,2], tf.int32)
# => Tensor("zeros:0", shape=(3, 2), dtype=int32)
w = tf.ones([3,2], tf.int32)
# => Tensor("ones:0", shape=(3, 2), dtype=int32)
w = tf.fill([3,2], 6)
# => Tensor("Fill:0", shape=(3, 2), dtype=int32)
w = tf.constant([3,2])
# => Tensor("Const:0", shape=(2,), dtype=int32)

注意：①随机种子如果去掉每次生成的随机数将不一致，②如果没有特殊要求标准差、均值、随机种子是可以不写的。

---

神经网络的搭建

神经网络模型的实现过程：

1. 准备数据集：作为神经网络模型的训练\测试数据
2. 前向传播：搭建模型结构，先搭建计算图，再用会话执行，计算输出
3. 反向传播：模型学习到大量特征数据，迭代优化模型参数
4. 完成训练，验证模型精度

由此可见，基于深度学主要分为两个过程，即训练过程和使用过程。 训练过程是第一步、第二步、第三步的循环迭代，使用过程是第四步，一旦参数优化完成就可以固定这些参数，实现特定应用了。当前很多实际应用中，会优先使用现有的成熟可靠的模型结构，用个人的数据集训练模型，判断是否能对个人数据集作出正确响应，再适当更改网络结构，反复迭代，让机器自动训练参数找出最优结构和参数，以固定专用模型。

前向传播

前向传播就是搭建模型的计算过程，让模型具有推理能力，可以针对一组输入给出相应的输出。
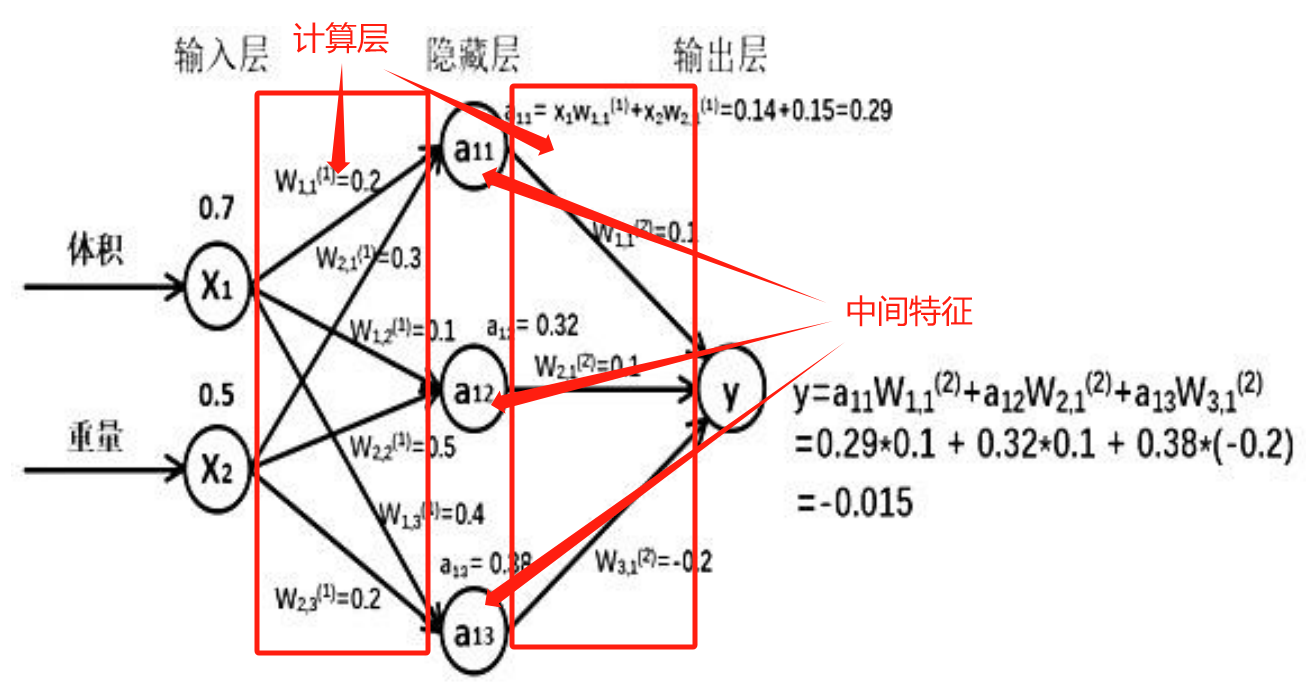
举个案例，假如快递运输费用，体积为 x1，重量为 x2，体积和重量就是我们选择的特征，把它们输入到神经网络，当体积和重量这组数据走过神经网络后会得到一个输出，即费用。
假如输入的特征值是：体积 0.7 重量 0.5：

由图可知，隐藏层节点 a11=x1w11+x2w21=0.14+0.15=0.29，同理算得节点 a12=0.32，a13=0.38，最终计算得到输出层 Y=-0.015，这便实现了前向传播过程。

前向传播过程的 tensorflow 描述：

1. 输入层：$X$是$\mathrm{n}\times 2$的矩阵，表示一次输入$n$组特征，这组特征包含了体积和重量两个元素。

   x = tf.placeholder(tf.float32, shape=(None, 2))
   

2. 隐藏层：$W_{(F\mathrm{rontNodeNumber},R\mathrm{earNodeNumber})}^{(\mathrm{layers})}$是待优化的参数，对于第一计算层的$w^{(1)}$前面有两个节点，后面有三个节点，$w^{(1)}$是个两行三列矩阵：
   $W^{(1)}=\left[\begin{array}{ccc}{w}_{(1,1)}^{(1)}& w_{(1,2)}^{(1)}& w_{(1,3)}^{(1)}\\ w_{(2,1)}^{(1)}& w_{(2,2)}^{(1)}& w_{(2,3)}^{(1)}\end{array}\right]$，即$a^{\left(1\right)}=\left[a_{11},a_{12},a_{13}\right]=X{W}^{(1)}$；
   对于第二计算层的$w^{(2)}$前面有三个节点，后面有1个节点，$w^{(2)}$是个三行一列矩阵：
   $W^{(2)}=\left[\begin{array}{c}{w}_{(1,1)}^{(2)}\\ w_{(2,1)}^{(2)}\\ w_{(3,1)}^{(2)}\end{array}\right]$,即$y=a^{\left(1\right)}{W}^{(1)}$。

   a = tf.matmul(x, w1)
   y = tf.matmul(a, w2)
   

神经网络共有几层(或当前是第几层网络)都是指的计算层，所有的计算层统称为隐藏层，而隐藏层的计算层计算出结果通常称做中间特征，不要错把这些当作隐藏层。

完整的前向传播代码。

import tensorflow as tf

# 定义输入和参数
# 用tf.placeholder定义输入，在sess.run函数中要用feed_dict指定输入
x = tf.placeholder(tf.float32, shape=(None, 2))
w1= tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2= tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))

# 定义前向传播过程
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)

# 汇总所有待优化变量
init_op = tf.global_variables_initializer()

# 调用会话计算结果
# 变量初始化、计算图节点运算都要用会话(with结构)实现
with tf.Session() as sess:
    # 在sess.run函数中变量初始化
    sess.run(init_op)
    # 在sess.run函数中计算图节点运算
    print("the result of tf3_5.py is:\n",sess.run(y, feed_dict={x: [[0.7,0.5],[0.2,0.3],[0.3,0.4],[0.4,0.5]]}))
    print("w1:\n", sess.run(w1))
    print("w2:\n", sess.run(w2))

反向传播

反向传播：训练模型参数，在所有参数上用梯度下降，使 NN 模型在训练数据上的损失函数最小。
反向传播过程的 tensorflow 描述：

1. 损失函数(loss)：计算得到的预测值 y 与已知真实值 y_的误差。均方误差 MSE
   是比较常用的方法之一，它计算前向传播求出的预测值与已知真实值之差的平方再求平均：$$MSE(y\_,y)=\frac{{\sum }_{i=1}^n{(y-y\_)}^2}{n}$$

   loss_mse = tf.reduce_mean(tf.square(y-y_)) 
   

2. 反向传播优化方法：以减小 loss 值为优化目标，常见的三种有随机梯度下降、momentum 优化器、adam优化器等优化方法。

   # 学习率(learning_rate):决定每次参数更新的幅度。
   train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss) 
   train_step = tf.train.MomentumOptimizer(learning_rate, momentum).minimize(loss) 
   train_step = tf.train.AdamOptimizer(learning_rate).minimize(loss)
   

   方法	功能
   tf.train.GradientDescentOptimizer()	梯度下降用于最小化损失函数。它通过计算损失函数关于每个可训练参数的梯度，并将参数沿着梯度的反方向进行更新，以减少损失函数的值。
   tf.train.MomentumOptimizer()	动量优化器在梯度下降的基础上引入了动量的概念，以加速训练过程，它通过累积之前梯度的方向来更新参数，以减少损失函数的值。
   tf.train.AdamOptimizer()	结合了动量优化器和自适应学习率的思想。它根据梯度的平均值和方差来自适应地调整学习率，以在训练过程中更好地适应不同参数的变化，以减少损失函数的值。

完整的反向传播代码。

# coding:utf-8
# 0导入模块，生成模拟数据集。
import tensorflow as tf
import numpy as np

# 每次训练的数量
BATCH_SIZE = 8
SEED = 23455

# 基于seed产生随机数
rdm = np.random.RandomState(SEED)
# 随机数返回32行2列的矩阵 表示32组 体积和重量 作为输入数据集
X = rdm.rand(32, 2)
# 从X这个32行2列的矩阵中 取出一行 判断如果和小于1 给Y赋值1 如果和不小于1 给Y赋值0
# 作为输入数据集的标签(正确答案)
Y_ = [[int(x0*0.5+x1*0.8)] for (x0, x1) in X]

# 定义神经网络的输入、参数和输出,定义前向传播过程。
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))

w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))

a = tf.matmul(x, w1)
y = tf.matmul(a, w2)

# 定义损失函数及反向传播方法。
loss_mse = tf.reduce_mean(tf.square(y - y_))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss_mse)
# train_step = tf.train.MomentumOptimizer(0.001,0.9).minimize(loss_mse)
# train_step = tf.train.AdamOptimizer(0.001).minimize(loss_mse)

# 生成会话，训练STEPS轮
with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    # 输出目前（未经训练）的参数取值。
    print("w1:\n", sess.run(w1))
    print("w2:\n", sess.run(w2))

    # 训练模型
    # 悬链次数
    STEPS = 3000
    for i in range(STEPS):
    	# 随机选取一组batchsize为8的数据段
        start = (i * BATCH_SIZE) % 32
        end = start + BATCH_SIZE
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y_[start:end]})
        if i % 500 == 0:
            total_loss = sess.run(loss_mse, feed_dict={x: X, y_: Y_})
            print("After %d training step(s), loss_mse on all data is %g" % (i, total_loss))

    # 输出训练后的参数取值。
    print("w1:\n", sess.run(w1))
    print("w2:\n", sess.run(w2))

---

总结

梳理出神经网络搭建的八股，搭建过程分四步完成：准备工作、前向传播、反向传播和循环迭代：

1. 导入模块，生成模拟数据集；
2. 前向传播：定义输入、参数和输出；
3. 反向传播：定义损失函数、反向传播方法；
4. 生成会话，训练n轮。