堆栈（Stack）和队列（Queue）是两种非常重要的数据结构，两者都是特殊的线性表：对于堆栈，所有的插入和删除（以至几乎所有的存取）都是在表的同一端进行；而对于队列来说，所有的插入都是在表的一端进行，所有的删除（以至几乎所有的存取）都是在表的另一端进行。

一、堆栈

1. 定义

  堆栈（简称栈）是一种操作受限的线性表，只允许在表的同一端进行插入和删除操作，且这些操作是按后进先出的原则进行的。进行插入和删除的一端被称为栈顶，另一端被称为栈底。当栈中无元素时称其为空栈。根据上述定义，每次删除（退栈）的总是最后插入（进栈）的元素。

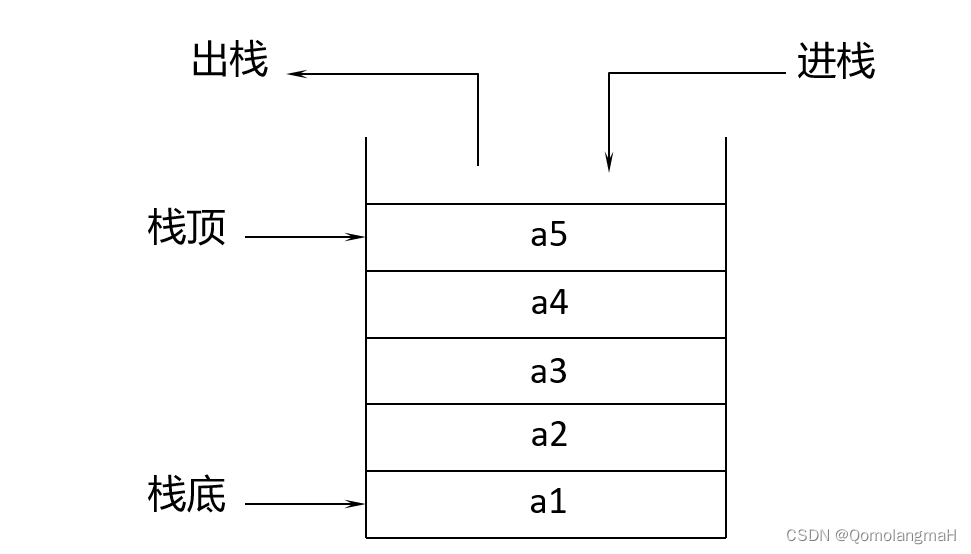
  如图所示的堆栈中，诸元素以a1，a2，a3，a4，a5的顺序进栈，而退栈的次序则是a5，a4，a3，a2，a1。 也就是说，从栈中取走元素是按后进先出的原则进行的，因此栈又被称作后进先出（Last in First Out）的线性表，简称为LIFO表。

2. 基本操作

• 堆栈是受限的线性表，其基本操作包括

  • IsEmpty ( ) : 判断栈是否为空；
  • push ( ) : 压入一个元素（插入）；
  • pop ( ) : 弹出一个元素（删除）；
  • peek ( ) : 存取栈顶元素值；
  • clear ( ) : 清空栈；

• 同普通线性表一样，堆栈也可以用顺序存储和链接存储两种方式来实现：

二、顺序栈

  参考前文：线性表（六）堆栈：顺序栈及其基本操作（初始化、判空、判满、入栈、出栈、存取栈顶元素、清空栈）

三、链式栈

  用数组实现的栈效率很高，但若同时使用多个栈，顺序栈将浪费很多空间。用单链表来实现栈可避免这个问题，其代价是要为每个栈元素分配一个额外的指针空间（存放指针域）。
  用单链表实现堆栈，首先要考虑栈顶对应链表的表头还是表尾。因为堆栈主要操作（插入、删除、存取）的对象是栈顶元素，若栈顶对应表尾，则每次栈顶操作都要对单链表进行遍历，其时间复杂性为O(n)（设链表的长度为n）；若栈顶对应表头，则每个操作的时间复杂性是O(1)，显然，栈顶对应表头是合理的。

0. 链表

  参考前文：线性表（二）单链表及其基本操作（创建、插入、删除、修改、遍历打印）

1. 头文件和常量

   #include <stdio.h>
   #include <stdlib.h>

• 两个头文件
  • stdio.h用于输入输出操作
  • stdlib.h用于内存分配和释放

2. 栈结构体

typedef struct Node {
    int data;
    struct Node* next;
} Node;

typedef struct {
    Node* top;
} Stack;

• Node 结构体用于表示堆栈中的节点，包含一个整型数据成员 data 和一个指向下一个节点的指针 next。
• Stack 结构体用于表示堆栈，只包含一个指向堆栈顶部节点的指针 top。

3. 栈的初始化

void init(Stack* stack) {
    stack->top = NULL;
}

  init 函数用于初始化堆栈，将 stack 的 top 指针设为 NULL，表示堆栈为空。

4. 判断栈是否为空

  isEmpty 函数判断堆栈是否为空，如果 stack 的 top 指针为 NULL，则返回 1（表示真），否则返回 0（表示假）。

int isEmpty(Stack* stack) {
    return stack->top == NULL;
}

5. 入栈

void push(Stack* stack, int value) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    newNode->data = value;
    newNode->next = stack->top;
    stack->top = newNode;
}

   push 函数用于将元素压入堆栈。

• 创建一个新的节点 newNode：
  • 将传入的值 value 赋给 newNode 的 data 成员；
  • 将 newNode 的 next 指针指向当前堆栈的顶部节点；
• 更新堆栈的 top 指针为 newNode，使其成为新的顶部节点。

6. 出栈

int pop(Stack* stack) {
    if (isEmpty(stack)) {
        printf("Stack is empty. Cannot pop element.\n");
        return -1;
    }
    Node* topNode = stack->top;
    int value = topNode->data;
    stack->top = topNode->next;
    free(topNode);
    return value;
}

  pop 函数用于从堆栈中弹出（删除并返回）顶部元素。

• 检查堆栈是否为空：
  • 如果为空，则打印一条错误消息并返回 -1；
  • 否则，它获取堆栈顶部节点的值 value；
• 更新堆栈的 top 指针为原顶部节点的下一个节点，释放原顶部节点的内存，并返回 value。

7. 存取栈顶元素

int peek(Stack* stack) {
    if (isEmpty(stack)) {
        printf("Stack is empty. Cannot peek element.\n");
        return -1;
    }
    return stack->top->data;
}

  peek 函数用于查看堆栈顶部元素的值，但不对堆栈进行修改。

• 首先检查堆栈是否为空：
  • 如果为空，则打印一条错误消息并返回 -1；
  • 否则，它直接返回堆栈顶部节点的值。

8. 清空栈

void clear(Stack* stack) {
    Node* current = stack->top;
    while (current != NULL) {
        Node* temp = current;
        current = current->next;
        free(temp);
    }
    stack->top = NULL;
}

  clear 函数用于清空堆栈，即释放堆栈中所有节点的内存。它通过遍历堆栈，从顶部节点开始，逐个释放节点的内存，直到堆栈为空。

9. 主函数

int main() {
    Stack stack;
    init(&stack);

    push(&stack, 10);
    push(&stack, 20);
    push(&stack, 30);

    printf("Top element: %d\n", peek(&stack));

    printf("Popped element: %d\n", pop(&stack));
    printf("Popped element: %d\n", pop(&stack));

    printf("Is stack empty? %s\n", isEmpty(&stack) ? "Yes" : "No");

    clear(&stack);

    printf("Is stack empty? %s\n", isEmpty(&stack) ? "Yes" : "No");

    return 0;
}

• 创建一个 Stack 类型的变量 stack，然后通过调用 init 函数将其初始化为空堆栈。
• 接下来，通过连续调用 push 函数，将值 10、20 和 30 压入堆栈。
• 使用 peek 函数查看堆栈的顶部元素。
• 使用 pop 函数两次弹出堆栈的元素。
• 使用 isEmpty 函数判断堆栈是否为空。
• 调用 clear 函数清空堆栈中的所有元素。
• 再次使用 isEmpty 函数判断堆栈是否为空。

10. 代码整合

#include <stdio.h>
#include <stdlib.h>

typedef struct Node {
    int data;
    struct Node* next;
} Node;

typedef struct {
    Node* top;
} Stack;

void init(Stack* stack) {
    stack->top = NULL;
}

int isEmpty(Stack* stack) {
    return stack->top == NULL;
}

void push(Stack* stack, int value) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    newNode->data = value;
    newNode->next = stack->top;
    stack->top = newNode;
}

int pop(Stack* stack) {
    if (isEmpty(stack)) {
        printf("Stack is empty. Cannot pop element.\n");
        return -1;
    }
    Node* topNode = stack->top;
    int value = topNode->data;
    stack->top = topNode->next;
    free(topNode);
    return value;
}

int peek(Stack* stack) {
    if (isEmpty(stack)) {
        printf("Stack is empty. Cannot peek element.\n");
        return -1;
    }
    return stack->top->data;
}

void clear(Stack* stack) {
    Node* current = stack->top;
    while (current != NULL) {
        Node* temp = current;
        current = current->next;
        free(temp);
    }
    stack->top = NULL;
}

int main() {
    Stack stack;
    init(&stack);

    push(&stack, 10);
    push(&stack, 20);
    push(&stack, 30);

    printf("Top element: %d\n", peek(&stack));

    printf("Popped element: %d\n", pop(&stack));
    printf("Popped element: %d\n", pop(&stack));

    printf("Is stack empty? %s\n", isEmpty(&stack) ? "Yes" : "No");

    clear(&stack);

    printf("Is stack empty? %s\n", isEmpty(&stack) ? "Yes" : "No");

    return 0;
}

四、 顺序栈与链式栈的比较

  在空间复杂性上，顺序栈在创建时就申请了数组空间，若栈经常处于不满状态将造成存储空间的浪费；链式栈所需空间是根据需要随时申请的，比之顺序栈仅仅是其每个结点需要额外的空间以存储其next指针域。
  在时间复杂性上，对于针对栈顶的基本操作（压入、弹出和栈顶元素存取），容易看出，顺序栈和链式栈的时间复杂性均为O(1) 。