---

引言

对数理统计的一些基本概念有了了解后，我们来学习三个重要的抽样分布。

---

一、${\chi }^2$ 分布

1.1 ${\chi }^2$ 分布定义

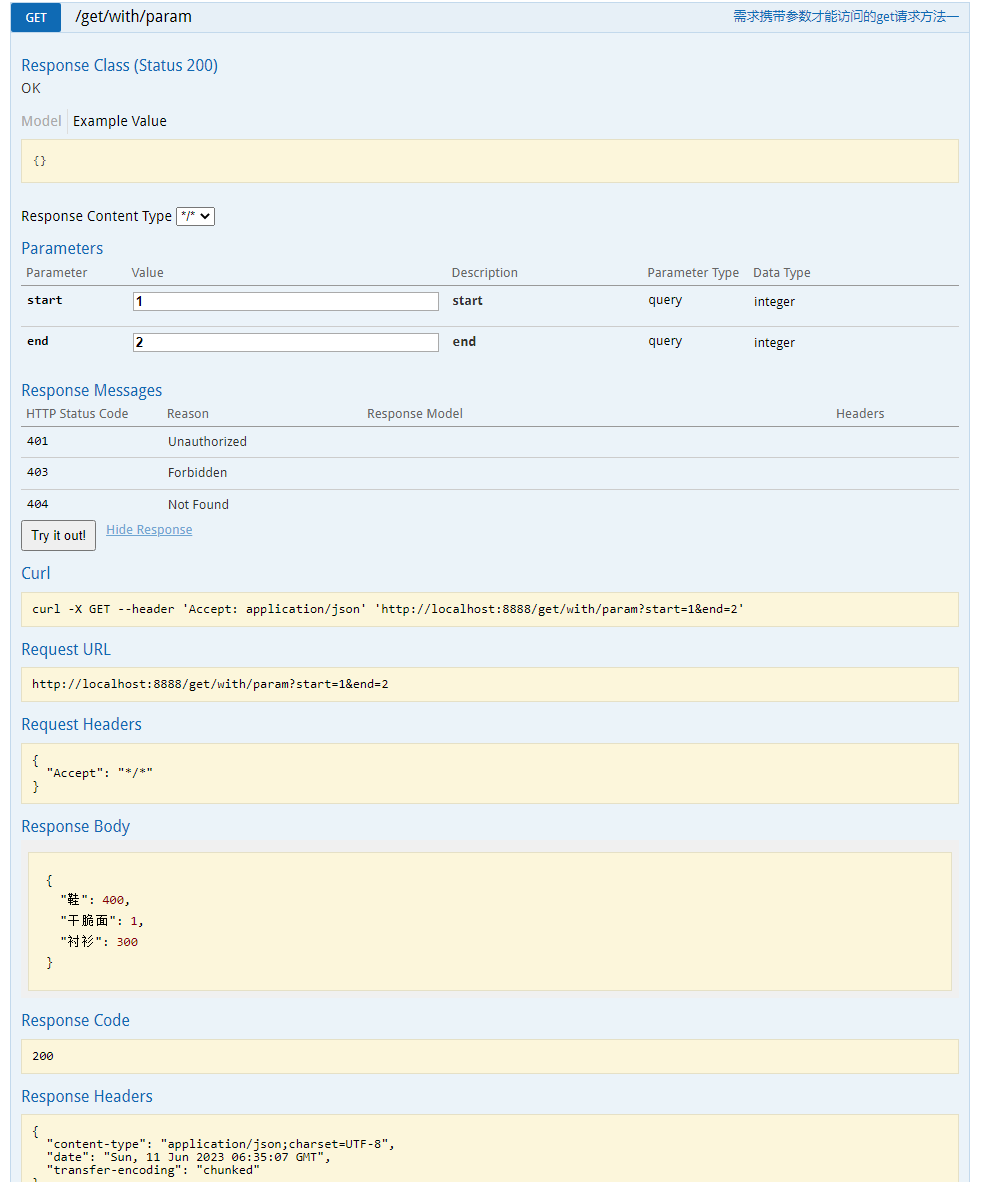
设 $X_1,X_2,\cdots ,X_n$ 相互独立且均服从标准正态分布 $N(0,1)$ ，称 $X_1^2+X_2^2+\cdots +X_n^2$ 服从 ${\chi }^2(n)$ ，其中 $n$ 称为自由度。设其概率密度为 $f(x)$ ，则其函数图像为：

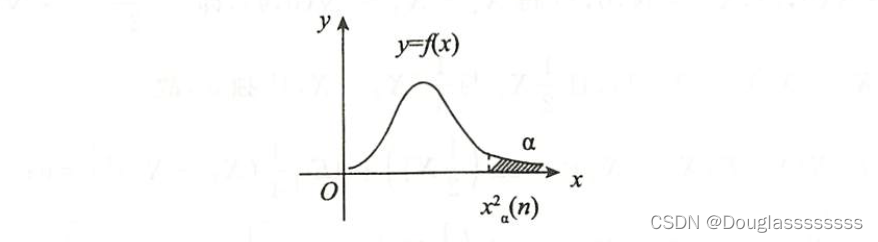
对任意的 $0<\alpha <1$ ，若 P { X > χ α 2 ( n ) } = α , P\{X>\chi_\alpha^2(n)\}=\alpha, P{X>χα2​(n)}=α, 称 ${\chi }_{\alpha }^2(n)$ 为 ${\chi }^2(n)$ 分布的右或上 $\alpha$ 分位点。若有 P { X < χ 1 − α 2 ( n ) } = α , P\{X<\chi_{1-\alpha}^2(n)\}=\alpha, P{X<χ1−α2​(n)}=α, 称 ${\chi }_{1-\alpha }^2(n)$ 为 ${\chi }^2(n)$ 分布的左或下 $\alpha$ 分位点，如下图所示。

1.2 性质

1. 若 $X\sim N(0,1)$ ，则 $X^2\sim {\chi }^2(1);$
2. 若 $X\sim {\chi }^2(m),Y\sim {\chi }^2(n)$ ，且 $X,Y$ 相互独立，则 $X+Y\sim {\chi }^2(m+n);$
3. 若 $X\sim {\chi }^2(n)$ ，则 $E(X)=n,D(X)=2n.$

对性质 3 进行证明：

由 $X\sim {\chi }^2(n)$ ，则 $X=X_1^2+X_2^2+\cdots +X_n^2$ ，其中 $X_i\sim N(0,1)(i=1,2,\cdots ,n)$ ，有 $E(X_i)=0,D(X_i)=1$ 。根据方差的定义，$E(X_i^2)=D(X_i)+[E(X_i){]}^2=1$ 。计算 $$E(X_i^4)={\int }_{-\infty }^{+\infty }{x}^4\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}}dx=\frac{2}{\sqrt{2\pi }}{\int }_0^{+\infty }{x}^4{e}^{-\frac{x^2}{2}}dx.$$ 换元，令 $t=x^2/2$ ，有 $$E(X_i^4)=\frac{2}{\sqrt{2\pi }}{\int }_0^{+\infty }4t^2{e}^{-t}\cdot \frac{1}{\sqrt{2t}}dt=\frac{4}{\sqrt{\pi }}{\int }_0^{+\infty }{t}^{\frac{3}{2}}{e}^{-t}dt.$$ 回忆一下，在反常积分，我们学过一个伽玛函数，即$$\Gamma (\alpha )={\int }_0^{+\infty }{x}^{\alpha -1}{e}^{-x}dx（\alpha >0）$$ 主要有如下性质：$$\Gamma (\alpha +1)=\alpha \Gamma (\alpha ),\Gamma (n+1)=n!,\Gamma (\frac{1}{2})=\sqrt{\pi }.$$ 因此，我们可以得到 $E(X_i^4)=4/\sqrt{\pi }\cdot \Gamma (5/2)=4/\sqrt{\pi }\cdot 3/2\cdot \sqrt{\pi }/2=3.$ 于是我们可以得到：$D(X_i^2)=E(X_i^4)-[E(X_i^2){]}^2=3-1=2.$ 故 $E(X)=\sum E(X_i^2)=n,D(X)=\sum D(X_i^2)=2n.$

【例题】设总体 $X\sim N(0,2)$, ($X_1,X_2,X_3)$ 为总体 $X$ 的简单随机样本，记 $Z=X_1^2+(X_2-X_3{)}^2$，求 $E(Z),D(Z)$ 。

解： 要想利用 ${\chi }^2$ 分布，必须有标准正态分布，因此可将 $X_1$ 标准化，即 $X_1/\sqrt{2}\sim N(0,1)$，于是有 $X_1^2/2\sim {\chi }^2(1)$ 。
$X_2-X_3\sim N(0,4)$ ，故 $(X_2-X_3)/2\sim N(0,1)$ ，从而有 $(X_2-X_3{)}^2/4\sim {\chi }^2(1)$ 。
于是有 $E(Z)=E(X_1^2)+E[(X_2-X_3{)}^2]=2E(X_1^2/2)+4E[(X_2-X_3{)}^2/4]=2+4=6,D(Z)=4D(X_1^2/2)+16D[(X_2-X_3{)}^2/4]=8+32=40.$

---

二、$t$ 分布

2.1 定义

设 $X\sim N(0,1),Y\sim {\chi }^2(n)$ ，且 $X,Y$ 相互独立，称 $$\frac{X}{\sqrt{\frac{Y}{n}}}$$ 服务自由度为 $n$ 的 $t$ 分布，记为 $X/\sqrt{Y/n}\sim t(n)$ 。

设 $X\sim t(n)$ ，其概率密度函数为 $f(x)$ ，对任意的 $0<\alpha <1$ ，若 P { X > t α ( n ) } = α , P\{X>t_\alpha(n)\}=\alpha, P{X>tα​(n)}=α, 称 $t_{\alpha }(n)$ 为 $t(n)$ 分布的右或上 $\alpha$ 分位点。

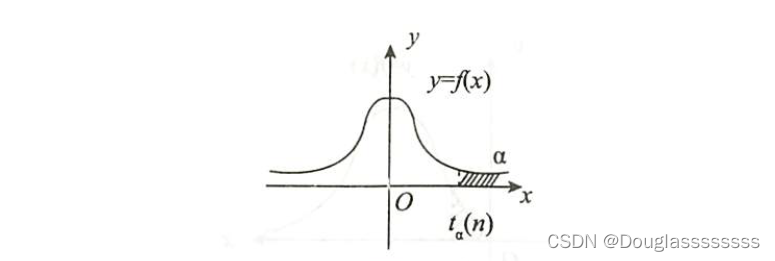
若有 P { X < t 1 − α ( n ) } = α , P\{X<t_{1-\alpha}(n)\}=\alpha, P{X<t1−α​(n)}=α, 称 $t_{1-\alpha }(n)$ 为 $t(n)$ 分布的左或下 $\alpha$ 分位点。显然，有 $t_{1-\alpha }(n)=-t_{\alpha }(n)$ 。

2.2 性质

1. 若 $X\sim t(n)$，则 $X$ 的概率密度为偶函数，且有 P { X < 0 } = P { X ≥ 0 } = 0.5 ; P\{X<0\}=P\{X\geq0\}=0.5; P{X<0}=P{X≥0}=0.5;
2. 若 $X\sim t(n)$，则 $E(X)=0,D(X)=n/(n-2),(n>2);$
3. 若 $X\sim t(n)$，则 $X$ 近似服从标准正态分布。

---

三、$F$ 分布

3.1 定义

设 $X\sim {\chi }^2(m),Y\sim {\chi }^2(n)$ ，且 $X,Y$ 独立，则称 $$\frac{X/m}{Y/n}$$ 服从自由度为 $m,n$ 的 $F$ 分布，记为 $(X/m)/(Y/n)\sim F(m,n)$ 。

设 $X\sim F(m,n)$ ，其概率密度函数为 $f(x)$ ，对任意的 $0<\alpha <1$ ，若 P { X > F α ( m , n ) } = α , P\{X>F_\alpha(m,n)\}=\alpha, P{X>Fα​(m,n)}=α, 称 $F_{\alpha }(m,n)$ 为 $F(m,n)$ 分布的右或上 $\alpha$ 分位点。如下图所示。

若有 P { X < F 1 − α ( m , n ) } = α , P\{X<F_{1-\alpha}(m,n)\}=\alpha, P{X<F1−α​(m,n)}=α, 称 $F_{1-\alpha }(m,n)$ 为 $F(m,n)$ 分布的左或下 $\alpha$ 分位点。

3.2 性质

1. 若 $X\sim F(m,n)$ ，则 $1/X\sim F(n,m)$ ；
2. 若 $X\sim t(m)$ ，则 $X^2\sim F(1,m)$ ；
   证明： 由 $X\sim t(m)$ ，则存在 $U\sim N(0,1),V\sim {\chi }^2(m)$ ，且 $U,V$ 相互独立，且 $$X=U/\sqrt{V/m},$$ 于是 $X^2=U^2/(V/m)$ ，即 $X^2=(U^2/1)/(V/m)$ ；$U^2\sim {\chi }^2(1)$ 且 $U^2,V$ 相互独立，故 $X^2\sim F(1,m)$ 。
3. 对 $0<\alpha <1$ ，有 $F_{\alpha }(m,n)=1/F_{1-\alpha }(n,m)$ 。
   证明： 由性质 1 ，$1/X\sim F(n,m)$ ，故有 P { 1 / X > F 1 − α ( n , m ) } = 1 − α = P { X < 1 / F 1 − α ( n , m ) } = P { X < F α ( m , n ) } P\{1/X>F_{1-\alpha}(n,m)\}=1-\alpha=P\{X<1/F_{1-\alpha}(n,m)\}=P\{X<F_\alpha(m,n)\} P{1/X>F1−α​(n,m)}=1−α=P{X<1/F1−α​(n,m)}=P{X<Fα​(m,n)} ，即 $F_{\alpha }(m,n)=1/F_{1-\alpha }(n,m)$ 。

---

写在最后

这三个分布彼此之间都是有一定联系的，同时也都跟标准正态有关，把握住他们的联系，应该就能应付考试了。