【TensorFlow1.X】系列学习笔记【基础一】

大量经典论文的算法均采用 TF 1.x 实现, 为了阅读方便, 同时加深对实现细节的理解, 需要 TF 1.x 的知识

文章目录

【TensorFlow1.X】系列学习笔记【基础一】
前言
线性回归
非线性回归
逻辑回归
总结

前言

本篇博主将用最简洁的代码由浅入深实现几个小案例，让读者直观体验最基础的数据的处理、模型的设计以及模型的优化。【代码参考】

线性回归

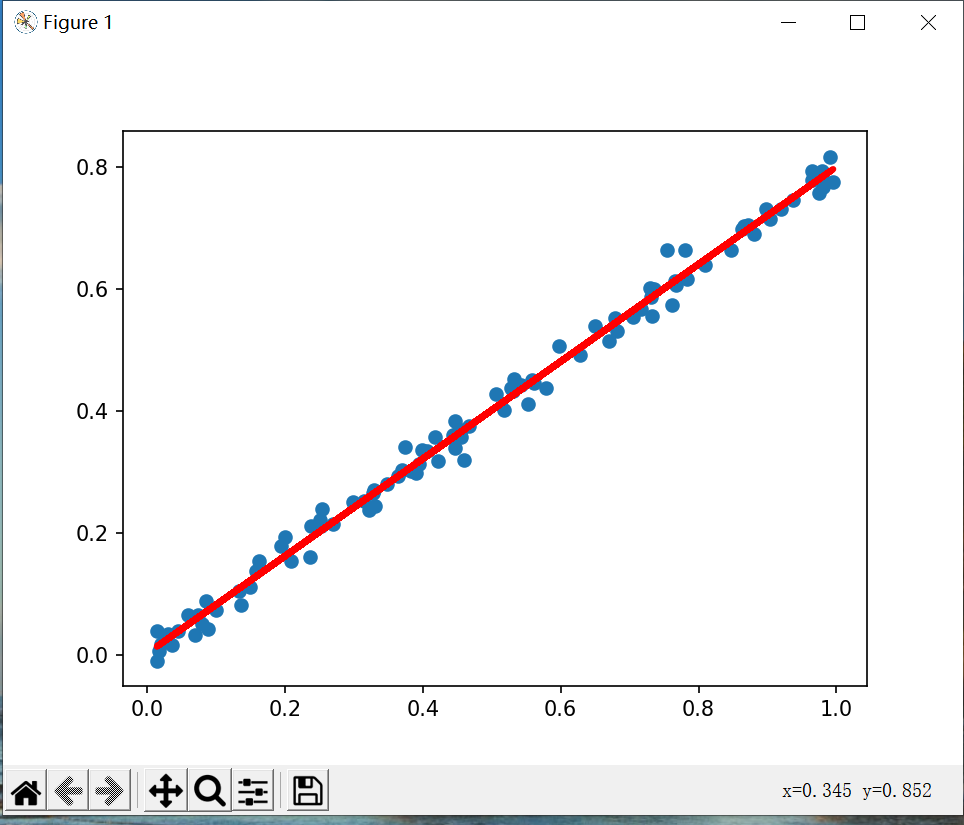
线性回归是一种常见回归分析方法，它假设目标值与特征之间存在线性关系。线性回归模型通过拟合线性函数来预测目标值。线性回归模型的形式比较单一的，即满足一个多元一次方程。常见的线性方程如： ${\rm{y}} = w \times x + b$ ，但是观测到的数据往往是带有噪声，于是给现有的模型一个因子 $\varepsilon$ ，并假设该因子符合标准正态分布： ${\rm{y}} = w \times x + b + \varepsilon$ 。对于线性模型，深度学习可以通过构建单层神经网络来描述,这个单层神经网络通常被称为全连接层(Fully Connected Layer)或线性层(Linear Layer)，其中每个神经元都与上一层的所有神经元相连接，且没有非线性激活函数。

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

# 随机生成100个数据点,服从“0~1”均匀分布
x_data = np.random.rand(100)

# 提升维度(100)-->(100,1)
x_data = x_data[:, np.newaxis]

# 制作噪声,shape与x_data一致
noise = np.random.normal(0, 0.02,  x_data.shape)

# 构造目标公式
y_data = 0.8 * x_data + 0.1 + noise

# 输入层:placeholder用于接收训练的数据
x = tf.placeholder(tf.float32, [None, 1], name="x_input")
y = tf.placeholder(tf.float32, [None, 1], name="y_input")

# 构造线性模型
b = tf.Variable(0., name="bias")
w = tf.Variable(0., name="weight")
out = w * x_data + b

# 构建损失函数
loss = 1/2*tf.reduce_mean(tf.square(out - y))
# print(loss)

# 定义优化器
optim = tf.train.GradientDescentOptimizer(0.1)
# print(optim)

# 最小化损失函数
train_step = optim.minimize(loss)

# 初始化全部的变量
init = tf.global_variables_initializer()

# 训练迭代
with tf.Session() as sess:
    sess.run(init)
    for step in range(2000):
        sess.run([loss, train_step], {x: x_data, y: y_data})
        if step % 200 == 0:
            w_value, b_value, loss_value = sess.run([w, b, loss], {x: x_data, y: y_data})
            print("step={}, k={}, b={}, loss={}".format(step, w_value, b_value, loss_value))
    prediction_value = sess.run(out, feed_dict={x: x_data})

plt.figure()
plt.scatter(x_data, y_data)
plt.plot(x_data, prediction_value, "r-", lw=3)
plt.show()

非线性回归

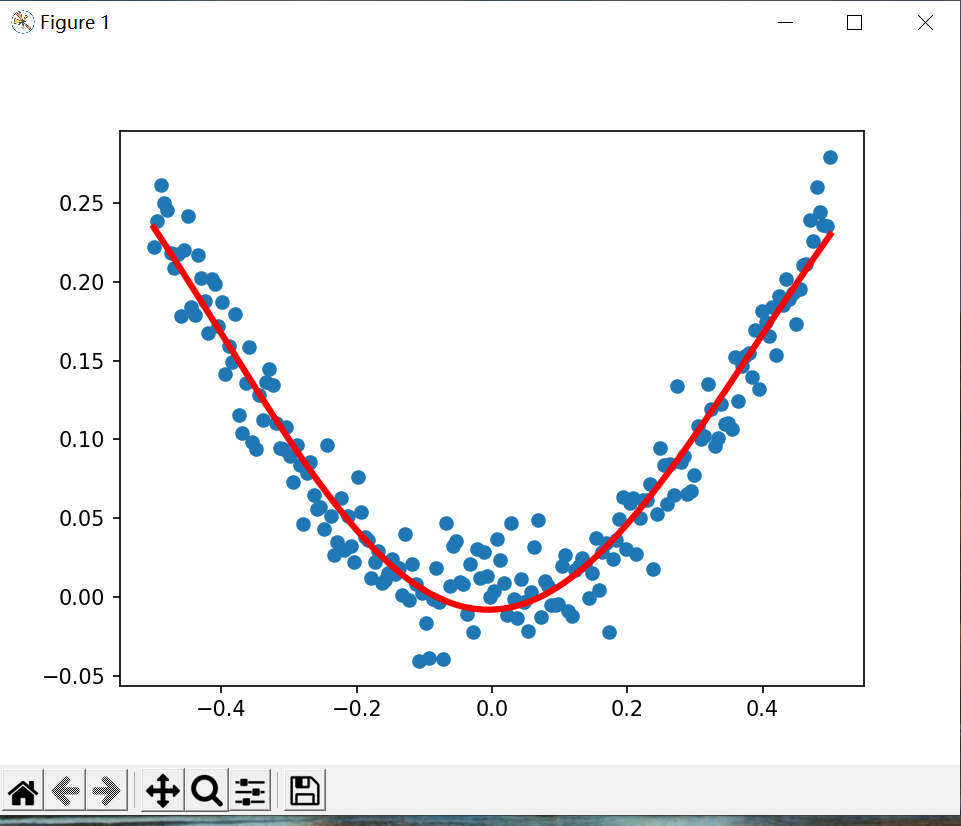
非线性回归也是一种常见回归分析方法，它假设目标值与特征之间存在非线性关系。与线性回归不同，非线性回归模型可以拟合复杂的非线性关系。通过拟合非线性函数到数据中，非线性回归模型可以找到最佳的函数参数，以建立一个能够适应数据的非线性关系的模型。非线性回归模型的形式可以是多项式函数、指数函数、对数函数、三角函数等任意形式的非线性函数，这些函数可以包含自变量的高次项、交互项或其他非线性变换。常见的非线性方程如： ${\rm{y}} = {x^2}$ ，但是观测到的数据往往是带有噪声，于是给现有的模型一个因子 $\varepsilon$ ，并假设该因子符合标准正态分布： ${\rm{y}} = {x^2} + \varepsilon$ 。深度学习模型通常由多个神经网络层组成，每一层都包含许多神经元。每个神经元接收来自前一层的输入，并通过激活函数对输入进行非线性转换，然后将结果传递给下一层，通过多个层的堆叠，深度学习模型可以学习到多个抽象层次的特征表示。

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

# 生成200个数据点,从“-0.5~0.5”均匀排布
x_data = np.linspace(-0.5, 0.5, 200)

# 提升维度(200)-->(200,1)
x_data = x_data[:, np.newaxis]

# 制作噪声,shape与x_data一致
noise = np.random.normal(0, 0.02,  x_data.shape)

# 构造目标公式
y_data = np.square(x_data) + noise

# 输入层:placeholder用于接收训练的数据
x = tf.placeholder(tf.float32, [None, 1], name="x_input")
y = tf.placeholder(tf.float32, [None, 1], name="y_input")

# 隐藏层
W_1 = tf.Variable(tf.random_normal([1, 10]))
b_1 = tf.Variable(tf.zeros([1, 10]))
a_1 = tf.matmul(x, W_1) + b_1
out_1 = tf.nn.tanh(a_1)

# 输出层
W_2 = tf.Variable(tf.random_normal([10, 1]))
b_2 = tf.Variable(tf.zeros([1, 1]))
a_2 = tf.matmul(out_1, W_2) + b_2
out_2 = tf.nn.tanh(a_2)

# 构建损失函数
loss = 1/2*tf.reduce_mean(tf.square(out_2- y))

# 定义优化器
optim = tf.train.GradientDescentOptimizer(0.1)

# 最小化损失函数
train_step = optim.minimize(loss)

# 初始化全部的变量
init = tf.global_variables_initializer()

# 训练
with tf.Session() as sess:
    sess.run(init)
    for epc in range(10000):
        sess.run([loss, train_step], {x:x_data,y:y_data})
        if epc % 1000 == 0:
            loss_value = sess.run([loss], {x:x_data,y:y_data})
            print("epc={}, loss={}".format(epc, loss_value))
    prediction_value = sess.run(out_2, feed_dict={x:x_data})

plt.figure()
plt.scatter(x_data, y_data)
plt.plot(x_data, prediction_value, "r-", lw=3)
plt.show()

逻辑回归

逻辑回归是一种用于分类问题的统计模型，它假设目标变量与特征之间存在概率关系。逻辑回归模型通过线性函数和逻辑函数的组合来建模概率，以预测样本属于某个类别的概率。逻辑回归本身是一个简单的线性分类模型，但深度学习可以自动地学习特征表示，并通过多层非线性变换来模拟更复杂的关系。MNIST数据集通常被认为是深度学习的入门级别任务之一，可以帮助初学者熟悉深度学习的基本概念、模型构建和训练过程。虽然MNIST是一个入门级别的任务，但它并不能完全代表实际应用中的复杂视觉问题。在实践中，还需要面对更大规模的数据集、多类别分类、图像分割、目标检测等更具挑战性的问题。

import numpy as np
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt

# 载入数据集:首次调用时自动下载数据集(MNIS 数据集)并将其保存到指定的目录中。
mnist = input_data.read_data_sets("MNIST", one_hot=True)

# 设置batch_size的大小
batch_size = 50
# (几乎)所有数据集被用于训练所需的次数
n_batchs = mnist.train.num_examples // batch_size

# 输入层:placeholder用于接收训练的数据
# 这里图像大小是28×28,对数据集进行压缩28×28=782
x = tf.placeholder(tf.float32, [None, 784],name="x-input")
# 10分类(数字0~9)
y = tf.placeholder(tf.float32, [None, 10], name="y-input")

# 隐藏层
w = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([1,10]))
# 全连接层
prediction = tf.matmul(x, w) + b
prediction_softmax = tf.nn.softmax(prediction)
# 交叉熵损失函数+计算张量在指定维度(默认0维)上的平均值
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=prediction, labels=y))

# 定义优化器
optim = tf.train.GradientDescentOptimizer(0.01)

# 最小化损失函数
train_step = optim.minimize(loss)

# 初始化全部的变量
init = tf.global_variables_initializer()

# 计算准确率:选择概率最大的数字作为预测值与真实值进行比较,统计正确的个数再计算准确率
correct_prediction = tf.equal(tf.argmax(prediction_softmax, 1), tf.argmax(y, 1))
accuarcy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

# GPU使用和显存分配:最大限度为1/3
gpu_options = tf.GPUOptions(per_process_gpu_memory_fraction=0.333)
# 用于配置 GPU
sess = tf.Session(config=tf.ConfigProto(gpu_options=gpu_options))

epoch_arr = np.array([])
acc_arr = np.array([])
loss_arr = np.array([])

with tf.Session() as sess:
    sess.run(init)
    # 训练总次数
    for epoch in range(200):
        # 每轮训练的迭代次数
        for batch in range(n_batchs):
            batch_x, batch_y = mnist.train.next_batch(batch_size)
            sess.run([train_step],{x:batch_x, y: batch_y})
        # 用训练集每完成一次训练,则用测试集验证
        acc, los = sess.run([accuarcy, loss], feed_dict = {x:mnist.test.images, y:mnist.test.labels})
        epoch_arr= np.append(epoch_arr, epoch)
        acc_arr = np.append(acc_arr, acc)
        loss_arr = np.append(loss_arr, los)
        print("epoch: ", epoch, "acc: ",acc, "loss: ", los)

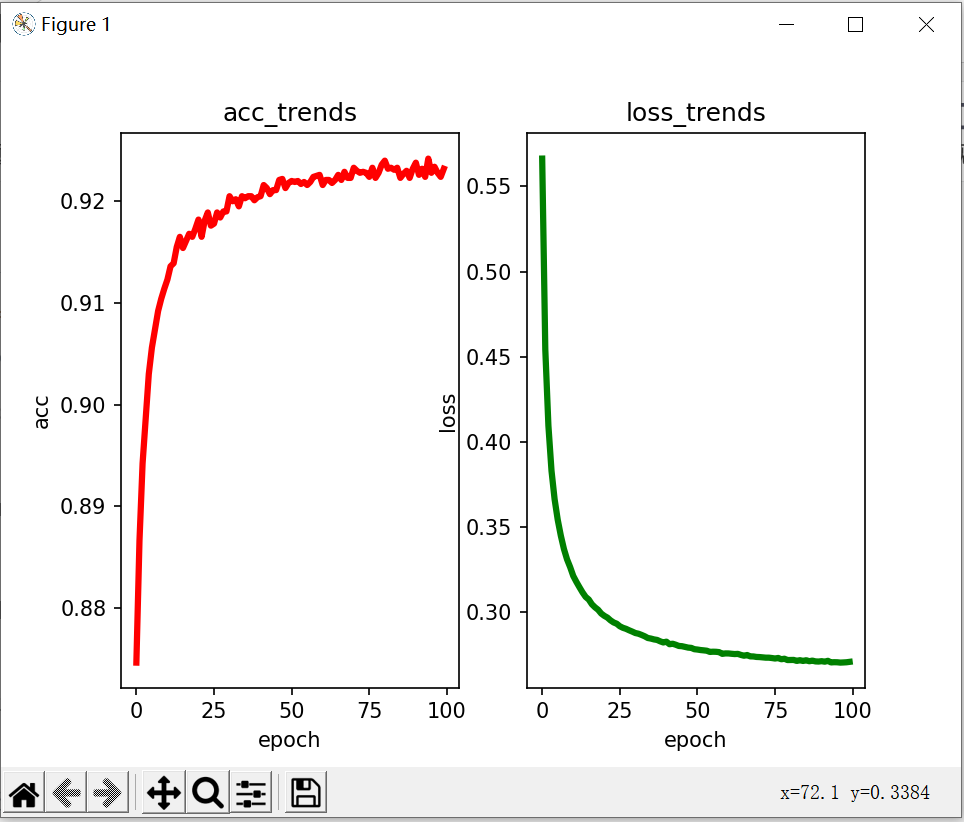
# 分别显示精度上升趋势和损失下降趋势
fig, (ax1, ax2) = plt.subplots(1, 2)

ax1.set_title('acc_trends')
ax1.set_xlabel('epoch')
ax1.set_ylabel('acc')
ax1.plot(epoch_arr, acc_arr, "r-", lw=3)

ax2.set_title('loss_trends')
ax2.set_xlabel('epoch')
ax2.set_ylabel('loss')
ax2.plot(epoch_arr, loss_arr, "g-", lw=3)
plt.show()

总结

训练深度学习模型通常需要大量的标记数据和计算资源。一种常用的训练算法是反向传播算法，它通过最小化损失函数来优化模型参数。常见的损失函数是均方误差损失函数和交叉熵损失函数，可以度量模型输出的概率分布与实际标签之间的差异。在实际应用中，深度学习通常用于处理非线性回归，而逻辑回归和线性回归则是其中的一些特殊情况。