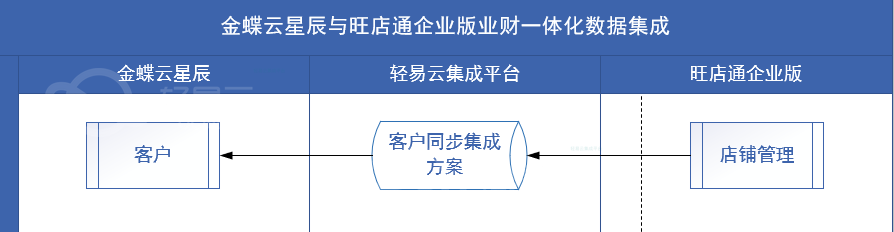
一.效果

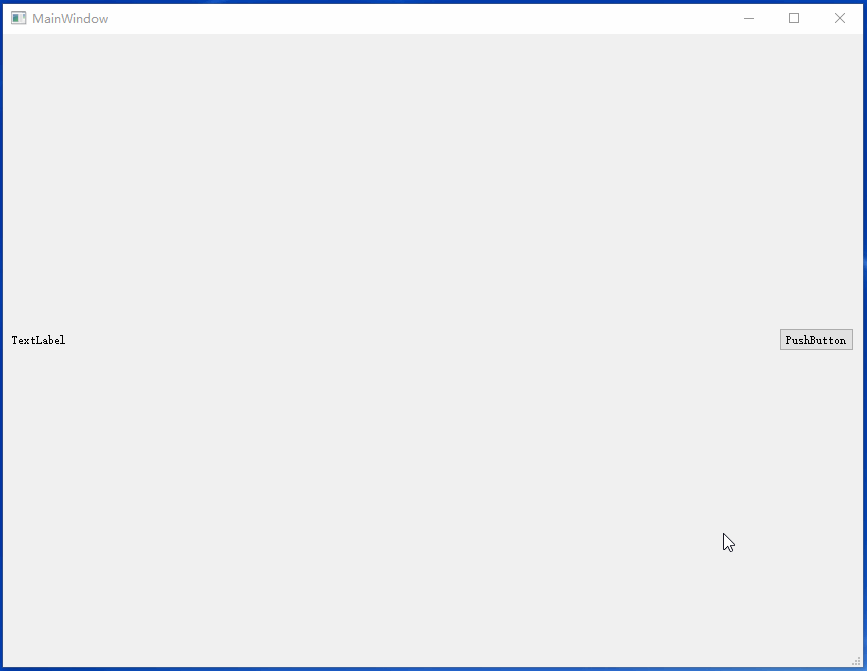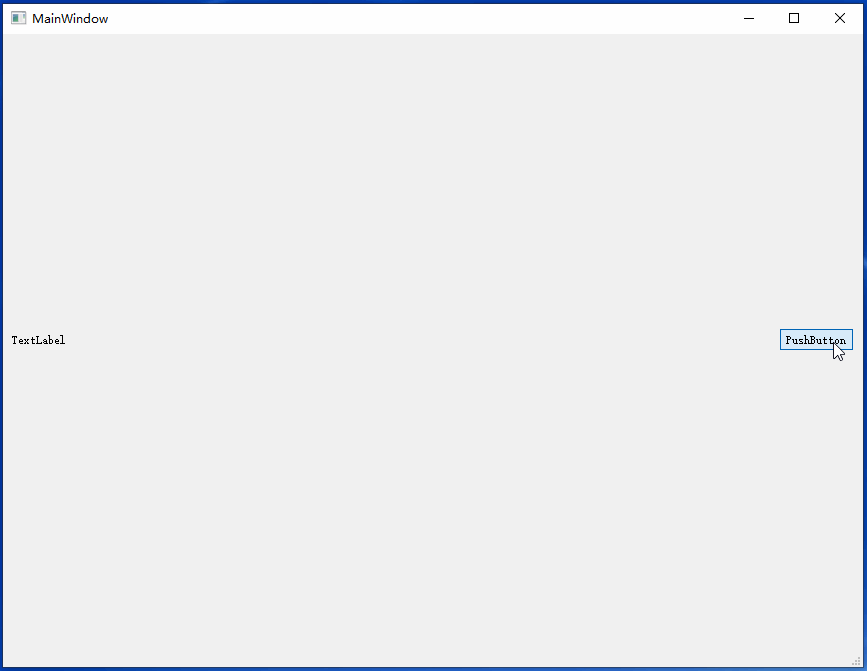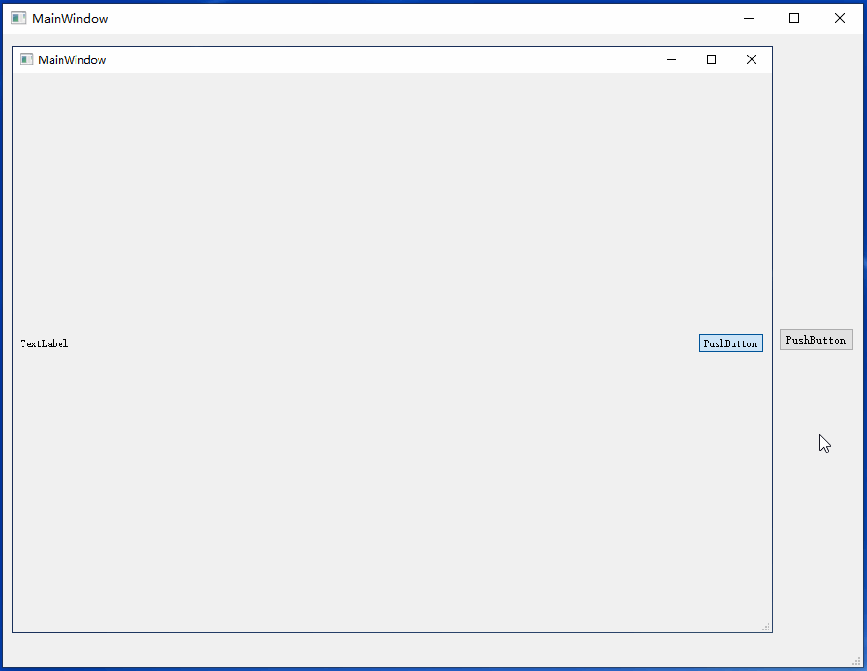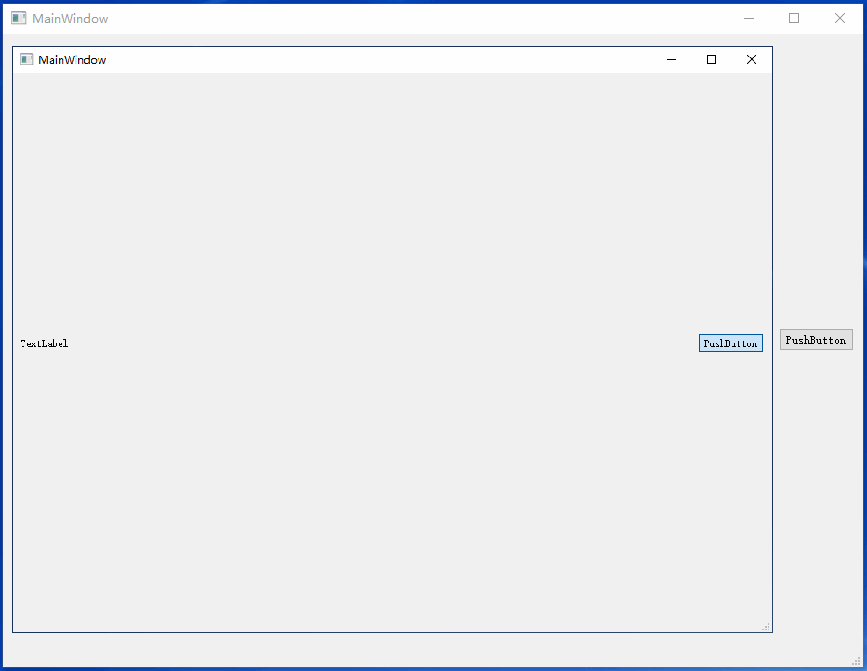
点击按钮抓取窗口自身并显示到QLable中

二.实现

pro文件

QT       += core gui

greaterThan(QT_MAJOR_VERSION, 4): QT += widgets

CONFIG += c++11

SOURCES += \
    main.cpp \
    mainwindow.cpp

HEADERS += \
    mainwindow.h

FORMS += \
    mainwindow.ui

LIBS += -lgdi32 -luser32 -lDwmapi

mainwindow.cpp

#include "mainwindow.h"
#include "ui_mainwindow.h"

#include <Windows.h>
#include <windowsx.h>
#include <Dwmapi.h>
#include <QPixmap>
#include <QImage>
#include <QDebug>

MainWindow::MainWindow(QWidget *parent)
    : QMainWindow(parent)
    , ui(new Ui::MainWindow)
{
    ui->setupUi(this);
}

MainWindow::~MainWindow()
{