题目
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回 true ,否则返回 false 。假设输入的数组的任意两个数字都互不相同。
数据范围: 节点数量 0≤n≤1000 ,节点上的值满足 1≤val≤10^5 ,保证节点上的值各不相同
要求:空间复杂度 O(n) ,时间时间复杂度 O(n2)
提示:
1.二叉搜索树是指父亲节点大于左子树中的全部节点,但是小于右子树中的全部节点的树。
2.该题我们约定空树不是二叉搜索树
3.后序遍历是指按照 “左子树-右子树-根节点” 的顺序遍历
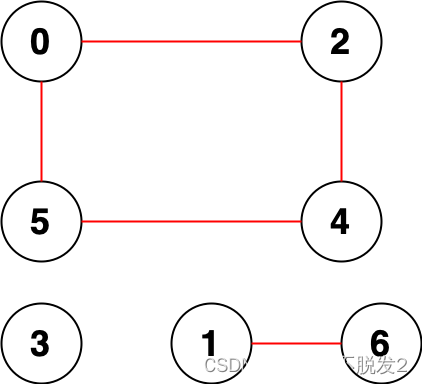
4.参考下面的二叉搜索树,示例 1
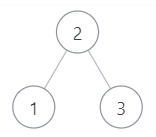
示例1
输入:[1,3,2]
返回值:true
说明:是上图的后序遍历 ,返回true
示例2
输入:[3,1,2]
返回值:false
说明:不属于上图的后序遍历,从另外的二叉搜索树也不能后序遍历出该序列 ,因为最后的2一定是根节点,前面一定是孩子节点,可能是左孩子,右孩子,根节点,也可能是全左孩子,根节点,也可能是全右孩子,根节点,但是[3,1,2]的组合都不能满足这些情况,故返回false
示例3
输入:[5,7,6,9,11,10,8]
返回值:true
解答
源代码
import java.util.*;
public class Solution {
public boolean VerifySquenceOfBST(int [] sequence) {
if (sequence.length == 0) {
return false;
}
return judge(sequence, 0, sequence.length - 1);
}
public boolean judge(int[] sequence, int left, int right) {
if (left >= right) {
return true;
}
int i = 0;
while (i < right && sequence[i] < sequence[right]) {
i++;
}
for (int j = i; j < right; j++) {
if (sequence[j] < sequence[right]) {
return false;
}
}
return judge(sequence, left, i - 1) && judge(sequence, i, right - 1);
}
}总结
设计一个函数,传入一个整数数组和左右边界,判断左右边界之间的序列能否构成一个二叉搜索树的后序遍历序列。
后序遍历序列的最后一个数字一定是根结点,那么从头遍历这个序列,找出连续的小于根结点的数字作为左子树的后序遍历序列,接下来判断余下将要作为右子树的序列中是否小于根结点的数字,若有,则无返回false。之后递归判断左右子树的数组能否构成后序遍历序列,只有两个都返回true时,整个数组才为二叉搜索树的后序遍历序列。