目录
1.AVL树的概念
2.AVL树的模拟实现
AVL树的结构定义
插入
对平衡因子的讨论
旋转
对旋转情况的讨论
1.单旋
1.1左单旋
1.2右单旋
2.双旋
2.1左右双旋
2.2右左双旋
检查是否是AVL树
1.AVL树的概念
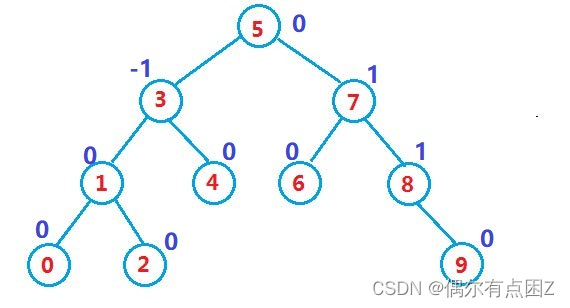
当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
2.AVL树的模拟实现
AVL树的结构定义
节点

AVLTree

插入
插入节点会影响祖先(全部或者部分) ==> 需要更新平衡因子 ==> 讨论是否调整
新增节点的位置进行讨论:
- cur == parent->right parent->bf++
- cur == parent->left parent->bf--
什么决定了是否要继续往上更新爷爷节点, 取决于parent所在的子树高度是否变化? 变了继续更新, 不变则不再更新
- a. parent->bf == 1 || parent->bf == -1 parent所在的子树变了.继续更新, 为什么? ==> 说明插入前parent->bf == 0 , 说明两边高度相等, 现在有一边高1, 说明parent的子一边高一边低, 高度变了.
- b. parent->bf ==2 || parent == -2 -> parent所在的子树不平衡了, 需要处理子树(旋转处理)
- c. parent->bf == 0, parent所在的子树高度不变, 不用继续往上更新, 这一次插入结束. 为什么? ==> 说明插入前parent->bf == 1 or -1 ,说明插入之前一边高一边低, 插入节点填上矮的一边, 它的高度不变.
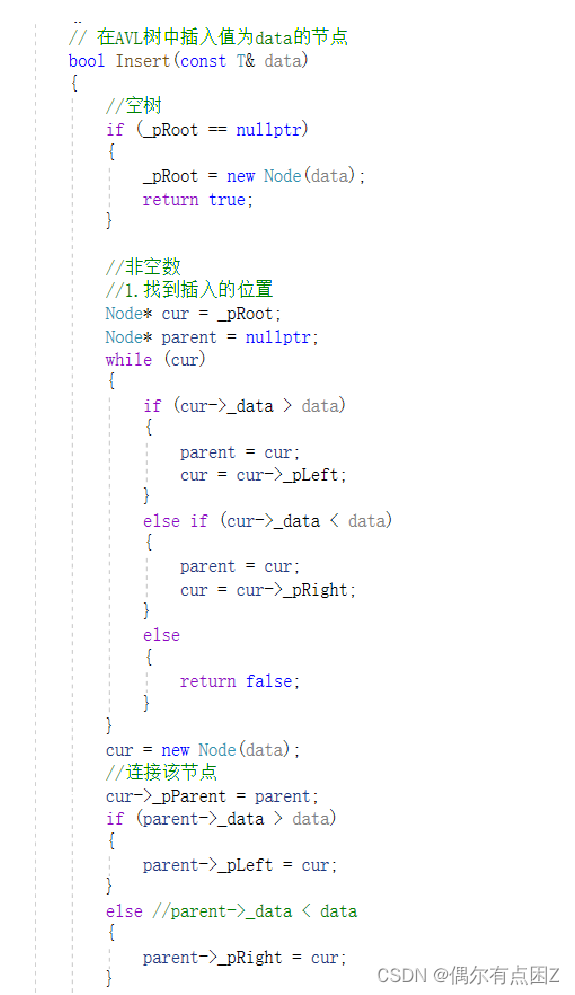
代码(找到插入的位置):
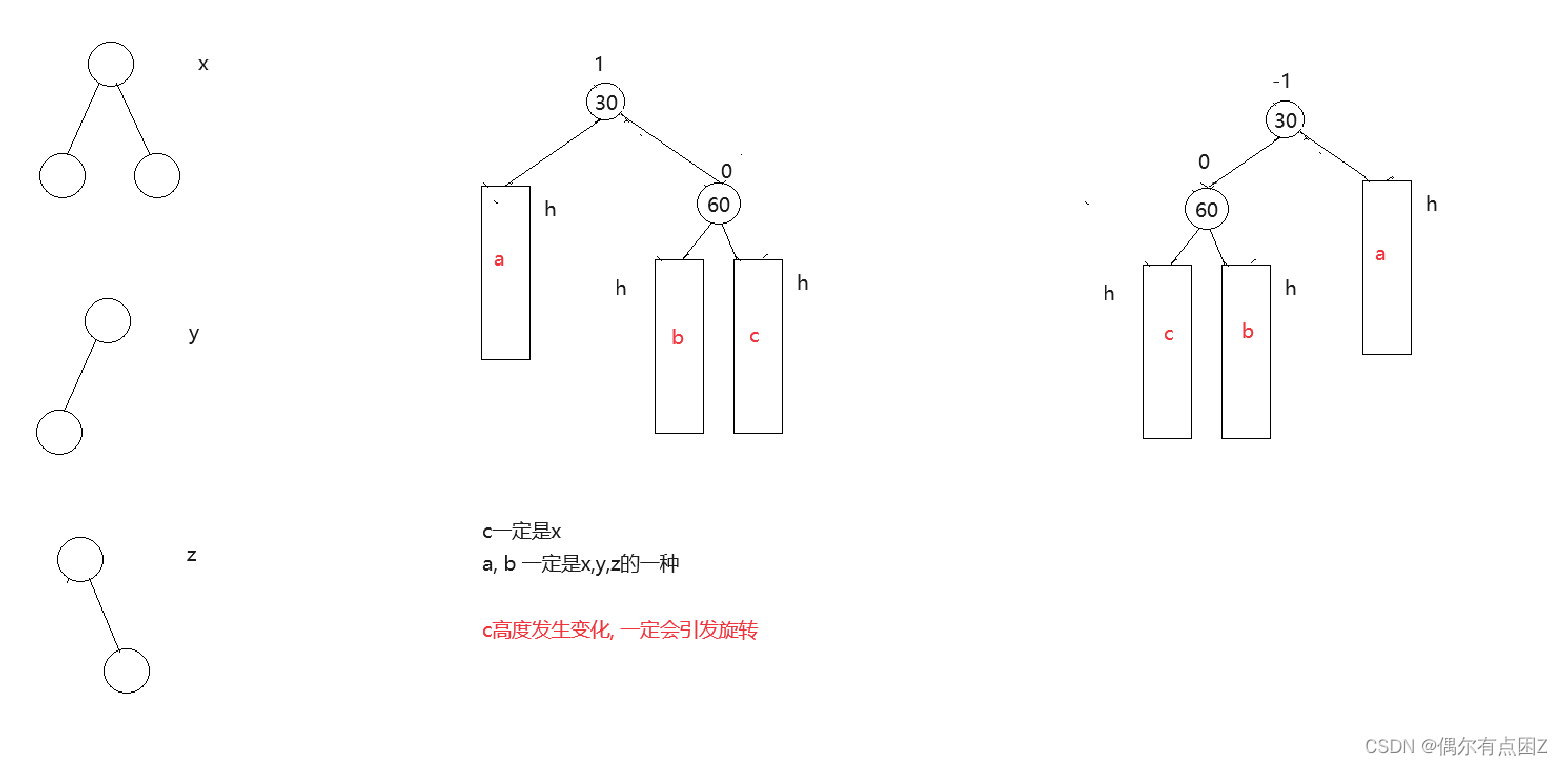
对平衡因子的讨论

旋转
目的: 1.让子树平衡 2. 降低子树的高度
旋转的原则: 保持它继续是搜索树
对旋转情况的讨论
1.单旋
--细节:
--空节点的处理
--parent需要维护(对parent是否是根节点进行讨论) 处理subR/L
--平衡因子更新
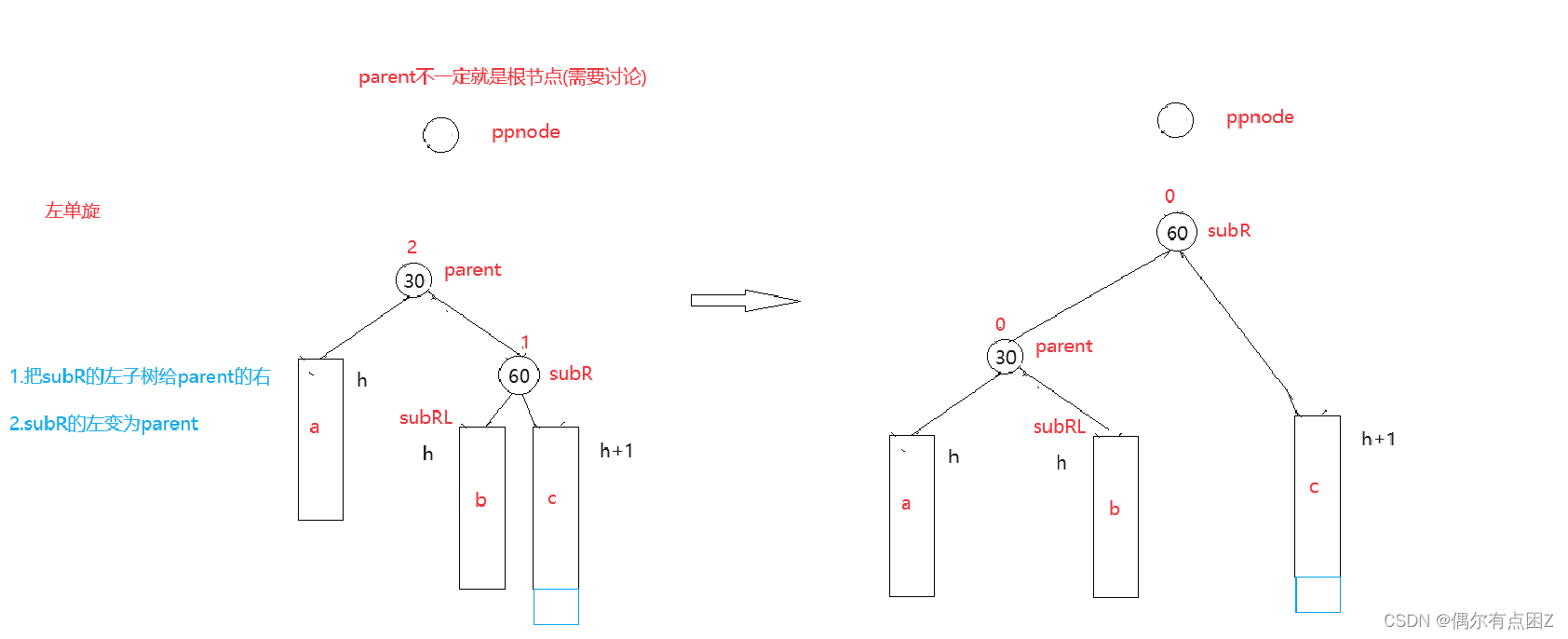
1.1左单旋
parent->_bf == 2 && cur->_bf == 1
--旋转 ==> 处理parent ==>更新平衡因子(parent的parent需要讨论, 影响与subR/L的链接)
代码:
// 左单旋 void RotateL(Node* pParent) { Node* subR = pParent->_pRight; Node* subRL = subR->_pLeft; Node* ppnode = pParent->_pParent; //旋转 //把subR的左(subRL)给parent的右,parent变为subR的左,并处理它们的parent if (subRL) subRL->_pParent = pParent; pParent->_pRight = subRL; pParent->_pParent = subR; subR->_pLeft = pParent; if (pParent == _pRoot) //根节点 { _pRoot = subR; subR->_pParent = nullptr; } else //非根节点 { if (ppnode->_pLeft == pParent) { ppnode->_pLeft = subR; } else //ppnode->_pRight == pParent { ppnode->_pRight == subR; } subR->_pParent = ppnode; } //更新平衡因子 pParent->_bf = subR->_bf = 0; }
1.2右单旋
parent->_bf == -2 && cur->_bf == -1
代码:
// 右单旋 void RotateR(Node* pParent) { Node* subL = pParent->_pLeft; Node* subLR = subL->_pRight; Node* ppnode = pParent->_pParent; //旋转 //把subL的右(subLR)给parent, parent变为subL的右边, 并处理它们的parent if (subLR) subLR->_pParent = pParent; pParent->_pLeft = subLR; pParent->_pParent = subL; subL->_pRight = pParent; if (pParent == _pRoot) { _pRoot = subL; subL->_pParent = nullptr; } else { if (ppnode->_pLeft == pParent) { ppnode->_pLeft = subL; } else { ppnode->_pRight = subL; } subL->_pParent = ppnode; } //更新平衡因子 subL->_bf = pParent->_bf = 0; }
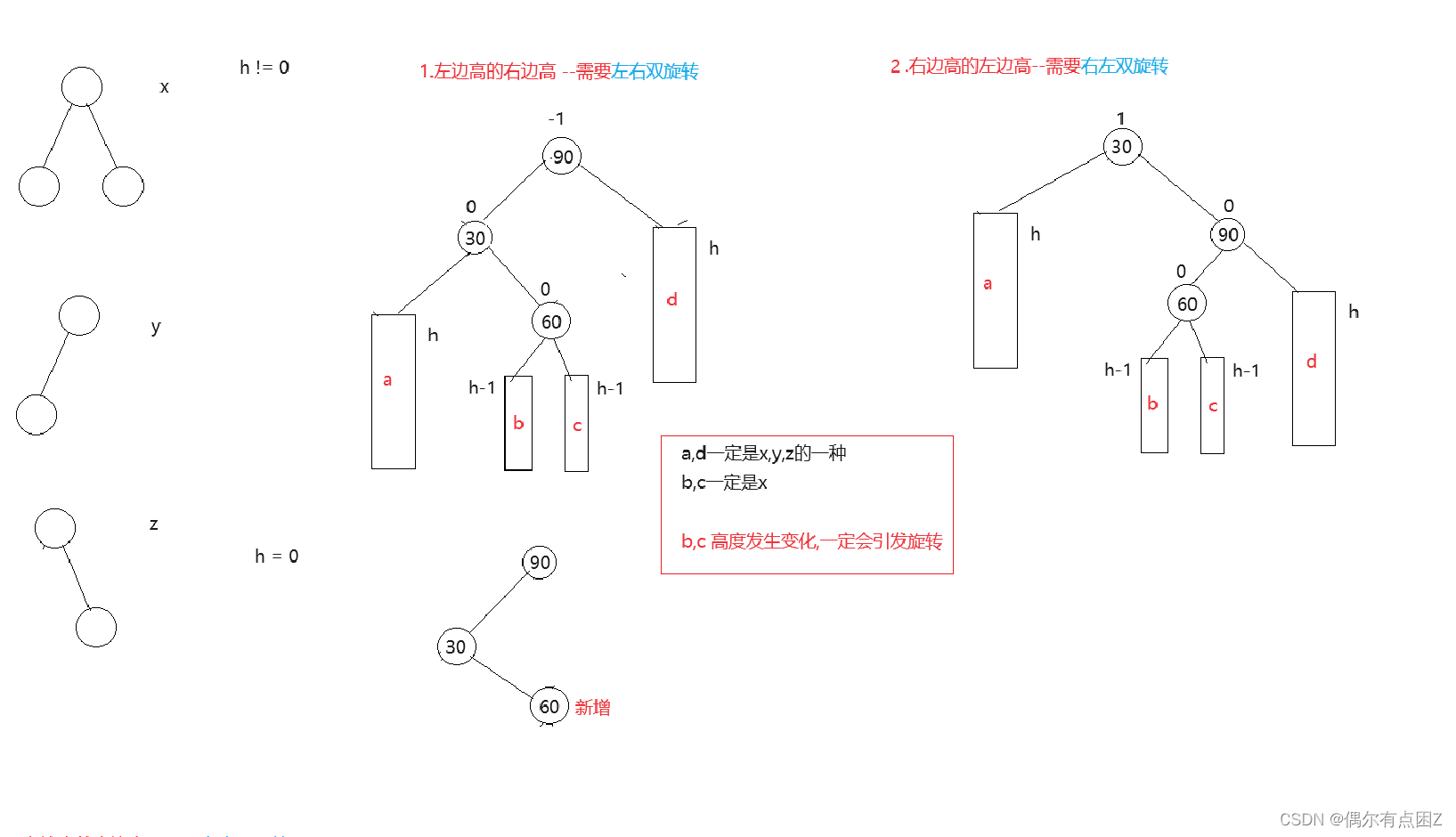
2.双旋
--对单旋的复用 ==> 更新平衡因子
需要保存subRL/LR的平衡因子, 根据插入节点的位置, 进行更新
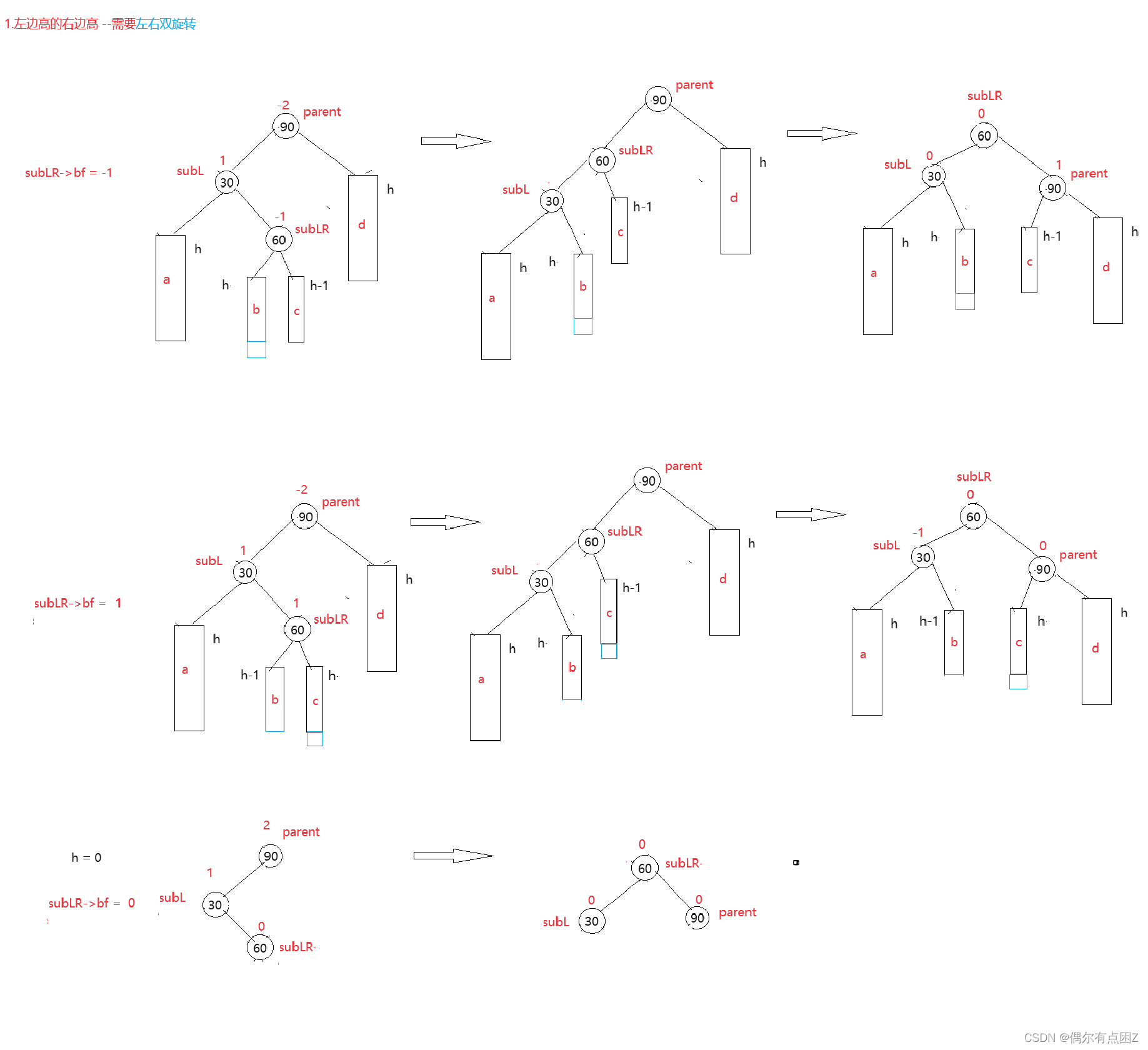
2.1左右双旋
代码:
// 左右双旋 void RotateLR(Node* pParent) { Node* subL = pParent->_pLeft; Node* subLR = subL->_pRight; int bf = subLR->_bf; //旋转 RotateL(pParent->_pLeft); RotateR(pParent); //更新平衡因子 if (bf == -1) { pParent->_bf = 1; subL->_bf = 0; subLR->_bf = 0; } else if (bf == 1) { pParent->_bf = 0; subL->_bf = -1; subLR->_bf = 0; } else if (bf == 0) { pParent->_bf = 0; subL->_bf = 0; subLR->_bf = 0; } else { assert(false); } }
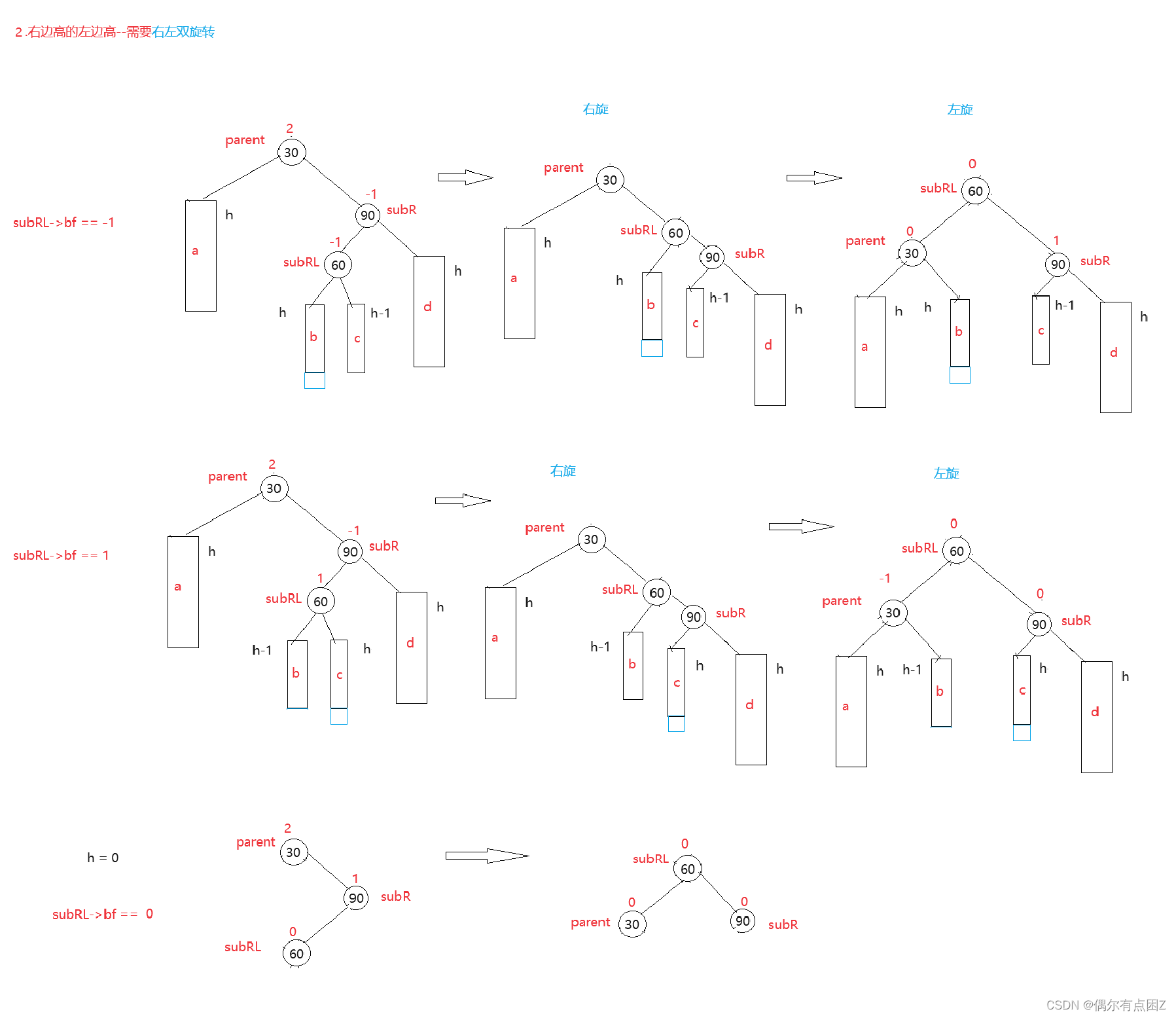
2.2右左双旋
parent -> bf = 2 && cur -> bf = -1
代码:
// 右左双旋 void RotateRL(Node* pParent) { Node* subR = pParent->_pRight; Node* subRL = subR->_pLeft; int bf = subRL->_bf; //右旋 RotateR(pParent->_pRight); RotateL(pParent); //讨论平衡因子的更新 if (bf == -1) { pParent->_bf = 0; subR->_bf = 1; subRL->_bf = 0; } else if (bf == 1) { pParent->_bf = -1; subR->_bf = 0; subRL->_bf = 0; } else if (bf == 0) { pParent->_bf = 0; subR->_bf = 0; subRL->_bf = 0; } else { assert(false); } }
检查是否是AVL树
1.各子树的高度差是否<=1
2.平衡因子是否正确(右子树-左子树高度判断)
代码:
// AVL树的验证 bool IsAVLTree() { return _IsAVLTree(_pRoot); } 根据AVL树的概念验证pRoot是否为有效的AVL树 bool _IsAVLTree(Node* pRoot) { if (pRoot == nullptr) return true; //1.检查各子树的高度差是否小于1 int left_h = _Height(pRoot->_pLeft); int right_h = _Height(pRoot->_pRight); if (right_h - left_h != pRoot->_bf) { cout << "平衡因子异常" << endl; } if (abs(left_h - right_h) > 1) return false; return _IsAVLTree(pRoot->_pLeft) && _IsAVLTree(pRoot->_pRight); } size_t _Height(Node* pRoot) { if (pRoot == nullptr) { return 0; } size_t left_h = _Height(pRoot->_pLeft) + 1; size_t right_h = _Height(pRoot->_pRight) + 1; return left_h > right_h ? left_h : right_h; }
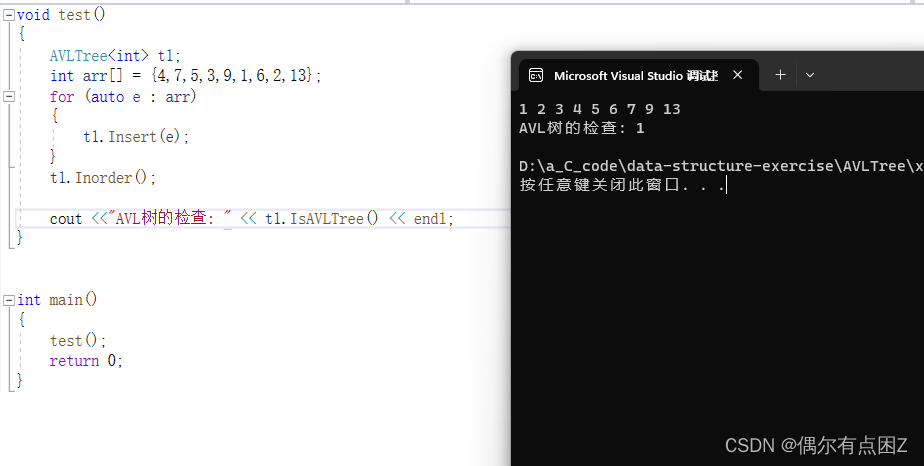
效果:
1.正常情况:
2.屏蔽掉平衡因子的修改: