目录
- 相似度计算
- 基于用户的协同过滤(UserCF)
- 算法评估
- 基于物品的协同过滤(ItemCF)
- 协同过滤算法的权重改进
- 协同过滤算法的问题分析
- 思考
- 学习参考
相似度计算
杰卡德(Jaccard)相似系数
Jaccard 系数是衡量两个集合的相似度一种指标,计算公式如下:
s i m u v = ∣ N ( u ) ∩ N ( v ) ∣ ∣ N ( u ) ∣ ∪ ∣ N ( v ) ∣ sim_{uv}=\frac{|N(u) \cap N(v)|}{|N(u)| \cup|N(v)|} simuv=∣N(u)∣∪∣N(v)∣∣N(u)∩N(v)∣
- 其中 N ( u ) N(u) N(u), N ( v ) N(v) N(v) 分别表示用户 u u u 和用户 v v v 交互物品的集合。
- 对于用户 u u u 和 v v v ,该公式反映了两个交互物品交集的数量占这两个用户交互物品并集的数量的比例。
由于杰卡德相似系数一般无法反映具体用户的评分喜好信息,所以常用来评估用户是否会对某物品进行打分, 而不是预估用户会对某物品打多少分。
余弦相似度
余弦相似度的计算如下,其与杰卡德(Jaccard)相似系数只是在分母上存在差异:
s i m u v = ∣ N ( u ) ∩ N ( v ) ∣ ∣ N ( u ) ∣ ⋅ ∣ N ( v ) ∣ sim_{uv}=\frac{|N(u) \cap N(v)|}{\sqrt{|N(u)|\cdot|N(v)|}} simuv=∣N(u)∣⋅∣N(v)∣∣N(u)∩N(v)∣
余弦相似度衡量了两个向量的夹角,夹角越小越相似。
s i m u v = c o s ( u , v ) = u ⋅ v ∣ u ∣ ⋅ ∣ v ∣ = ∑ i r u i ∗ r v i ∑ i r u i 2 ∑ i r v i 2 sim_{uv} = cos(u,v) =\frac{u\cdot v}{|u|\cdot |v|} = \frac{\sum_i r_{ui}*r_{vi}}{\sqrt{\sum_i r_{ui}^2}\sqrt{\sum_i r_{vi}^2}} simuv=cos(u,v)=∣u∣⋅∣v∣u⋅v=∑irui2∑irvi2∑irui∗rvi
from sklearn.metrics.pairwise import cosine_similarity
i = [1, 0, 0, 0]
j = [1, 0, 1, 0]
cosine_similarity([i, j])

皮尔逊相关系数
相较于余弦相似度,皮尔逊相关系数通过使用用户的平均分对各独立评分进行修正,减小了用户评分偏置的影响。
s i m ( u , v ) = ∑ i ∈ I ( r u i − r ˉ u ) ( r v i − r ˉ v ) ∑ i ∈ I ( r u i − r ˉ u ) 2 ∑ i ∈ I ( r v i − r ˉ v ) 2 sim(u,v)=\frac{\sum_{i\in I}(r_{ui}-\bar r_u)(r_{vi}-\bar r_v)}{\sqrt{\sum_{i\in I }(r_{ui}-\bar r_u)^2}\sqrt{\sum_{i\in I }(r_{vi}-\bar r_v)^2}} sim(u,v)=∑i∈I(rui−rˉu)2∑i∈I(rvi−rˉv)2∑i∈I(rui−rˉu)(rvi−rˉv)
from scipy.stats import pearsonr
i = [1, 0, 0, 0]
j = [1, 0.5, 0.5, 0]
pearsonr(i, j)#返回r值:相关系数[-1,1]之间、、、p值:相关系数显著性
import numpy as np
i = [1, 0, 0, 0]
j = [1, 0.5, 0.5, 0]
np.corrcoef(i, j)
import pandas as pd
data=pd.DataFrame({"i":[1, 0, 0, 0],"j":[1, 0.5, 0.5, 0]})
data.corr("pearson")
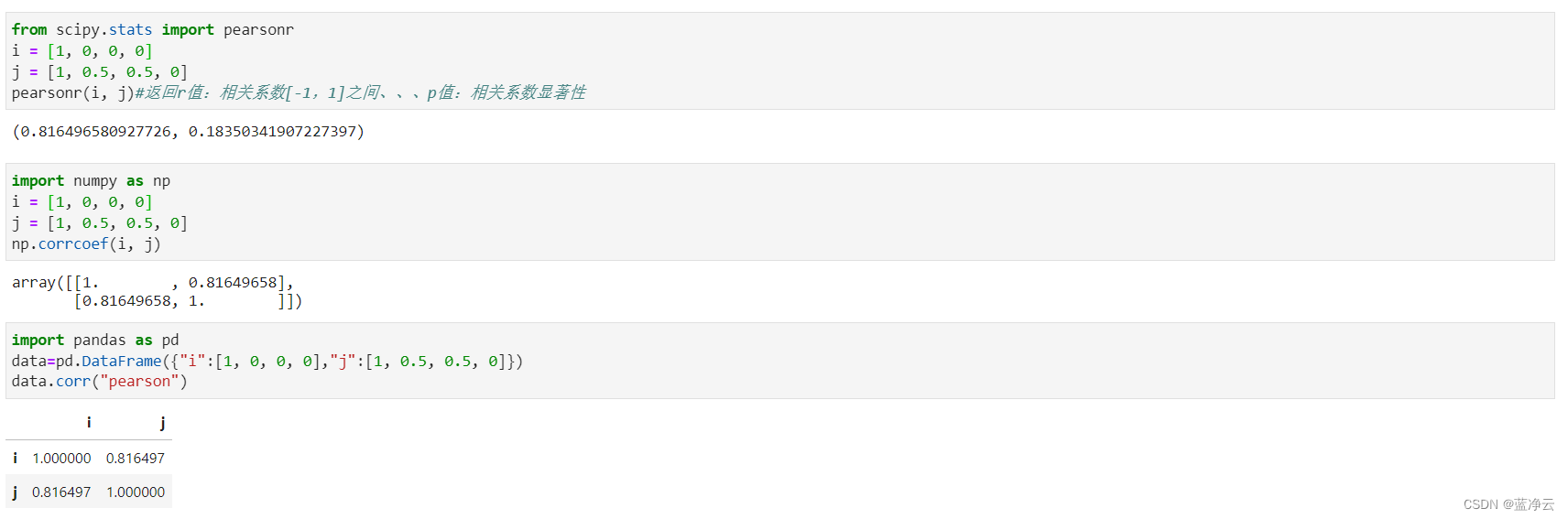
相关性的强度确实是用相关系数的大小来衡量的,但相关大小的评价要以相关系数显著性的评价为前提;
因此,要先检验相关系数的显著性,如果显著,证明相关系数有统计学意义,下一步再来看相关系数大小;
如果相关系数没有统计学意义,那意味着你研究求得的相关系数也许是抽样误差或者测量误差造成的,再进行一次研究结果可 能就大不一样,此时讨论相关性强弱的意义就大大减弱了。
适用场景
- 余弦相似度在度量文本相似度、用户相似度、物品相似度的时候都较为常用。
- 皮尔逊相关度,实际上也是一种余弦相似度。不过先对向量做了中心化,范围在
−
1
-1
−1 到
1
1
1。
- 相关度量的是两个变量的变化趋势是否一致,两个随机变量是不是同增同减。
- 不适合用作计算布尔值向量(0-1)之间相关度。
基于用户的协同过滤(UserCF)
例如,我们要对用户 A 进行物品推荐,可以先找到和他有相似兴趣的其他用户。
然后,将共同兴趣用户喜欢的,但用户 A 未交互过的物品推荐给 A。
给用户推荐物品的过程可以形象化为一个猜测用户对物品进行打分的任务,表格里面是5个用户对于ABCDE 5件物品的一个打分情况,就可以理解为用户对物品的喜欢程度。
| A | B | C | D | E | |
|---|---|---|---|---|---|
| Alice | 5 | 3 | 4 | 4 | ??? |
| user1 | 3 | 1 | 2 | 3 | 5 |
| user2 | 4 | 3 | 4 | 3 | 5 |
| user3 | 3 | 3 | 1 | 5 | 4 |
| user4 | 1 | 5 | 5 | 2 | 1 |
计算过程
-
1、计算用户之间的相似度
我们可以计算出各用户之间的相似程度。对于用户 Alice,选取出与其最相近的 N 个用户。
-
2、计算用户对新物品的评分预测
R A l i c e , E = R ˉ A l i c e + ∑ u s e r ∈ S ( w A l i c e , u s e r ⋅ ( R u s e r , E − R ˉ u s e r ) ) ∑ u s e r ∈ S w A l i c e , u s e r R_{\mathrm{Alice}, \mathrm{E}}=\bar{R}_{Alice} + \frac{\sum_{\mathrm{user} \in S}\left(w_{\mathrm{Alice}, \mathrm{user}} \cdot \left(R_{user, E}-\bar{R}_{user}\right)\right)}{\sum_{\mathrm{user} \in S} w_{\mathrm{Alice}, \mathrm{user}}} RAlice,E=RˉAlice+∑user∈SwAlice,user∑user∈S(wAlice,user⋅(Ruser,E−Rˉuser))
其中, R A l i c e , E R_{Alice,E} RAlice,E 是用户 A l i c e Alice Alice 对物品 E E E 的评分。 R ˉ A l i c e \bar{R}_{Alice} RˉAlice 表示用户 A l i c e Alice Alice 对物品的历史平均评分。权重 w A l i c e , u s e r w_{Alice,user} wAlice,user 是用户 A l i c e Alice Alice 和用户 u s e r user user 的相似度。
-
3、对用户进行物品推荐
在获得用户 Alice 对不同物品的评价预测后, 最终的推荐列表根据预测评分进行排序得到。
建立实验使用的数据表
data = [[5,3,4,4], [3,1,2,3,3], [4,3,4,3,5], [3,3,1,5,4], [1,5,5,2,1]]
index = ['Alice', 'user1', 'user2', 'user3', 'user4']
columns = ['A', 'B', 'C', 'D', 'E']
user_data = pd.DataFrame(data = data, index = index, columns=columns)#.astype(float)
计算用户相似度矩阵
# 计算user1-4皮尔逊相关系数矩阵
u = user_data[1:].values
similarity_matrix = pd.DataFrame(np.corrcoef(u), index=index[1:], columns=index[1:])
# 计算Alice和其他用户相似度
u1 = user_data[user_data.columns[:-1]].values
similarity_matrix1 = pd.DataFrame(np.corrcoef(u2), index=index, columns=index)
similarity_matrix['Alice'] = similarity_matrix1['Alice']
similarity_matrix = similarity_matrix[index]
similarity_matrix.loc['Alice'] = similarity_matrix1.loc['Alice']
similarity_matrix = similarity_matrix.sort_index()[index]
计算与 Alice 最相似的 num 个用户
target_user = 'Alice'
num = 2
sim_users = similarity_matrix[target_user].sort_values(ascending=False)[1:num+1].index.tolist()
预测用户 Alice 对物品 E 的评分
weighted_scores = 0.
corr_values_sum = 0.
target_item = 'E'
for user in sim_users:
weighted_scores = weighted_scores + similarity_matrix[target_user][user] * (user_data[target_item][user] - user_data.loc[user].mean())
corr_values_sum = corr_values_sum + similarity_matrix[target_user][user]
target_user_mean_rating = user_data.loc[target_user].mean()
target_item_pred = target_user_mean_rating + weighted_scores / corr_values_sum
完整代码
import pandas as pd
import numpy as np
# 建立实验使用的数据表
data = [[5,3,4,4], [3,1,2,3,3], [4,3,4,3,5], [3,3,1,5,4], [1,5,5,2,1]]
index = ['Alice', 'user1', 'user2', 'user3', 'user4']
columns = ['A', 'B', 'C', 'D', 'E']
user_data = pd.DataFrame(data = data, index = index, columns=columns)#.astype(float)
print(f'用户对物品的评分表:\n\n{user_data}\n')
# 计算user1-4皮尔逊相关系数矩阵
u = user_data[1:].values
similarity_matrix = pd.DataFrame(np.corrcoef(u), index=index[1:], columns=index[1:])
# 计算Alice和其他用户相似度
u1 = user_data[user_data.columns[:-1]].values
similarity_matrix1 = pd.DataFrame(np.corrcoef(u2), index=index, columns=index)
similarity_matrix['Alice'] = similarity_matrix1['Alice']
similarity_matrix = similarity_matrix[index]
similarity_matrix.loc['Alice'] = similarity_matrix1.loc['Alice']
similarity_matrix = similarity_matrix.sort_index()[index]
print(f'用户相似度矩阵:\n\n{similarity_matrix}\n')
# 计算与 Alice 最相似的 num 个用户
target_user = 'Alice'
num = 2
# 由于最相似的用户为自己,去除本身
sim_users = similarity_matrix[target_user].sort_values(ascending=False)[1:num+1].index.tolist()
print(f'与用户{target_user}最相似的{num}个用户为:{sim_users}\n')
# 预测用户 Alice 对物品 E 的评分
weighted_scores = 0.
corr_values_sum = 0.
target_item = 'E'
for user in sim_users:
weighted_scores = weighted_scores + similarity_matrix[target_user][user] * (user_data[target_item][user] - user_data.loc[user].mean())
corr_values_sum = corr_values_sum + similarity_matrix[target_user][user]
target_user_mean_rating = user_data.loc[target_user].mean()
target_item_pred = target_user_mean_rating + weighted_scores / corr_values_sum
print(f'用户{target_user}对物品{target_item}的预测评分为:{target_item_pred}')
输出
用户对物品的评分表:
A B C D E
Alice 5 3 4 4 NaN
user1 3 1 2 3 3.0
user2 4 3 4 3 5.0
user3 3 3 1 5 4.0
user4 1 5 5 2 1.0
用户相似度矩阵:
Alice user1 user2 user3 user4
Alice 1.000000 0.852803 0.707107 0.000000 -0.792118
user1 0.852803 1.000000 0.467707 0.489956 -0.900149
user2 0.707107 0.467707 1.000000 -0.161165 -0.466569
user3 0.000000 0.489956 -0.161165 1.000000 -0.641503
user4 -0.792118 -0.900149 -0.466569 -0.641503 1.000000
与用户Alice最相似的2个用户为:['user1', 'user2']
用户Alice对物品E的预测评分为:4.871979899370592
算法评估
由于UserCF和ItemCF结果评估部分是共性知识点, 所以在这里统一标识。
召回率
对用户 u u u 推荐 N N N 个物品记为 R ( u ) R(u) R(u), 令用户 u u u 在测试集上喜欢的物品集合为 T ( u ) T(u) T(u), 那么召回率定义为:
Recall = ∑ u ∣ R ( u ) ∩ T ( u ) ∣ ∑ u ∣ T ( u ) ∣ \operatorname{Recall}=\frac{\sum_{u}|R(u) \cap T(u)|}{\sum_{u}|T(u)|} Recall=∑u∣T(u)∣∑u∣R(u)∩T(u)∣
- 含义:在模型召回预测的物品中,预测准确的物品占用户实际喜欢的物品的比例。
精确率
精确率定义为:
Precision = ∑ u ∣ R ( u ) ∩ T ( u ) ∣ ∑ u ∣ R ( u ) ∣ \operatorname{Precision}=\frac{\sum_{u} \mid R(u) \cap T(u)|}{\sum_{u}|R(u)|} Precision=∑u∣R(u)∣∑u∣R(u)∩T(u)∣
- 含义:推荐的物品中,对用户准确推荐的物品占总物品的比例。
- 如要确保召回率高,一般是推荐更多的物品,期望推荐的物品中会涵盖用户喜爱的物品。而实际中,推荐的物品中用户实际喜爱的物品占少数,推荐的精确率就会很低。故同时要确保高召回率和精确率往往是矛盾的,所以实际中需要在二者之间进行权衡。
覆盖率
覆盖率反映了推荐算法发掘长尾的能力, 覆盖率越高, 说明推荐算法越能将长尾中的物品推荐给用户。
Coverage = ∣ ⋃ u ∈ U R ( u ) ∣ ∣ I ∣ \text { Coverage }=\frac{\left|\bigcup_{u \in U} R(u)\right|}{|I|} Coverage =∣I∣ ⋃u∈UR(u)
-
含义:推荐系统能够推荐出来的物品占总物品集合的比例。
- 其中 ∣ I ∣ |I| ∣I∣ 表示所有物品的个数;
- 系统的用户集合为 U U U;
- 推荐系统给每个用户推荐一个长度为 N N N 的物品列表 R ( u ) R(u) R(u).
-
覆盖率表示最终的推荐列表中包含多大比例的物品。如果所有物品都被给推荐给至少一个用户, 那么覆盖率是100%。
新颖度
用推荐列表中物品的平均流行度度量推荐结果的新颖度。 如果推荐出的物品都很热门, 说明推荐的新颖度较低。 由于物品的流行度分布呈长尾分布, 所以为了流行度的平均值更加稳定, 在计算平均流行度时对每个物品的流行度取对数。
- O’scar Celma 在博士论文 "Music Recommendation and Discovery in the Long Tail " 中研究了新颖度的评测。
基于物品的协同过滤(ItemCF)
- 预先根据所有用户的历史行为数据,计算物品之间的相似性。
- 然后,把与用户喜欢的物品相类似的物品推荐给用户。
举例来说,如果用户 1 喜欢物品 A ,而物品 A 和 C 非常相似,则可以将物品 C 推荐给用户1。
ItemCF算法并不利用物品的内容属性计算物品之间的相似度, 主要通过分析用户的行为记录计算物品之间的相似度。
该算法认为, 物品 A 和物品 C 具有很大的相似度是因为喜欢物品 A 的用户极可能喜欢物品 C。
基于物品的协同过滤算法和基于用户的协同过滤算法很像, 所以我们这里直接还是拿上面 Alice 的那个例子来看。
| Alice | user1 | user2 | user3 | user4 | |
|---|---|---|---|---|---|
| A | 5 | 3 | 4 | 3 | 1 |
| B | 3 | 1 | 3 | 3 | 5 |
| C | 4 | 2 | 4 | 1 | 5 |
| D | 4 | 3 | 3 | 5 | 2 |
| E | ??? | 5 | 5 | 4 | 1 |
计算过程
-
1、计算物品之间的相似度(皮尔逊相关系数)
首先计算一下物品E和物品A, B, C, D之间的皮尔逊相关系数。在Alice找出与物品 E 最相近的 n 个物品。
-
2、计算用户对新物品的评分预测
根据 Alice 对最相近的 n 个物品的打分去计算对物品 E 的打分情况。
R A l i c e , E = R ˉ E + ∑ k ∈ I t e m s ( w E , 物品 k ⋅ ( R A l i c e , 物品 k − R ˉ 物品 k ) ) ∑ k ∈ I t e m s w E , 物品 k R_{\mathrm{Alice}, \mathrm{E}}=\bar{R}_{E} + \frac{\sum_{\mathrm{k} \in Items }\left(w_{\mathrm{E}, \mathrm{物品k}} \cdot \left(R_{Alice, 物品k}-\bar{R}_{物品k}\right)\right)}{\sum_{\mathrm{k} \in Items } w_{\mathrm{E}, \mathrm{物品k}}} RAlice,E=RˉE+∑k∈ItemswE,物品k∑k∈Items(wE,物品k⋅(RAlice,物品k−Rˉ物品k))
其中, R A l i c e , E R_{Alice,E} RAlice,E 是用户 A l i c e Alice Alice 对物品 E E E 的评分。 R ˉ E \bar{R}_{E} RˉE 表示用户对物品 E E E 的历史平均评分。权重 w E , 物品 k w_{E,物品k} wE,物品k 是物品 E E E 和物品 k k k 的相似度。
-
3、对用户进行物品推荐
在获得用户 Alice 对不同物品的评价预测后, 最终的推荐列表根据预测评分进行排序得到。
建立实验使用的数据表
data = [[5,3,4,4], [3,1,2,3,3], [4,3,4,3,5], [3,3,1,5,4], [1,5,5,2,1]]
index = ['Alice', 'user1', 'user2', 'user3', 'user4']
columns = ['A', 'B', 'C', 'D', 'E']
user_data = pd.DataFrame(data = data, index = index, columns=columns).T
计算物品相似度矩阵
# 计算物品ABCD皮尔逊相关系数矩阵
u = user_data[:-1].values
similarity_matrix = pd.DataFrame(np.corrcoef(u), index=columns[:-1], columns=columns[:-1])
# 计算物品E与物品ABCD皮尔逊相关系数
u1 = user_data[user_data.columns[1:]].values
similarity_matrix1 = pd.DataFrame(np.corrcoef(u1), index=columns, columns=columns)
similarity_matrix['E'] = similarity_matrix1['E']
similarity_matrix.loc['E'] = similarity_matrix1.loc['E']
计算与 物品E 最相似的 num 个物品
target_user = 'Alice'
target_item = 'E'
num = 2
# 由于最相似的物品为自己,去除本身
sim_items = similarity_matrix[target_item].sort_values(ascending=False)[1:num+1].index.tolist()
预测用户 Alice 对物品 E 的评分
weighted_scores = 0.
corr_values_sum = 0.
for item in sim_items:
weighted_scores = weighted_scores + similarity_matrix[target_item][item] * (user_data[target_user][item] - user_data.loc[item].mean())
corr_values_sum = corr_values_sum + similarity_matrix[target_item][item]
target_user_mean_rating = user_data.loc[target_item].mean()
target_item_pred = target_user_mean_rating + weighted_scores / corr_values_sum
完整代码
import pandas as pd
import numpy as np
# 建立实验使用的数据表
data = [[5,3,4,4], [3,1,2,3,3], [4,3,4,3,5], [3,3,1,5,4], [1,5,5,2,1]]
index = ['Alice', 'user1', 'user2', 'user3', 'user4']
columns = ['A', 'B', 'C', 'D', 'E']
user_data = pd.DataFrame(data = data, index = index, columns=columns).T
print(f'用户对物品的评分表:\n\n{user_data}\n')
# 计算物品ABCD皮尔逊相关系数矩阵
u = user_data[:-1].values
similarity_matrix = pd.DataFrame(np.corrcoef(u), index=columns[:-1], columns=columns[:-1])
# 计算物品E与物品ABCD皮尔逊相关系数
u1 = user_data[user_data.columns[1:]].values
similarity_matrix1 = pd.DataFrame(np.corrcoef(u1), index=columns, columns=columns)
similarity_matrix['E'] = similarity_matrix1['E']
similarity_matrix.loc['E'] = similarity_matrix1.loc['E']
print(f'物品相似度矩阵:\n\n{similarity_matrix}\n')
# 计算与 物品E 最相似的 num 个物品
target_user = 'Alice'
target_item = 'E'
num = 2
# 由于最相似的物品为自己,去除本身
sim_items = similarity_matrix[target_item].sort_values(ascending=False)[1:num+1].index.tolist()
print(f'与物品{target_item}最相似的{num}个物品为:{sim_items}\n')
# 预测用户 Alice 对物品 E 的评分
weighted_scores = 0.
corr_values_sum = 0.
for item in sim_items:
weighted_scores = weighted_scores + similarity_matrix[target_item][item] * (user_data[target_user][item] - user_data.loc[item].mean())
corr_values_sum = corr_values_sum + similarity_matrix[target_item][item]
target_user_mean_rating = user_data.loc[target_item].mean()
target_item_pred = target_user_mean_rating + weighted_scores / corr_values_sum
print(f'用户{target_user}对物品{target_item}的预测评分为:{target_item_pred}')
输出
用户对物品的评分表:
Alice user1 user2 user3 user4
A 5.0 3.0 4.0 3.0 1.0
B 3.0 1.0 3.0 3.0 5.0
C 4.0 2.0 4.0 1.0 5.0
D 4.0 3.0 3.0 5.0 2.0
E NaN 3.0 5.0 4.0 1.0
物品相似度矩阵:
A B C D E
A 1.000000 -0.476731 -0.123091 0.532181 0.969458
B -0.476731 1.000000 0.645497 -0.310087 -0.478091
C -0.123091 0.645497 1.000000 -0.720577 -0.427618
D 0.532181 -0.310087 -0.720577 1.000000 0.581675
E 0.969458 -0.478091 -0.427618 0.581675 1.000000
与物品E最相似的2个物品为:['A', 'D']
用户Alice对物品E的预测评分为:4.6
协同过滤算法的权重改进
-
base 公式
w i j = ∣ N ( i ) ⋂ N ( j ) ∣ ∣ N ( i ) ∣ w_{i j}=\frac{|N(i) \bigcap N(j)|}{|N(i)|} wij=∣N(i)∣∣N(i)⋂N(j)∣
- 该公式表示同时喜好物品 i i i 和物品 j j j 的用户数,占喜爱物品 i i i 的比例。
- 缺点:若物品 j j j 为热门物品,那么它与任何物品的相似度都很高。
-
对热门物品进行惩罚
w i j = ∣ N ( i ) ∩ N ( j ) ∣ ∣ N ( i ) ∣ ∣ N ( j ) ∣ w_{i j}=\frac{|N(i) \cap N(j)|}{\sqrt{|N(i)||N(j)|}} wij=∣N(i)∣∣N(j)∣∣N(i)∩N(j)∣
- 根据 base 公式在的问题,对物品 j j j 进行打压。打压的出发点很简单,就是在分母再除以一个物品 j j j 被购买的数量。
- 此时,若物品 j j j 为热门物品,那么对应的 N ( j ) N(j) N(j) 也会很大,受到的惩罚更多。
-
控制对热门物品的惩罚力度
w i j = ∣ N ( i ) ∩ N ( j ) ∣ ∣ N ( i ) ∣ 1 − α ∣ N ( j ) ∣ α w_{i j}=\frac{|N(i) \cap N(j)|}{|N(i)|^{1-\alpha}|N(j)|^{\alpha}} wij=∣N(i)∣1−α∣N(j)∣α∣N(i)∩N(j)∣
- 除了第二点提到的办法,在计算物品之间相似度时可以对热门物品进行惩罚外。
- 可以在此基础上,进一步引入参数 α \alpha α ,这样可以通过控制参数 α \alpha α来决定对热门物品的惩罚力度。
-
对活跃用户的惩罚
- 在计算物品之间的相似度时,可以进一步将用户的活跃度考虑进来。
w i j = ∑ u∈N(i)∩N(j) 1 log 1 + ∣ N ( u ) ∣ ∣ N ( i ) ∣ 1 − α ∣ N ( j ) ∣ α w_{i j}=\frac{\sum_{\operatorname{\text {u}\in N(i) \cap N(j)}} \frac{1}{\log 1+|N(u)|}}{|N(i)|^{1-\alpha}|N(j)|^{\alpha}} wij=∣N(i)∣1−α∣N(j)∣α∑u∈N(i)∩N(j)log1+∣N(u)∣1
- 对于异常活跃的用户,在计算物品之间的相似度时,他的贡献应该小于非活跃用户。
- 在计算物品之间的相似度时,可以进一步将用户的活跃度考虑进来。
协同过滤算法的问题分析
协同过滤算法存在的问题之一就是泛化能力弱:
- 即协同过滤无法将两个物品相似的信息推广到其他物品的相似性上。
- 导致的问题是热门物品具有很强的头部效应, 容易跟大量物品产生相似, 而尾部物品由于特征向量稀疏, 导致很少被推荐。
比如下面这个例子:
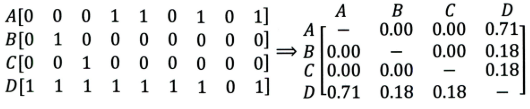
- 左边矩阵中, A , B , C , D A, B, C, D A,B,C,D 表示的是物品。
- 可以看出, D D D 是一件热门物品,其与 A 、 B 、 C A、B、C A、B、C 的相似度比较大。因此,推荐系统更可能将 D D D 推荐给用过 A 、 B 、 C A、B、C A、B、C 的用户。
- 但是,推荐系统无法找出 A , B , C A,B,C A,B,C 之间相似性的原因是交互数据太稀疏, 缺乏相似性计算的直接数据。
所以这就是协同过滤的天然缺陷:推荐系统头部效应明显, 处理稀疏向量的能力弱。
为了解决这个问题, 同时增加模型的泛化能力。2006年,矩阵分解技术(Matrix Factorization, MF)被提出:
- 该方法在协同过滤共现矩阵的基础上, 使用更稠密的隐向量表示用户和物品, 挖掘用户和物品的隐含兴趣和隐含特征。
- 在一定程度上弥补协同过滤模型处理稀疏矩阵能力不足的问题。
思考
- 什么时候使用UserCF,什么时候使用ItemCF?为什么?
(1)UserCF
由于是基于用户相似度进行推荐, 所以具备更强的社交特性, 这样的特点非常适于用户少, 物品多, 时效性较强的场合。
- 比如新闻推荐场景, 因为新闻本身兴趣点分散, 相比用户对不同新闻的兴趣偏好, 新闻的及时性,热点性往往更加重要, 所以正好适用于发现热点,跟踪热点的趋势。
- 另外还具有推荐新信息的能力, 更有可能发现惊喜, 因为看的是人与人的相似性, 推出来的结果可能更有惊喜,可以发现用户潜在但自己尚未察觉的兴趣爱好。
(2)ItemCF
- 这个更适用于兴趣变化较为稳定的应用, 更接近于个性化的推荐, 适合物品少,用户多,用户兴趣固定持久, 物品更新速度不是太快的场合。
- 比如推荐艺术品, 音乐, 电影。
2.上面介绍的相似度计算方法有什么优劣之处?
cosine相似度计算简单方便,一般较为常用。但是,当用户的评分数据存在 bias 时,效果往往不那么好。
- 简而言之,就是不同用户评分的偏向不同。部分用户可能乐于给予好评,而部分用户习惯给予差评或者乱评分。
- 这个时候,根据cosine 相似度计算出来的推荐结果效果会打折扣。
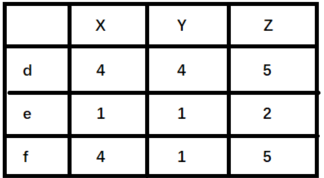
举例来说明,如下图(
X,Y,Z表示物品,d,e,f表示用户):
- 如果使用余弦相似度进行计算,用户 d 和 e 之间较为相似。但是实际上,用户 d 和 f 之间应该更加相似。只不过由于 d 倾向于打高分,e 倾向于打低分导致二者之间的余弦相似度更高。
- 这种情况下,可以考虑使用皮尔逊相关系数计算用户之间的相似性关系。
3.协同过滤还存在其他什么缺陷?有什么比较好的思路可以解决(缓解)?
- 协同过滤的优点就是没有使用更多的用户或者物品属性信息,仅利用用户和物品之间的交互信息就能完成推荐,该算法简单高效。
- 但这也是协同过滤算法的一个弊端。由于未使用更丰富的用户和物品特征信息,这也导致协同过滤算法的模型表达能力有限。
- 对于该问题,逻辑回归模型(LR)可以更好地在推荐模型中引入更多特征信息,提高模型的表达能力。