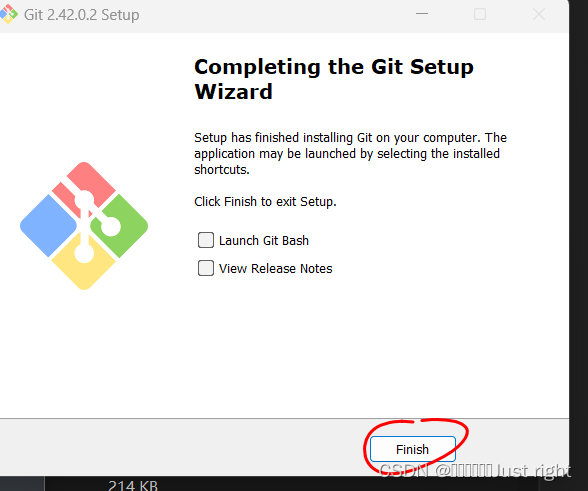
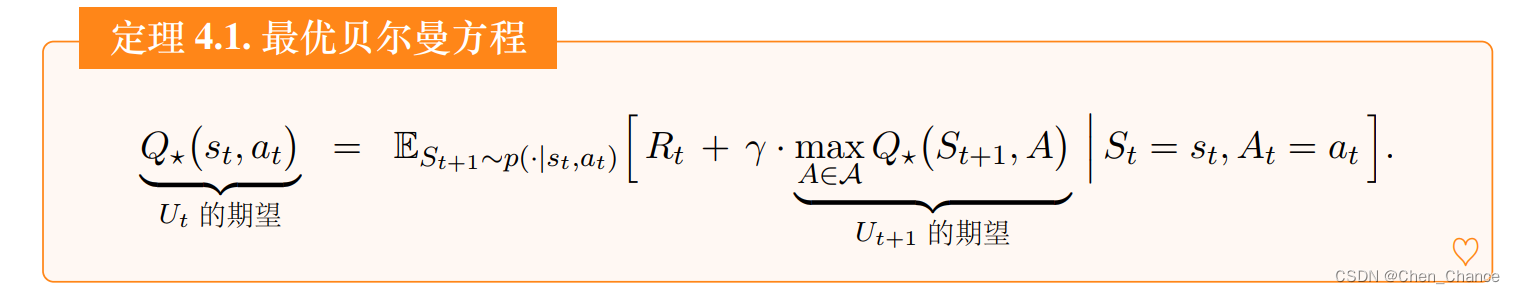4.1 DQN

- 最优动作价值函数的用途
假如我们知道 Q ⋆ Q_⋆ Q⋆,我们就能用它做控制。
我们希望知道 Q ⋆ Q_⋆ Q⋆,因为它就像是先知一般,可以预见未来,在 t 时刻就预见 t 到 n时刻之间的累计奖励的期望。假如我们有 Q ⋆ Q_⋆ Q⋆ 这位先知,我们就遵照先知的指导,最大化未来的累计奖励。然而在实践中我们不知道 Q ⋆ Q_⋆ Q⋆ 的函数表达式。是否有可能近似出 Q ⋆ Q_⋆ Q⋆这位先知呢?
对于超级玛丽这样的游戏,学出来一个“先知”并不难。假如让我们重复玩超级玛丽一亿次,那我们就会像先知一样,看到当前状态,就能准确判断出当前最优的动作是什么。这说明只要有足够多的“经验”,就能训练出超级玛丽中的“先知”。
- 最优动作价值函数的近似


- DQN 的梯度

4.2 时间差分(TD)算法
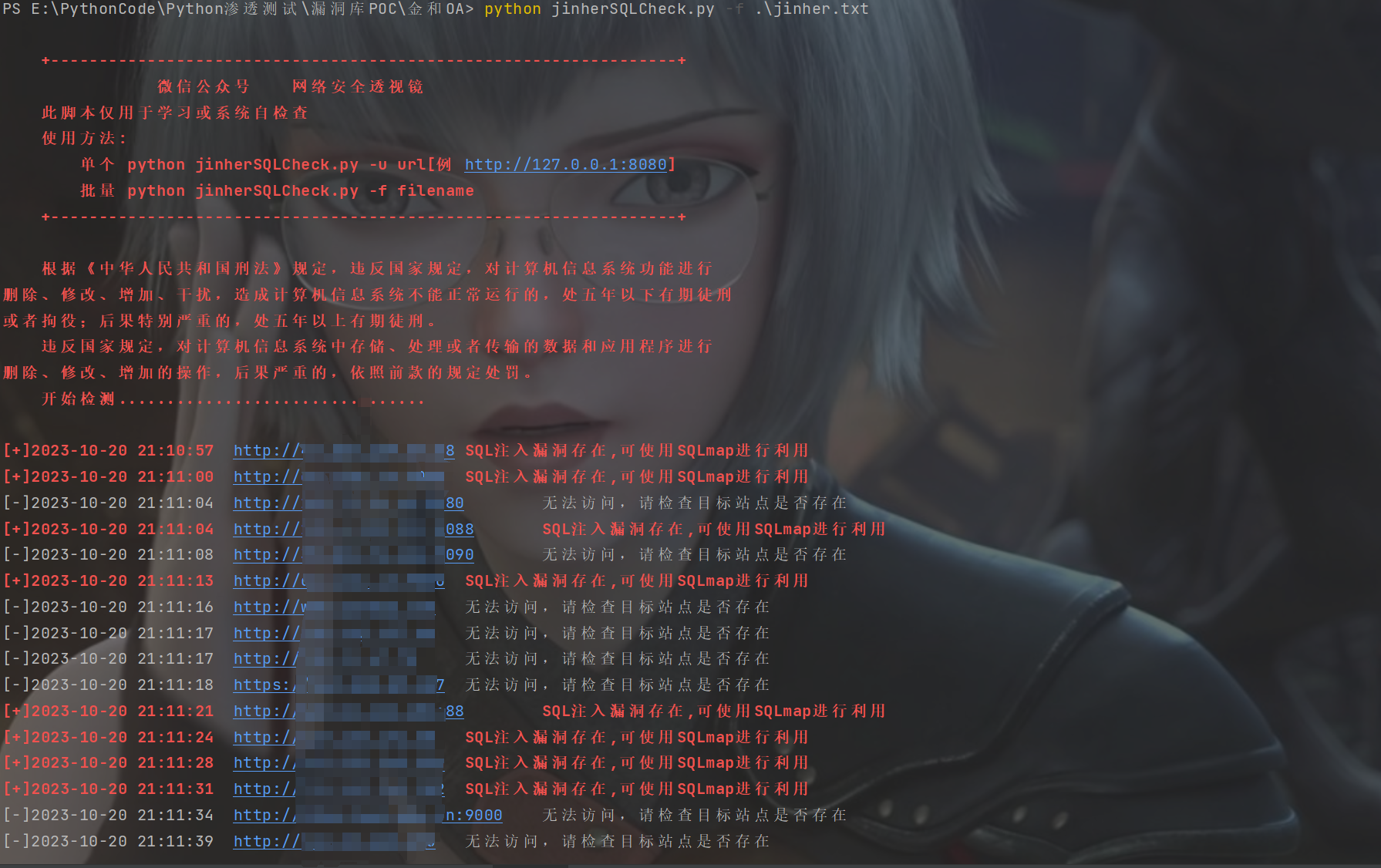
训练 DQN 最常用的算法是时间差分(temporal difference,缩写 TD)。 TD 算法不太好理解,所以本节举一个通俗易懂的例子讲解 TD 算法。
4.2.1 驾车时间预测的例子
假设我们有一个模型 Q ( s , d ; w ) Q(s, d; w) Q(s,d;w),其中 s s s 是起点, d d d 是终点, w w w 是参数。模型 Q 可以预测开车出行的时间开销。这个模型一开始不准确,甚至是纯随机的。但是随着很多人用这个模型,得到更多数据、更多训练,这个模型就会越来越准,会像谷歌地图一样准。
我们该如何训练这个模型呢?在用户出发前,用户告诉模型起点 s s s 和终点 d d d,模型做一个预测 q ^ = Q ( s , d ; w ) \hat q = Q(s, d; w) q^=Q(s,d;w)。当用户结束行程的时候,把实际驾车时间 y y y 反馈给模型。两者之差 q ^ − y \hat q− y q^−y 反映出模型是高估还是低估了驾驶时间,以此来修正模型,使得模型的估计更准确。
4.2.2 TD 算法
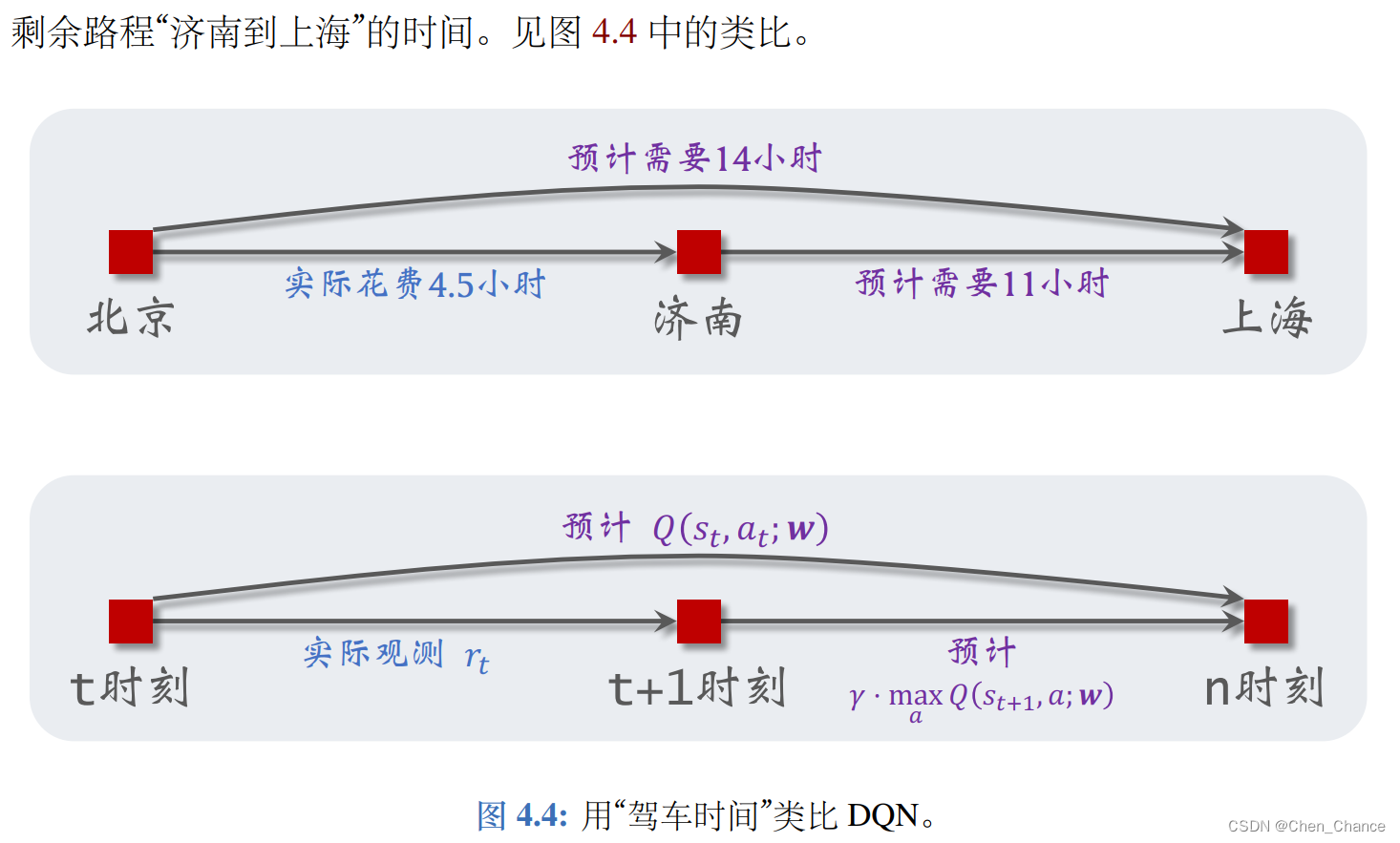
接着上文驾车时间的例子。出发前模型估计全程时间为
q
^
=
14
小时
\hat q = 14 小时
q^=14小时;模型建议的路线会途径济南。我从北京出发,过了
r
=
4.5
小时
r = 4.5 小时
r=4.5小时,我到达济南。此时我再让模型做一次预测,模型告诉我
q
^
′
≜
Q
(
“济南”
,
“上海”
;
w
)
=
11
\hat q^{'} ≜ Q(“济南”, “上海”; w)=11
q^′≜Q(“济南”,“上海”;w)=11





4.3 用TD训练DQN
注意,本节推导出的是最原始的TD 算法,在实践中效果不佳。实际训练 DQN 的时候,应当使用第 6 章介绍的高级技巧。
4.3.1 算法推导