题目
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例 1:
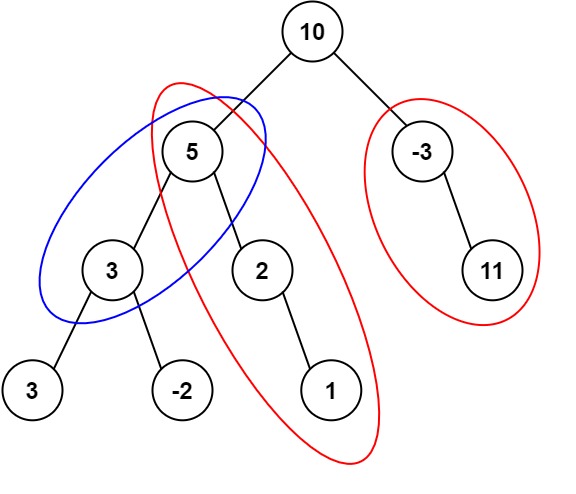
输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出:3 解释:和等于 8 的路径有 3 条,如图所示。
示例 2:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:3
提示:
- 二叉树的节点个数的范围是
[0,1000] -109 <= Node.val <= 109-1000 <= targetSum <= 1000
注意:本题与主站 437 题相同:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
LCR 050. 路径总和 III - 力扣(LeetCode)
题解
思路一:暴力解法,枚举每个结点作为根,在对枚举的每颗子树进行dfs(即两次dfs),判断是否存在targetSum。 注意:过程sum可能会溢出,故设为long。
代码:
class Solution {
long target;
int ans = 0;
public void dfs(TreeNode t, long sum) {
if (t == null) return;
if (sum + t.val == target)
ans++;
dfs(t.left, sum + t.val);
dfs(t.right, sum + t.val);
}
public void dfs1(TreeNode t){
if(t == null) return;
dfs(t, 0);
dfs1(t.left);
dfs1(t.right);
}
public int pathSum(TreeNode root, int targetSum) {
this.target = targetSum;
dfs1(root);
return ans;
}
}思路二:前缀和思想。每次到一个新的结点,总是会重复计算结点间的路径和,于是可以使用一个map<从根节点到当前结点的路径长度,有多少条该路径>,来记录路径sum,然后当前sum-之前的sum==target的,即是一条路径。
有两个点需要注意:1.根节点为空路径,map要添加<0,1>。
2.每个子树操作完之后,要消除该子树对其他子树的影响,即map的value值是会减少的。
代码:
class Solution {
//map<从根节点到当前结点的路径长度,有多少条该路径>
Map<Long, Integer> sumCountMap = new HashMap<Long, Integer>();
public int pathSum(TreeNode root, int targetSum) {
if (root == null) return 0;
sumCountMap.put(0L, 1);//起点的空路径
return getCounts(root, root.val, targetSum);
}
public int getCounts(TreeNode node, long sum, int targetSum) {
//递归的每个子树里都有一个新的count加进来。
int count = sumCountMap.getOrDefault(sum - targetSum, 0);
sumCountMap.put(sum, sumCountMap.getOrDefault(sum, 0) + 1);
if (node.left != null)
count += getCounts(node.left, sum + node.left.val, targetSum);
if (node.right != null)
count += getCounts(node.right, sum + node.right.val, targetSum);
//从子树里退出去的时候,消除当前的sum数量对其他子树的影响
sumCountMap.put(sum, sumCountMap.get(sum) - 1);
return count;
}
}