前言

1、组合
2、组合总和|||
3、电话号码的字母组合

一、组合（力扣77）

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按任何顺序返回答案。
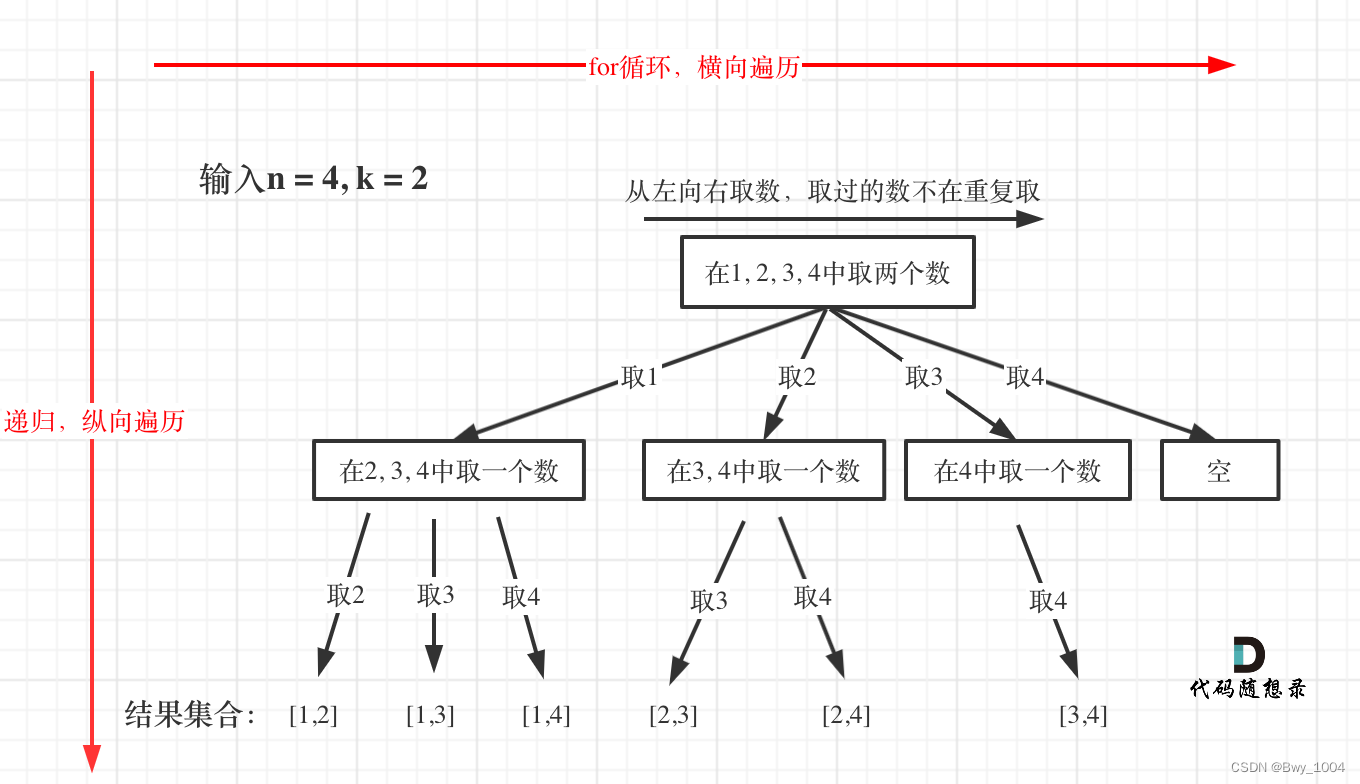
在这里插入图片描述

图中可以发现n相当于树的宽度，k相当于树的深度。
图中每次搜索到了叶子节点，我们就找到了一个结果。

startIndex 就是防止出现重复的组合。
startIndex来记录下一层递归，搜索的起始位置。

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> paths = new LinkedList<>();
    public List<List<Integer>> combine(int n, int k) {
        backtracking(n,k,1);
        return res;
    }
    public void backtracking(int n,int k,int startIndex){

        if(paths.size()==k){ //收集结果
            res.add(new ArrayList<>(paths));
            return ;
        }
        for(int i = startIndex;i<=n;i++){
            paths.add(i);
            backtracking(n,k,i+1);
            paths.removeLast(i); //回溯
        }
    }
}

剪枝优化

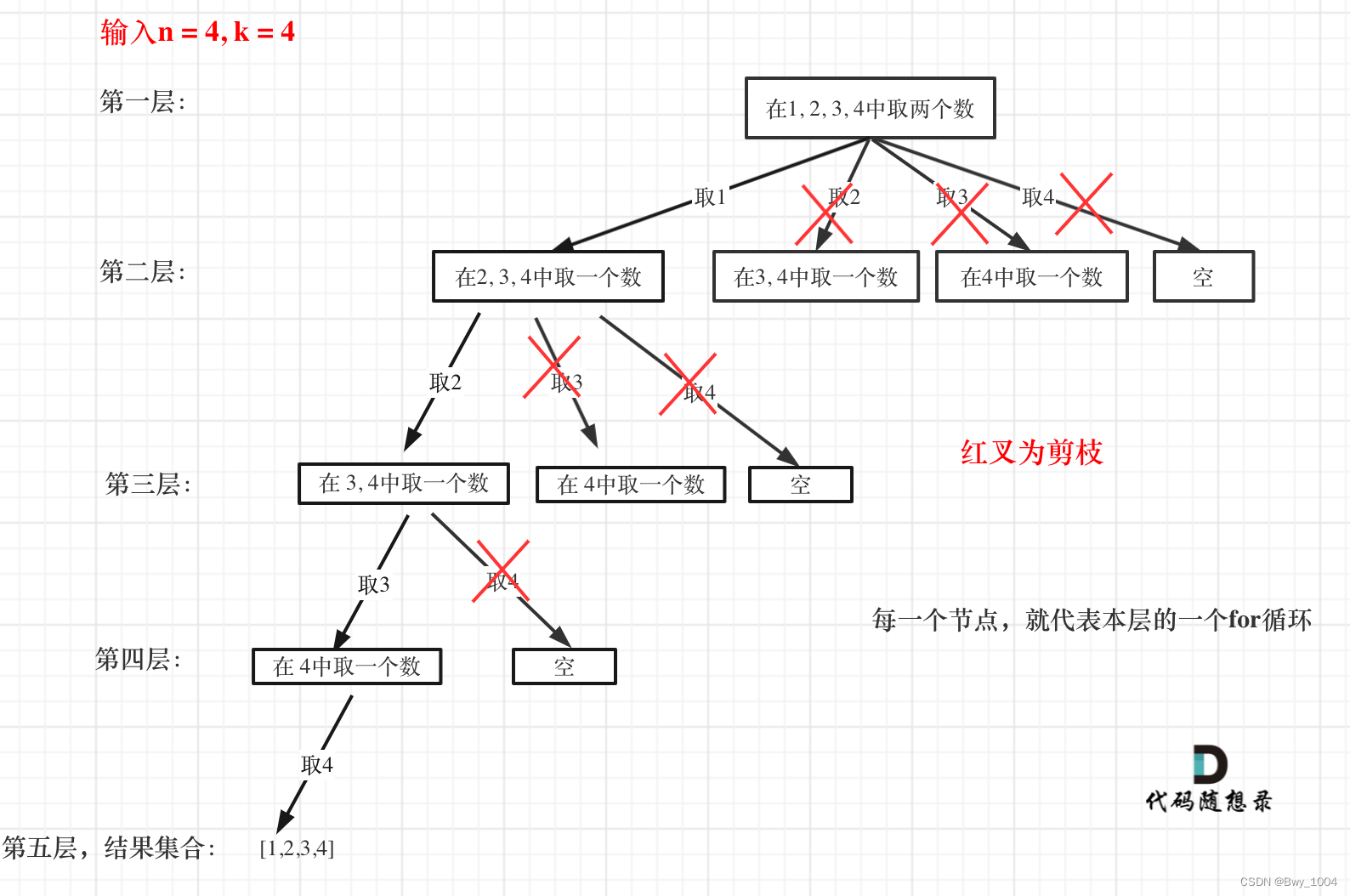
在这里插入图片描述
优化过程如下：

1、已经选择的元素个数：path.size();

2、还需要的元素个数为: k - path.size();

3、在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。

举个例子，n = 4，k = 4，目前已经选取的元素为0（path.size为0），n - (k - 0) + 1 即 4 - ( 4 - 0) + 1 = 1。

从1开始搜索都是合理的，可以是组合[1, 2, 3, 4]

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> paths = new LinkedList<>();
    public List<List<Integer>> combine(int n, int k) {
        backtracking(n,k,1);
        return res;
    }
    public void backtracking(int n,int k,int startIndex){

        if(paths.size()==k){ //收集结果
            res.add(new ArrayList<>(paths));
            return ;
        }
        for(int i = startIndex;i<=n-(k-paths.size())+1;i++){
            paths.add(i);
            backtracking(n,k,i+1);
            paths.removeLast(); //回溯
        }
    }
}

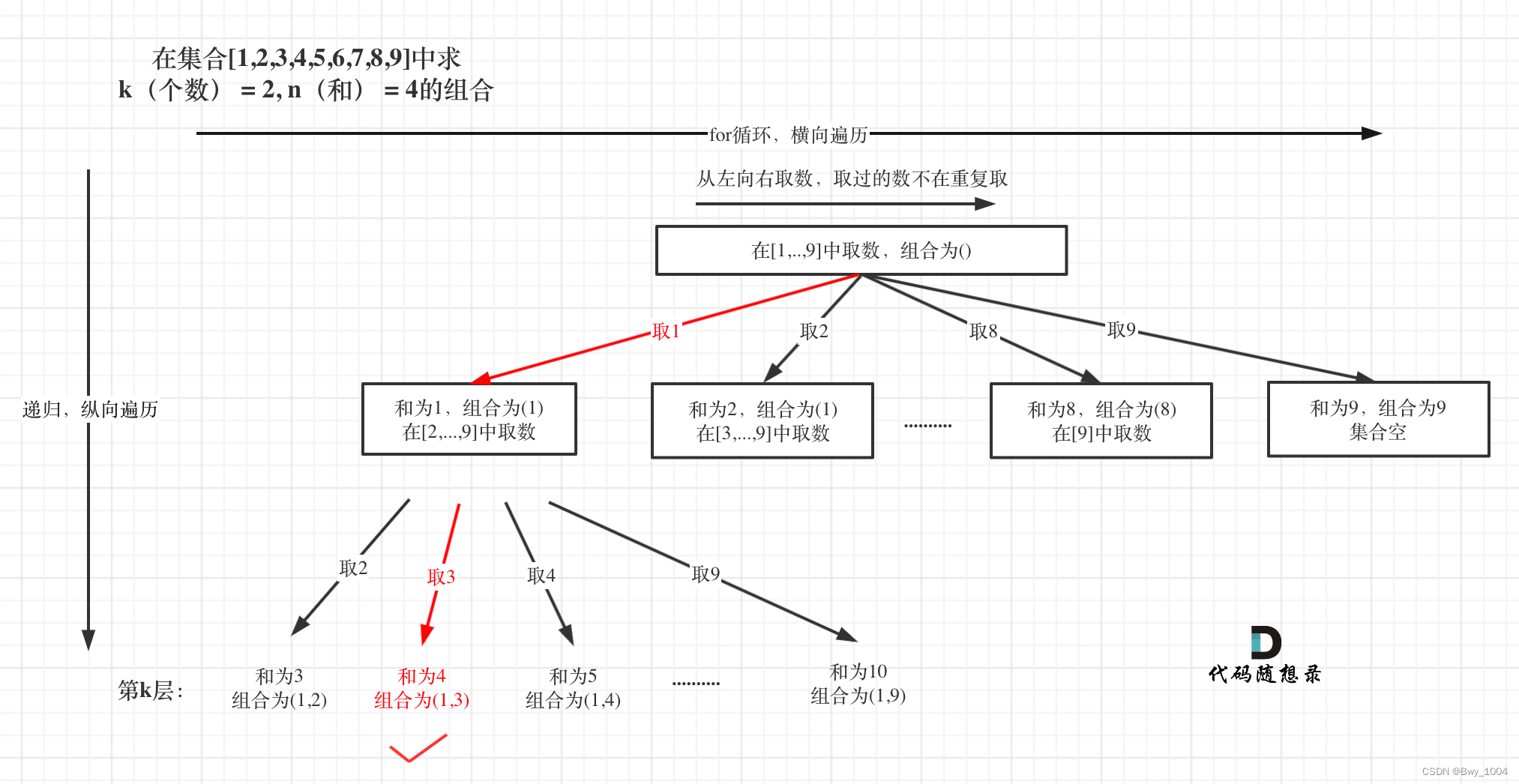
在这里插入图片描述

二、组合总和 III（力扣216）

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

只使用数字1到9
每个数字最多使用一次
返回所有可能的有效组合的列表。该列表不能包含相同的组合两次，组合可以以任何顺序返回。
在这里插入图片描述

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> paths = new LinkedList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
        int[] nums = new int[9];
        for(int i=0;i<nums.length;i++){
            nums[i]=i+1;
        }
        backtracking(k,n,0,nums);
        return res;
    }

    public void backtracking(int k,int n,int startIndex,int[] nums){
        int sum=0;
        if(paths.size() == k){
            for(int i=0;i<paths.size();i++){
                sum += paths.get(i);
            }
            if(sum==n){
                //收集结果
                res.add(new ArrayList<>(paths));
                return ;
            }
        }

        for(int i = startIndex;i<nums.length;i++){
            paths.add(nums[i]);
            backtracking(k,n,i+1,nums);
            paths.removeLast();
        }
    }
}

剪枝优化

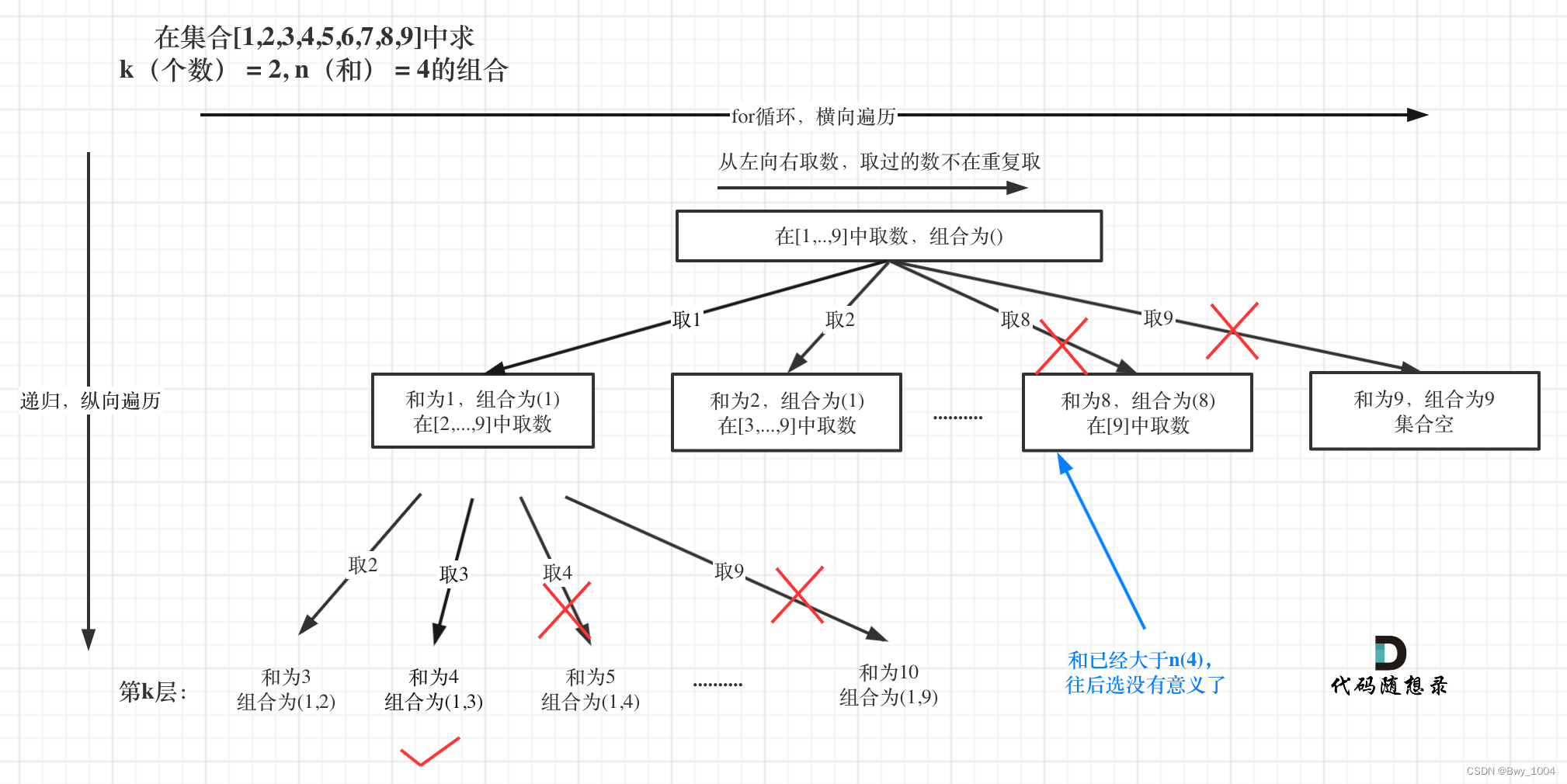
在这里插入图片描述
已选元素总和如果已经大于n（图中数值为4）了，那么往后遍历就没有意义了，直接剪掉。

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> paths = new LinkedList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
        backtracking(k,n,1,0);
        return res;
    }
    public void backtracking(int k,int n,int startIndex,int sum){
        if(sum>n){ //剪枝
            return ;
        }
        if(paths.size() == k){
            if(sum == n){
                //收集结果
                res.add(new ArrayList<>(paths));
                return ; 
            }
        }
        for(int i = startIndex;i<=9-(k-paths.size())+1;i++){
            paths.add(i);
            sum += i;
            backtracking(k,n,i+1,sum);
            paths.removeLast();
            sum -= i;
        }
    }
}

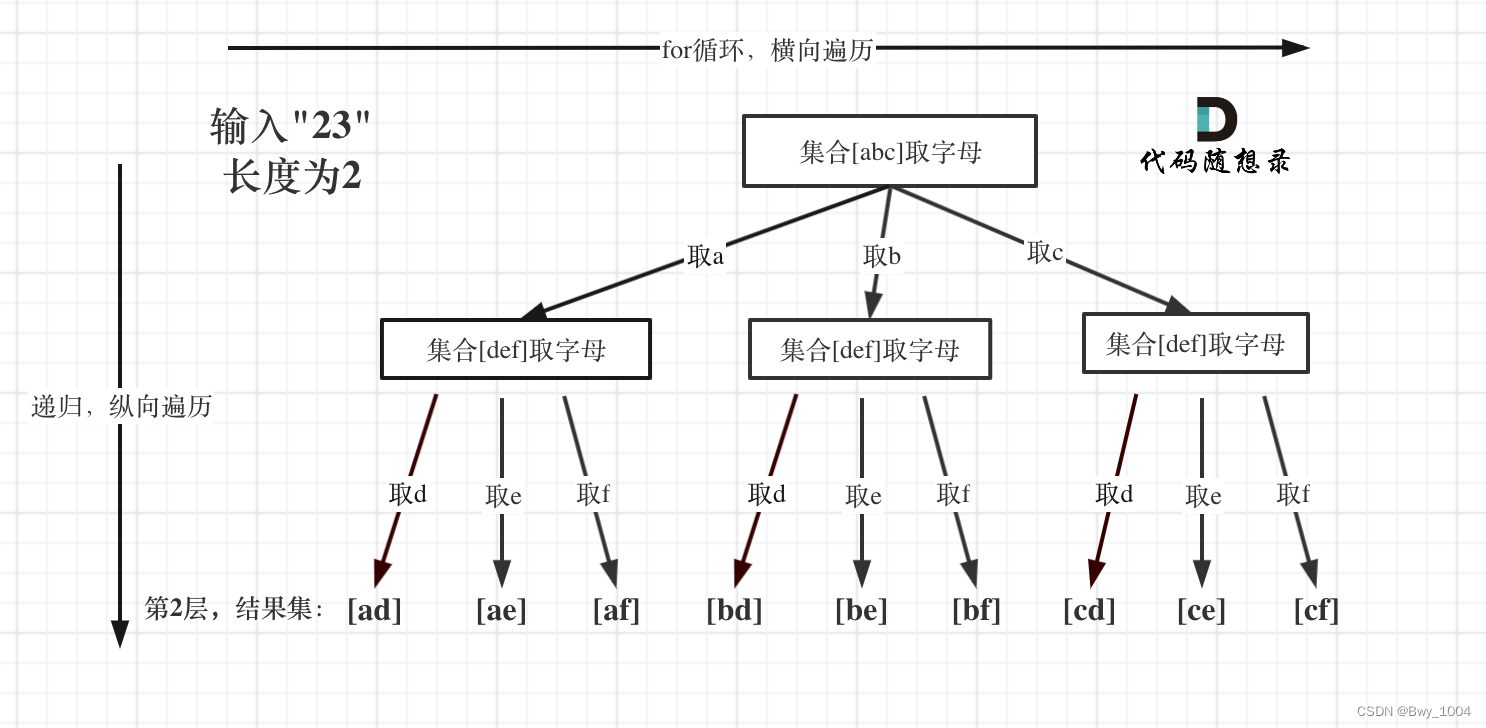
在这里插入图片描述

三、电话号码的字母组合（力扣17）

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按任意顺序返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。
在这里插入图片描述

class Solution {
    List<String> res = new ArrayList<>();
    public List<String> letterCombinations(String digits) {
        if(digits==null || digits.length()==0){
            return res;
        }
        //为了直接对应2-9，新增了两个无效的字符串“ ”
        String[] numString = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
        backtracking(digits,numString,0); 
        return res;
    }
    StringBuilder temp = new StringBuilder();
    public void backtracking(String digits,String[] numString,int num){
        if(num==digits.length()){
            res.add(temp.toString());
            return ;
        }

        String str = numString[digits.charAt(num)-'0'];
        for(int i=0;i<str.length();i++){
            temp.append(str.charAt(i));
            //递归
            backtracking(digits,numString,num+1);
            temp.deleteCharAt(temp.length()-1); //回溯，把最后一个加进去的元素进行删除

        }
    }
}

在这里插入图片描述

总结

回溯算法模板框架如下：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}