一提到 Redis，我们的脑子里马上就会出现一个词：“快。”但是你有没有想过，Redis 的快，到底是快在哪里呢？实际上，这里有一个重要的表现：它接收到一个键值对操作后，能以微秒级别的速度找到数据，并快速完成操作。

**数据库这么多，为啥 Redis 能有这么突出的表现呢？ **

• 一方面，这是因为它是内存数据库，所有的操作都在内存上完成，内存的访问速度本身就很快。
• 另一方面，这要归功于它的数据结构。这是因为，键值对是按一定的数据结构来组织的，操作键值对最终就是对数据结构进行增删改查操作，所以高效的数据结构是 Redis 快速处理数据的基础。

面试中经常会被问到：你说一下 Redis 中的数据结构

绝大多数的人都能回答上来这五个，String，List，Hash，Set，Zset这五个。

这么回答没有亮点，如果你能答上来每个数据结构的底层用了哪些数据类型就好了，其实上述五种每一个都都是由一个或者多个基本数据类型结合出来的，那接下来我们聊一下 Redis 的基本数据结构。

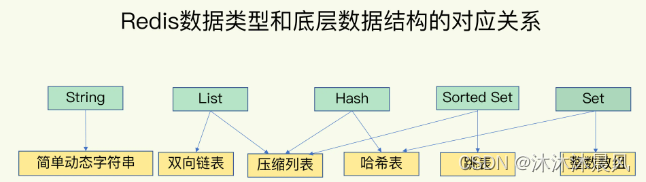
简单来说，底层数据结构一共有 6 种，分别是简单动态字符串、双向链表、压缩列表、哈希表、跳表和整数数组。 它们和数据类型的对应关系如下图所示：

Redis 使用了一个哈希表来存储所有键值对。

一个哈希表，其实就是一个数组，数组的每个元素称为一个哈希桶。所以，我们常说，一个哈希表是由多个哈希桶组成的，每个哈希桶中保存了键值对"数据"。

不管值是 String，还是集合类型，哈希桶中的元素都是指向它们的指针。

在下图中，可以看到，哈希桶中的 entry 元素中保存了key和value指针，分别指向了实际的键和值，这样一来，即使值是一个集合，也可以通过*value指针被查找到。

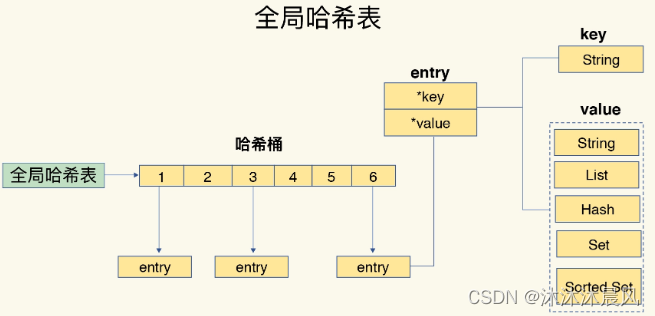
这个表叫做全局哈希表。

哈希表的最大好处很明显，就是让我们可以用 O(1) 的时间复杂度来快速查找到键值对——我们只需要计算键的哈希值，就可以知道它所对应的哈希桶位置，然后就可以访问相应的 entry 元素。

往 Redis 中插入数据突然变慢了，这是为什么呢？

可以考虑是不是哈希表的哈希冲突问题和 rehash 带来的操作阻塞。

为什么会产生哈希冲突呢？

这里的哈希冲突，比如说：两个 key 的哈希值通过哈希计算正好落在了一个哈希桶内。

Redis 解决哈希冲突的方式是用链式哈希法来解决。链式哈希也很容易理解，就是指同一个哈希桶中的多个元素用一个链表来保存，它们之间依次用指针连接。 如下图。

又来一个新的问题：如果冲突元素太多，有些哈希桶之下的拉链太长，这样寻找元素就不是哈希表的 O(1) 复杂度，而是 O(n) 了。

怎么解决拉链过长的问题呢？

Redis 会对哈希表做 rehash 操作。rehash 也就是增加现有的哈希桶数量，让逐渐增多的 entry 元素能在更多的桶之间分散保存，减少单个桶中的元素数量，从而减少单个桶中的冲突。那具体怎么做呢？

其实，为了使 rehash 操作更高效，Redis 默认使用了两个全局哈希表：哈希表 1 和哈希表 2。一开始，当你刚插入数据时，默认使用哈希表 1，此时的哈希表 2 并没有被分配空间。随着数据逐步增多，Redis 开始执行 rehash，这个过程分为三步：

1. 给哈希表 2 分配更大的空间，例如是当前哈希表 1 大小的两倍；
2. 把哈希表 1 中的数据重新映射并拷贝到哈希表 2 中；
3. 释放哈希表 1 的空间。

到此，我们就可以从哈希表 1 切换到哈希表 2，用增大的哈希表 2 保存更多数据，而原来的哈希表 1 留作下一次 rehash 扩容备用。

这个过程看似简单，但是第二步涉及大量的数据拷贝，如果一次性把哈希表 1 中的数据都迁移完，会造成 Redis 线程阻塞，无法服务其他请求。此时，Redis 就无法快速访问数据了。

怎么解决这个呢？

为了避免这个问题，Redis 采用了渐进式 rehash。

简单来说就是在第二步拷贝数据时，Redis 仍然正常处理客户端请求，每处理一个请求时，从哈希表 1 中的第一个索引位置开始，顺带着将这个索引位置上的所有 entries 拷贝到哈希表 2 中；等处理下一个请求时，再顺带拷贝哈希表 1 中的下一个索引位置的 entries。

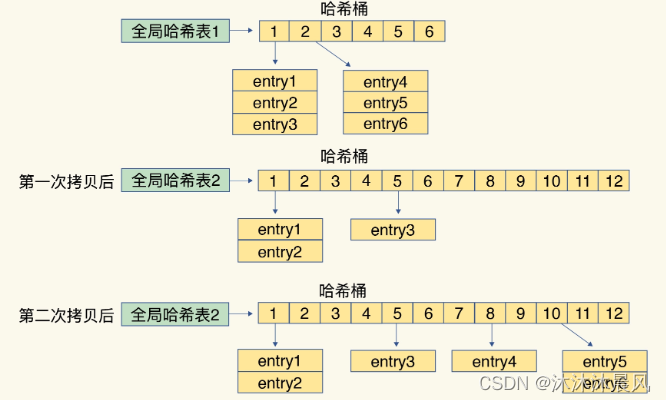
这样就巧妙地把一次性大量拷贝的开销，分摊到了多次处理请求的过程中，避免了耗时操作，保证了数据的快速访问。

有哪些底层数据结构？

集合类型的底层数据结构主要有 5 种：整数数组、双向链表、哈希表、压缩列表和跳表。

其中，哈希表的操作特点刚刚已经学过了；整数数组和双向链表也很常见，它们的操作特征都是顺序读写，也就是通过数组下标或者链表的指针逐个元素访问，操作复杂度基本是 O(N)，操作效率比较低；压缩列表和跳表我们平时接触得可能不多，但它们也是 Redis 重要的数据结构。

压缩列表是实际上是类似于一个数组。和数组不同的是，压缩列表在表头有三个字段 zlbytes、zltail 和 zllen，分别表示列表长度、列表尾的偏移量和列表中的 entry 个数；压缩列表在表尾还有一个 **zlend，**表示列表结束。

在压缩列表中，如果我们要查找定位第一个元素和最后一个元素，可以通过表头三个字段的长度直接定位，复杂度是 O(1)。而查找其他元素时，就没有这么高效了，只能逐个查找，此时的复杂度就是 O(N) 了。

跳表：

有序链表只能逐一查找元素，导致操作起来非常缓慢，于是就出现了跳表。具体来说，跳表在链表的基础上，增加了多级索引，通过索引位置的几个跳转，实现数据的快速定位，如下图所示：

如果我们要在链表中查找 33 这个元素，只能从头开始遍历链表，查找 6 次，直到找到 33 为止。此时，复杂度是 O(N)，查找效率很低。

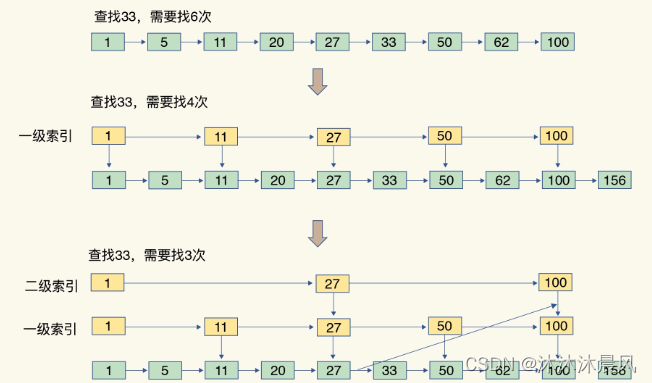
为了提高查找速度，我们来增加一级索引：从第一个元素开始，每两个元素选一个出来作为索引。这些索引再通过指针指向原始的链表。例如，从前两个元素中抽取元素 1 作为一级索引，从第三、四个元素中抽取元素 11 作为一级索引。此时，我们只需要 4 次查找就能定位到元素 33 了。

如果我们还想再快，可以再增加二级索引：从一级索引中，再抽取部分元素作为二级索引。例如，从一级索引中抽取 1、27、100 作为二级索引，二级索引指向一级索引。这样，我们只需要 3 次查找，就能定位到元素 33 了。

可以看到，这个查找过程就是在多级索引上跳来跳去，最后定位到元素。这也正好符合“跳”表的叫法。当数据量很大时，跳表的查找复杂度就是 O(logN)。

现在可以按照查找的时间复杂度给这些数据结构分下类了：

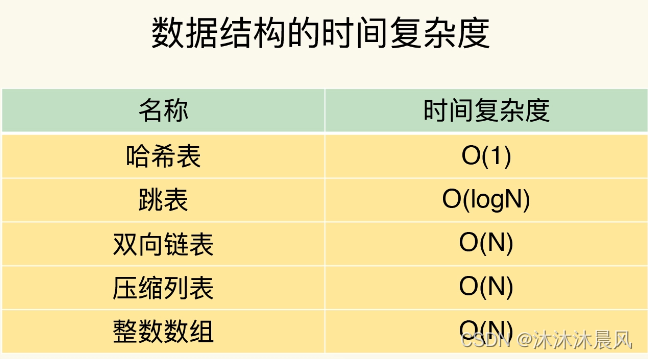
如何去选择合适的数据结构呢？

看你的具体场景

• 如果统计操作做的多，那就可以使用采用压缩列表的数据结构。

• 如果经常操作头尾元素数据的话，那就可以采用例如压缩列表和双向链表，它们都会记录表头和表尾的偏移量。