写在前面：NSGA III算法在数学上比NSGA II算法要复杂得多，尤其是在参考点那里，我也不是看得很明白，所以这篇文章只是尝试梳理下NSGA III的整体改进思路和优势，不对函数、公式、代码之类的细节做过多分析。如有错误，恳请指出！

算法简介

NSGA-III（Non-dominated Sorting Genetic Algorithm III）算法是NSGA-II的改进版，是多目标优化领域中的重要算法之一。该算法在选择机制上进行了创新，通过引入广泛分布的参考点来维持种群的多样性，其关键优势在于其能够有效地平衡多样性和收敛性，以找到Pareto前沿上的高质量解。

NSGA-III的主体框架与NSGA II基本一致，其主要步骤如下：

1. 初始化种群：

   • 随机生成一个初始种群，其中包含多个个体（解）。
   • 每个个体通常由一组决策变量表示。

2. 非支配排序：

   • 对初始种群中的个体进行非支配排序。
   • 将个体分为不同的等级，其中第一级包含Pareto前沿上的非支配解，第二级包含被第一级支配的解，以此类推。
   • 计算每个解的拥挤度，以度量其在前沿中的密度。

3. 选择操作：

   • 选择一部分解用于创建下一代种群。
   • 选择前几个非支配级别中的所有解，以确保高质量的解被保留。
   • 对于同一等级的解，根据它们的拥挤度选择一部分以维持多样性。
   • 选择的解将进入下一代种群。

4. 交叉和变异：

   • 使用交叉和变异操作生成下一代解。
   • 通过交叉操作，两个父代解可以产生一个或多个子代解。
   • 通过变异操作，对个体的决策变量进行微小的随机变化。

5. 更新种群：

   • 将新生成的解与上一代种群合并，形成新的2N种群。
   • 如果种群大小超过所需大小，可以使用选择策略来选择最适合的解。

6. 迭代：

   • 检查终止条件是否满足。通常，可以设置最大迭代次数或其他收敛标准作为终止条件。
   • 如果终止条件未满足，返回步骤2，继续进行下一代进化。
   • 如果满足终止条件，输出结果。返回找到的Pareto前沿上的高质量解集合作为算法的输出。

NSGA-III的关键特点是它的能力维护多样性和寻找Pareto前沿上的高质量解。它通过非支配排序、环境选择和多样性维护策略来实现这些目标，使其在多目标优化问题中非常有效。

多目标问题

为什么会有NSGA III算法？

NSGA III算法是从NSGA II算法改进改进过来的，其出现的原因自然是，NSGA II在求解一些问题的时候仍然存在局限性。两种算法各有其适应的问题特点，在原论文中，NSGA III算法的提出主要是期望求解Many-objective问题。

Multi-objective和Many-objective

原文：
Loosely,many-objective problems are defined as problems having four or more objectives.Two and three-objective prob lems fall into a different class as the resulting Pareto-optimal front,in most cases,in its totality can be comprehensively visualized using graphical means.Although a strict upper bound on the number of objectives for a many-objective optimization problem is not so clear,except a few occasions [15],most practitioners are interested in a maximum of 10 to 15 objectives.

简单来说，当一个多目标优化问题包含4个或更多的目标函数时，人们会倾向于将其视为 “Many-objective” 问题。这是因为在目标函数数量增加时，问题的复杂性显著增加，解决方案的多样性变得更加关键，同时性能评估也更加具有挑战性。

即：

• Multi-objective→2-3个目标函数；
• Many-objective→4个及以上（通常为10-15个）目标函数，

NSGA II→NSGA III

同上一篇NSGA II一样，这里直接梳理NSGA III相对于NSGA II的改进点。

由于NSGA III是在NSGA II的基础上，为求解Many-objective问题进行改进的，而Many-objective相对Multi-objective的一个显著特点就是，所谓量变引起质变，Many-objective的解空间相比Multi-objective要大得多，解的分布也显得比较稀疏，这就导致算法在对最优解进行搜索时，算法在某个解分布密度较大的地方，很容易陷入局部最优解。因此，NSGA III的改进主要针对于如何保留解的多样性，避免算法陷入局部最优，而保留解的多样性以及跳出局部最优的关键就在于一窜算法的选择操作。

为突出NSGA III的具体改进，根据原文献，可将其选择操作进一步细化成以下几个流程：

将种群划分为非支配性级别——确定超平面上的参考点——种群个体的自适应归一化——关联操作——小生境保留操作——生成子代种群的遗传操作

下面将根据这一流程介绍NSGA III在NSGA II的基础上进行的几点改进。

1. 多层级分层排序

NSGA-III引入了多层级分层排序，这是其最显著的改进。在NSGA-III中，种群被分为多个分层级别，每个级别包含不同密度的解决方案。这种分层排序使算法能够更好地维护Pareto前沿上的均匀分布解。

这个在上边的选择流程中没有明确的体现，但是我认为，NSGA III算法的精髓，就是解的层级分配和排序。

回想一下NSGA II算法的非支配排序，它是直接将父代和子代种群拼接成2N的心种群之后，再对这个2N种群进行排序。而NSGA III为了应对Many-objective问题的解在高维解空间上分布的稀疏性问题，不是直接对2N种群进行非支配排序，而是对种群中的个体（解）进行分层后，对每层进行非支配排序。实际上，NSGA III在解的搜索阶段，就已经通过类似统计学中分层采样的思想，对解进行了分层。

广为人知的参考点法，在我看来，是实现多层级分层排序的一个手段。

参考点具体是如何引入的呢？我看不懂公式，所以只能结合图和文字一点点来猜。

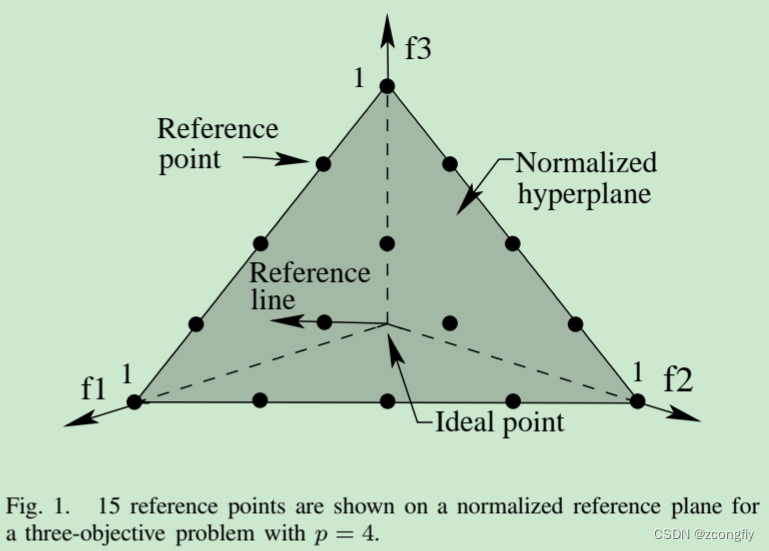
简单说就是，NSGA-III通过某种方法，从解空间中选择规定数量的、均匀分布的、能够覆盖整个目标空间的、自适应调整的参考点。这些参考点就相当于在解空间中打下的标记，告诉后续的解搜索算法，这里还有一块被标记的区域需要搜索，不要漏掉了。

一个个参考点以及参考点周围聚拢过来的候选解，慢慢地形成了解的不同层级（当然，可以将具有相似特征的参考点附近的解视为同一层级）。

多层级分层排序流程：

1. 选择参考点：NSGA-III选择一组参考点（reference points），这些点位于目标空间中，用于衡量解在目标空间中的优越性。通常，参考点是均匀分布的，以覆盖整个目标空间。
2. 分层级别的分配：接下来，将解分配到不同的层级级别。解的分配基于它们与参考点的比较，具体来说，是解与最接近的参考点之间的距离。每个解被分配到最接近的参考点所对应的层级级别。
3. 级级别的排序：在每个层级级别内，使用非支配排序（non-dominated sorting）将解排序。这是为了确定解的非支配性，即解是否在该层级内不被其他解所支配。
4. 选择解：从每个层级级别中选择一定数量的解，以形成新一代的种群。通常，选择的策略可能包括非支配排序和拥挤度（crowding distance）的考虑，以确保选择均匀分布在每个层级内。

通过这种方式，NSGA-III能够确保解在Pareto前沿上的分布均匀，并且可以更好地逼近Pareto前沿。参考点的选择和解的分配是多层级分层排序的核心概念，使算法能够有效地处理多目标优化问题，维护均匀分布的解，提高性能。

2. 种群个体的自适应归一化

NSGA-III算法中的自适应归一化是对每个个体的目标函数值进行的归一化。这是为了将不同目标之间的值进行比较，并确定个体在多目标优化中的相对优越性。自适应归一化通常通过与参考点之间的距离来实现，这些参考点通常均匀分布在目标空间中。

具体来说，对于每个个体，NSGA-III计算它与每个参考点之间的距离。然后，通过将个体到最近参考点的距离作为归一化值，确定个体在目标空间中的优越性。这有助于选择具有不同优越性的个体，并维持解在Pareto前沿上的均匀分布。

自适应归一化是NSGA-III算法的一个关键概念，它有助于确定解的相对优越性，以支持多目标优化的解选择过程。这种归一化考虑了不同目标之间的权重和距离，以便更好地维持解的多样性和均匀分布。

3. 关联操作

在NSGA-III中，关联操作是用于将种群中的每个个体与参考点相关联的过程，以确定每个个体在多目标优化中的相对优越性。

关联操作流程如下：

1. 种群个体归一化：对于每个目标函数值，将其进行归一化，以将所有目标值映射到[0, 1]的范围内。这是为了确保不同目标之间的值具有可比性。
2. 计算与参考点的距离：对于每个个体，计算其与每个参考点之间的距离。通常使用欧氏距离或其他距离度量来计算。
3. 确定关联：将每个个体与最近的参考点关联。即，每个个体被认为与最近的参考点相关联，这将决定其在多目标空间中的位置。
4. 确定层级级别：基于关联的结果，将解分配到不同的层级级别。这有助于确保解的分布在多目标空间中均匀，以支持多样性和均匀性。

可以将NSGA-III中的关联操作视为一种类似于聚类的过程，将种群中的个体分组成多个类别，其中每个类别由最接近的参考点来定义。每个参考点代表不同的类别或群集，而个体与最接近的参考点相关联，意味着它们被归入相应的类别。

通过这个关联操作，NSGA-III能够确定每个个体在多目标空间中的相对位置，这将在后续的选择过程中用于选择解以构建下一代的种群。这个过程有助于维护多样性并更好地逼近Pareto前沿。

4. 小生境保留操作

在NSGA-III中，关联操作将每个个体与最近的参考点相关联。每个参考点及其周围关联的个体构成了一个聚类类别，这个聚类类别可以被视为一个小生境。每个小生境中的个体与同一个参考点具有相似的目标函数值，因此它们在目标空间中相对接近。在选择操作中，通常会从不同的小生境中选择个体，以确保选择的解具有广泛的多样性，从而更好地逼近Pareto前沿。小生境保留操作是NSGA-III算法维持多样性的关键机制之一。

小生境操作是在已经划分好各种小生境的基础上实现的，其目的是根据每个小生境的大小来选择个体以填充各自的小生境，从而维持多样性。在NSGA-III中，每个小生境（聚类类别，包括与参考点相关联的个体）都有一个预定的大小或容量，小生境的大小是由与参考点相关联的个体数量来决定的。在小生境操作中，目标是确保每个小生境内有足够的个体，以维持多样性和均匀分布。

因此，操作的目标是填充每个小生境，使其包含所需数量的个体。这些个体可以是从其他小生境中选择的，以确保每个小生境内的个体数量达到所需的大小。在填充小生境时，通常会选择与参考点关联度最高的个体，以确保它们在多目标空间中相对接近。

这个过程将重复进行，直到每个小生境都包含所需数量的个体。通过这种方式，NSGA-III确保了不同小生境内的个体数量均衡，并维持了多样性，以支持更好的多目标优化搜索。

小生境操作流程：

1. 计算小生境的大小：首先，确定每个小生境（关联的参考点和相关个体组成的聚类类别）的大小。小生境大小通常由与参考点相关联的个体数量（p_j）来决定。
2. 选择小生境：从已经划分好的小生境中，确定具有最小小生境计数的小生境集合 J。这些小生境将用于进行小生境操作。
3. 小生境操作：

• 对于每个选定的小生境 j，执行以下操作：
• 如果小生境 j 为空（p_j = 0），则需要从其他小生境（F_j）中选择一个与参考点 j 相关联的个体，通常是选择与参考线垂直距离最短的个体，并将其添加到小生境中（P+ 集合）。然后，增加小生境 j 的计数 p_j。
• 如果小生境 j 不为空（p_j > 0），则需要从小生境 j 中随机选择一个与参考点 j 相关联的个体，并将其添加到小生境中（P+1 集合）。然后，增加小生境 j 的计数 p_j。

4. 重复操作：上述小生境操作将在每个选定的小生境上重复，以确保小生境的填充。这个过程通常会重复 K 次，以确保 P+ 集合中的所有空位置都被填充。

5. 无参数特性

与NSGA-Ⅱ一样，NSGA-Ⅲ算法除了通常的遗传参数如种群规模、终止参数、交叉和变异概率及其相关参数外，不需要设置任何新的参数。参考点的数量H 不是一个算法参数，因为这完全由用户来决定。种群规模N 取决于H ，因为N≈H。参考点的位置同样取决于用户对所获得的解中的偏好信息。

代码

参考：https://github.com/Xavier-MaYiMing/NSGA-III

import numpy as np
import matplotlib.pyplot as plt
from collections import Counter
from itertools import combinations  # 创建和操作迭代器的工具
from scipy.linalg import LinAlgError    # 用于处理线性代数相关的错误
from scipy.spatial.distance import cdist    # 用于计算距离或相似性


def cal_obj(pop, nobj):
    '''
    :param pop: ndarray，决策变量的取值，形状为(N, D)，N为种群中个体的数量，D为决策变量的数量
    :param nobj: int，目标函数的数量
    :return: ndarray，计算得到的目标函数值，形状为(N, nobj)，N是种群中个体的数量，nobj是目标函数的数量。
    '''
    # 这里的函数是 DTLZ1 函数，用于多目标优化问题。g 是一个中间变量。
    g = 100 * (pop.shape[1] - nobj + 1 + np.sum(
        (pop[:, nobj - 1:] - 0.5) ** 2 - np.cos(20 * np.pi * (pop[:, nobj - 1:] - 0.5)), axis=1))

    objs = np.zeros((pop.shape[0], nobj))   # 创建一个大小为 (pop.shape[0], nobj) 的零矩阵，用于存储目标函数值。

    temp_pop = pop[:, : nobj - 1]   # 从输入的 pop 矩阵中取出前 nobj-1 列，存储在 temp_pop 中。

    for i in range(nobj):   # 遍历目标函数的数量（nobj）
        f = 0.5 * (1 + g)   # 计算 f，其中 g 是前面计算的中间变量。

        f *= np.prod(temp_pop[:, : temp_pop.shape[1] - i], axis=1)  # 使用累积乘法计算 f 的一部分，这部分与 temp_pop 相关。

        if i > 0:
            f *= 1 - temp_pop[:, temp_pop.shape[1] - i]     # 如果 i 大于 0，再乘以 1 减去 temp_pop 的一部分。

        objs[:, i] = f  # 将计算得到的 f 存储在目标函数矩阵的第 i 列。

    return objs


def factorial(n):
    # calculate n!
    if n == 0 or n == 1:
        return 1
    else:
        return n * factorial(n - 1)


def combination(n, m):
    # choose m elements from an n-length set
    # 计算排列组合数C(n,m)
    if m == 0 or m == n:
        return 1
    elif m > n:
        return 0
    else:
        return factorial(n) // (factorial(m) * factorial(n - m))


def reference_points(npop, nvar):
    '''
    calculate approximately npop uniformly distributed reference points on nvar dimensions
    :param npop: int，要生成的均匀分布的参考点的数量
    :param nvar: int，参考点的维度
    :return: ndarray，所生成的均匀分布的参考点的坐标，形状为(npop, nvar)
    '''
    h1 = 0  # 用于控制循环的计数器
    while combination(h1 + nvar, nvar - 1) <= npop: # 目的是确定一个足够大的h1，以便在nvar-1维度上有足够的均匀分布的参考点。
        h1 += 1
    # 使用组合数的计算结果，构建一个 points 数组，这个数组包含了 h1 维度中的参考点坐标
    points = np.array(list(combinations(np.arange(1, h1 + nvar), nvar - 1))) - np.arange(nvar - 1) - 1
    # 对 points 数组中的坐标进行变换，以确保它们在 [0, 1] 范围内均匀分布
    points = (np.concatenate((points, np.zeros((points.shape[0], 1)) + h1), axis=1) - np.concatenate((np.zeros((points.shape[0], 1)), points), axis=1)) / h1
    if h1 < nvar:   # 如果h1不足以在nvar-1维度上生成足够多的参考点
        h2 = 0
        # h2 的值，以便在nvar-1维度上有足够多的均匀分布的参考点。这些参考点将与之前的points组合在一起。
        while combination(h1 + nvar - 1, nvar - 1) + combination(h2 + nvar, nvar - 1) <= npop:
            h2 += 1
        if h2 > 0:
            # 使用上边类似的方式，构建temp_points数组，然后进行坐标变换
            temp_points = np.array(list(combinations(np.arange(1, h2 + nvar), nvar - 1))) - np.arange(nvar - 1) - 1
            temp_points = (np.concatenate((temp_points, np.zeros((temp_points.shape[0], 1)) + h2), axis=1) - np.concatenate((np.zeros((temp_points.shape[0], 1)), temp_points), axis=1)) / h2
            temp_points = temp_points / 2 + 1 / (2 * nvar)
            # 将temp_points添加到points中，以得到最终的参考点数组，并将其返回
            points = np.concatenate((points, temp_points), axis=0)
    return points


def nd_sort(objs):
    """
    fast non-domination sort
    :param objs: ndarray，种群中每个个体的目标函数值，形状为(npop, nobj)，其中npop是种群中个体的数量，nobj是目标函数的数量。
    :return pfs: dict，键表示非支配级别，对应的值是一个包含相应级别的Pareto前沿中的个体索引的列表。
    :return rank: ndarray，每个个体的非支配级别，形状为 (npop,)，其中npop是种群中个体的数量。rank数组指示了每个个体所属的非支配级别
    """
    (npop, nobj) = objs.shape
    n = np.zeros(npop, dtype=int)  # the number of individuals that dominate this individual
    s = []  # the index of individuals that dominated by this individual
    rank = np.zeros(npop, dtype=int)
    ind = 0
    pfs = {ind: []}  # Pareto fronts
    for i in range(npop):
        s.append([])
        for j in range(npop):
            if i != j:
                less = equal = more = 0
                for k in range(nobj):
                    if objs[i, k] < objs[j, k]:
                        less += 1
                    elif objs[i, k] == objs[j, k]:
                        equal += 1
                    else:
                        more += 1
                if less == 0 and equal != nobj:
                    n[i] += 1
                elif more == 0 and equal != nobj:
                    s[i].append(j)
        if n[i] == 0:
            pfs[ind].append(i)
            rank[i] = ind
    while pfs[ind]:
        pfs[ind + 1] = []
        for i in pfs[ind]:
            for j in s[i]:
                n[j] -= 1
                if n[j] == 0:
                    pfs[ind + 1].append(j)
                    rank[j] = ind + 1
        ind += 1
    pfs.pop(ind)
    return pfs, rank


def selection(pop, pc, rank, k=2):
    """
    binary tournament selection
    :param pop: ndarray，种群中每个个体的决策变量值，形状为(npop,nvar)，即（种群中个体数量，决策变量数量）
    :param pc: float，选择概率
    :param rank: ndarray，每个个体的非支配级别，形状为(npop,)，即（种群中个体数，）
    :param k: 锦标赛选择中参与竞争的个体数量
    :return: ndarray，选择后得到的用于繁殖的个体的决策变量值，形状为(nm,nvar)，nm为选择个体数量，通常等于npop*pc，确保为偶数
    """
    (npop, nvar) = pop.shape
    nm = int(npop * pc)
    nm = nm if nm % 2 == 0 else nm + 1
    mating_pool = np.zeros((nm, nvar))
    for i in range(nm):
        [ind1, ind2] = np.random.choice(npop, k, replace=False)
        if rank[ind1] <= rank[ind2]:
            mating_pool[i] = pop[ind1]
        else:
            mating_pool[i] = pop[ind2]
    return mating_pool


def crossover(mating_pool, lb, ub, pc, eta_c):
    """
    simulated binary crossover (SBX) 模拟二进制交叉
    :param mating_pool: ndarray用于繁殖的个体的决策变量值，形状(noff,nvar)，即（要繁殖的个体数，决策变量数）
    :param lb: ndarray，决策变量下界(lower bound)，形状(nvar,)
    :param ub: ndarray，决策变量上界(upper bound)，形状(nvar,)
    :param pc: float，交叉概率
    :param eta_c: int，扩散因子分布指数，用于控制模拟二进制交叉的分布情况，值越大（>10），分布越均匀
    :return: ndarray，交叉结果，形状为(noff, nvar)
    """
    (noff, nvar) = mating_pool.shape
    nm = int(noff / 2)
    parent1 = mating_pool[:nm]  #拆分
    parent2 = mating_pool[nm:]
    beta = np.zeros((nm, nvar))
    mu = np.random.random((nm, nvar))
    flag1 = mu <= 0.5
    flag2 = ~flag1
    beta[flag1] = (2 * mu[flag1]) ** (1 / (eta_c + 1))
    beta[flag2] = (2 - 2 * mu[flag2]) ** (-1 / (eta_c + 1))
    beta = beta * (-1) ** np.random.randint(0, 2, (nm, nvar))
    beta[np.random.random((nm, nvar)) < 0.5] = 1
    beta[np.tile(np.random.random((nm, 1)) > pc, (1, nvar))] = 1
    offspring1 = (parent1 + parent2) / 2 + beta * (parent1 - parent2) / 2   # 交叉
    offspring2 = (parent1 + parent2) / 2 - beta * (parent1 - parent2) / 2
    offspring = np.concatenate((offspring1, offspring2), axis=0)    # 重新拼接
    offspring = np.min((offspring, np.tile(ub, (noff, 1))), axis=0)
    offspring = np.max((offspring, np.tile(lb, (noff, 1))), axis=0)
    return offspring


def mutation(pop, lb, ub, pm, eta_m):
    """
    polynomial mutation 多项式变异
    :param pop: ndarray用于繁殖的个体的决策变量值，形状(noff,nvar)，即（要繁殖的个体数，决策变量数）
    :param lb: ndarray，决策变量下界(lower bound)，形状(nvar,)
    :param ub: ndarray，决策变量上界(upper bound)，形状(nvar,)
    :param pm: float，变异概率
    :param eta_m: 扰动因子分布指数，用于控制多项式变异的分布形状，值很大时，变异幅度较小，变异的形状更趋于均匀分布
    :return: ndarray，交叉结果，形状为(noff, nvar)
    """
    (npop, nvar) = pop.shape
    lb = np.tile(lb, (npop, 1))
    ub = np.tile(ub, (npop, 1))
    site = np.random.random((npop, nvar)) < pm / nvar
    mu = np.random.random((npop, nvar))
    delta1 = (pop - lb) / (ub - lb)
    delta2 = (ub - pop) / (ub - lb)
    temp = np.logical_and(site, mu <= 0.5)
    pop[temp] += (ub[temp] - lb[temp]) * ((2 * mu[temp] + (1 - 2 * mu[temp]) * (1 - delta1[temp]) ** (eta_m + 1)) ** (1 / (eta_m + 1)) - 1)
    temp = np.logical_and(site, mu > 0.5)
    pop[temp] += (ub[temp] - lb[temp]) * (1 - (2 * (1 - mu[temp]) + 2 * (mu[temp] - 0.5) * (1 - delta2[temp]) ** (eta_m + 1)) ** (1 / (eta_m + 1)))
    pop = np.min((pop, ub), axis=0)
    pop = np.max((pop, lb), axis=0)
    return pop


def environmental_selection(pop, objs, zmin, npop, V):
    """
    NSGA-III environmental selection
    :param pop: ndarray，用于繁殖的个体的决策变量值，形状(noff,nvar)，即（要繁殖的个体数，决策变量数）
    :param objs: ndarray，种群中每个个体的目标函数值，形状为 (npop, nobj)，nobj 是目标函数的数量。
    :param zmin: ndarray，每个目标函数的最小值。它的形状为 (nobj,)
    :param npop: int，环境选择后要保留的个体数量
    :param V: 权向量，用于计算多目标优化中的 Pareto 前沿，形状通常是 (nv, nobj)，即（权向量的数量，目标函数的数量）每个权向量代表一种目标函数权重的组合
    :return:
    """
    pfs, rank = nd_sort(objs)
    nobj = objs.shape[1]
    selected = np.full(pop.shape[0], False)
    ind = 0
    while np.sum(selected) + len(pfs[ind]) <= npop:
        selected[pfs[ind]] = True
        ind += 1
    K = npop - np.sum(selected)

    # select the remaining K solutions
    objs1 = objs[selected]
    objs2 = objs[pfs[ind]]
    npop1 = objs1.shape[0]
    npop2 = objs2.shape[0]
    nv = V.shape[0]
    temp_objs = np.concatenate((objs1, objs2), axis=0)
    t_objs = temp_objs - zmin

    # extreme points
    extreme = np.zeros(nobj)
    w = 1e-6 + np.eye(nobj)
    for i in range(nobj):
        extreme[i] = np.argmin(np.max(t_objs / w[i], axis=1))

    # intercepts
    try:
        hyperplane = np.matmul(np.linalg.inv(t_objs[extreme.astype(int)]), np.ones((nobj, 1)))
        if np.any(hyperplane == 0):
            a = np.max(t_objs, axis=0)
        else:
            a = 1 / hyperplane
    except LinAlgError:
        a = np.max(t_objs, axis=0)
    t_objs /= a.reshape(1, nobj)

    # association
    cosine = 1 - cdist(t_objs, V, 'cosine')
    distance = np.sqrt(np.sum(t_objs ** 2, axis=1).reshape(npop1 + npop2, 1)) * np.sqrt(1 - cosine ** 2)
    dis = np.min(distance, axis=1)
    association = np.argmin(distance, axis=1)
    temp_rho = dict(Counter(association[: npop1]))
    rho = np.zeros(nv)
    for key in temp_rho.keys():
        rho[key] = temp_rho[key]

    # selection
    choose = np.full(npop2, False)
    v_choose = np.full(nv, True)
    while np.sum(choose) < K:
        temp = np.where(v_choose)[0]
        jmin = np.where(rho[temp] == np.min(rho[temp]))[0]
        j = temp[np.random.choice(jmin)]
        I = np.where(np.bitwise_and(~choose, association[npop1:] == j))[0]
        if I.size > 0:
            if rho[j] == 0:
                s = np.argmin(dis[npop1 + I])
            else:
                s = np.random.randint(I.size)
            choose[I[s]] = True
            rho[j] += 1
        else:
            v_choose[j] = False
    selected[np.array(pfs[ind])[choose]] = True
    return pop[selected], objs[selected], rank[selected]


def main(npop, iter, lb, ub, nobj=3, pc=1, pm=1, eta_c=30, eta_m=20):
    """
    The main function
    :param npop: population size
    :param iter: iteration number
    :param lb: lower bound
    :param ub: upper bound
    :param nobj: the dimension of objective space
    :param pc: crossover probability (default = 1)
    :param pm: mutation probability (default = 1)
    :param eta_c: spread factor distribution index (default = 30) 扩散因子分布指数
    :param eta_m: perturbance factor distribution index (default = 20) 扰动因子分布指数
    :return:
    """
    # Step 1. Initialization
    nvar = len(lb)  # the dimension of decision space
    pop = np.random.uniform(lb, ub, (npop, nvar))  # population
    objs = cal_obj(pop, nobj)  # objectives
    V = reference_points(npop, nobj)  # reference vectors
    zmin = np.min(objs, axis=0)  # ideal points
    [pfs, rank] = nd_sort(objs)  # Pareto rank

    # Step 2. The main loop
    for t in range(iter):

        if (t + 1) % 50 == 0:
            print('Iteration: ' + str(t + 1) + ' completed.')

        # Step 2.1. Mating selection + crossover + mutation
        mating_pool = selection(pop, pc, rank)
        off = crossover(mating_pool, lb, ub, pc, eta_c)
        off = mutation(off, lb, ub, pm, eta_m)
        off_objs = cal_obj(off, nobj)

        # Step 2.2. Environmental selection
        zmin = np.min((zmin, np.min(off_objs, axis=0)), axis=0)
        pop, objs, rank = environmental_selection(np.concatenate((pop, off), axis=0), np.concatenate((objs, off_objs), axis=0), zmin, npop, V)

    # Step 3. Sort the results
    pf = objs[rank == 0]
    ax = plt.figure().add_subplot(111, projection='3d')
    ax.view_init(45, 45)
    x = [o[0] for o in pf]
    y = [o[1] for o in pf]
    z = [o[2] for o in pf]
    ax.scatter(x, y, z, color='red')
    ax.set_xlabel('objective 1')
    ax.set_ylabel('objective 2')
    ax.set_zlabel('objective 3')
    plt.title('The Pareto front of DTLZ1')
    plt.savefig('Pareto front')
    plt.show()


if __name__ == '__main__':
    main(91, 400, np.array([0] * 7), np.array([1] * 7))