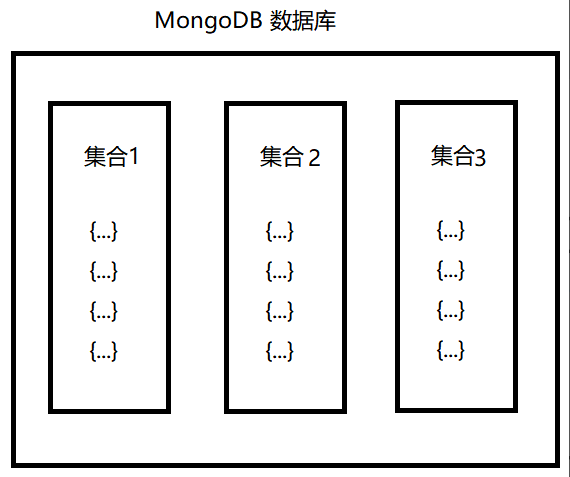
目录
- 概述
- 细节
- anchor-base vs anchor free
- 网络结构
- 标注
- 损失函数
- 学习资料
概述
本文是一个anchor-free的目标检测算法。
【2019】【CenterNet】
研究的问题:
- 如何更好地将目标检测问题建模为关键点检测问题
提出的方法:
- 一个简单高效的目标检测方法CenterNet。简单:彻底的端到端(不需要NMS后处理),整体流程就是关键点预测+相关参数回归,高效:不需要预先设置anchor,速度精度都超过了基于anchor的方法。
细节
anchor-base vs anchor free
anchor-base的流程:一阶段:预设大量的anchor,然后直接回归位置、尺寸和类别信息,选出其中达到要求的边界框作为预测框,然后使用NMS剔除重复的预测框。两阶段:预设大量的anchor,然后通过一个网络回归位置、尺寸和类别信息(包含物体的正例/不包含物体的负例),选出其中的正例作为候选框,然后再使用一个网络提取候选框特征,对候选框进行微调,得到检测框。总结:就是一个滑动窗口的思路,在图像中设计大量的anchor,然后在anchor中找到满足要求的检测框。而我们都知道一般一张图像中的目标是很有限的,所以基于anchor的方法会存在严重的正负样本不均衡问题,所以一阶段方法最开始预测框的数量不多,精度不够,直到后面出现了focal loss,而两阶段方法通过RPN网络大大减少负样本的数量。
anchor free的流程:类似于一阶段方法,结构都是特征提取网络+检测头。
anchor free和one-stage的区别:
- 仅仅使用位置区别正负样本,而非IOU
- 每个物体对应一个正样本,所以不需要NMS去重了
- 特征图的尺寸特别大(输出分辨率的下采样因子比较小),所以不需要多种不同的anchor了(每个像素只对应一个点的类别以及相关参数,一阶段方法中每个像素会对应多个anchor的类别以及相关参数)
网络结构
流程比较简单,就是特征提取网络+3个检测头
- 输入图像尺寸为 W ∗ H ∗ 3 W*H*3 W∗H∗3
- 经过特征提取网络得到特征图
- 第一个检测头的输出是关键点热力图,尺寸为 W R ∗ H R ∗ C \frac{W}{R}*\frac{H}{R}*C RW∗RH∗C,其中R是下采样因子这里会比一般检测器的因子小(论文中是4),C是类别数,如coco数据集的80。表示当前点作为中心的边界框的类别概率分布。
- 第二个检测头的输出是尺寸的预测结果,尺寸为 W R ∗ H R ∗ 2 \frac{W}{R}*\frac{H}{R}*2 RW∗RH∗2,表示当前点作为中心的边界框的尺寸( w , h w,h w,h)。
- 第三个检测头的输出是位置偏移量的预测结果,尺寸为 W R ∗ H R ∗ 2 \frac{W}{R}*\frac{H}{R}*2 RW∗RH∗2,表示当前点作为中心的边界框的中心偏移量( Δ x , Δ y \Delta x,\Delta y Δx,Δy)。

注:
第三个检测头输出的是位置的偏移量,那基本的位置信息是?为什么需要预测偏移量?
特征图的当前位置映射回原图中的位置就是 ( x , y ) (x,y) (x,y)。之前因为下采样的过程中是取整的,所以位置难免会有偏差,这个偏差就是由第三个检测头学习的,所以给第三个检测头的标签就是 ( x R − ⌊ x R ⌋ , y R − ⌊ y R ⌋ ) (\frac{x}{R}-\lfloor \frac{x}{R} \rfloor,\frac{y}{R}-\lfloor \frac{y}{R} \rfloor) (Rx−⌊Rx⌋,Ry−⌊Ry⌋)
为什么后面两个检测头输出通道数是2,而不是2C?
假设特征图中每个点最多对应一个目标,也就是原图像中目标的中心点不重合,且下采样之后依旧不重合,那么每个点就只需要对应一个尺寸、一个位置偏移就好了。
而不满足这个假设的数据在数据集中占据的比例非常的小,所以方案是合理的
标注
其实就是由边界框的坐标得到中心点的坐标以及宽高,然后下采样得到特征图上的坐标,对应位置的类别就是1,其余位置的类别就是0,然后把对应的尺寸以及偏移也填上去就好了。
这样做的话后面两个检测头是没有问题的,但是第一个检测头会有问题,就是对模型的要求太高了,作者用了一个高斯核将关键点分布到特征图上,其实也就是从关键点位置是1其余全部是0,变为了关键点位置是1点周围位置稍微小一点其余位置全是0,也就是在这个范围内的预测都能接受。
损失函数
损失主要是三部分,分别就是三个检测头的损失

其中第一个关键点热力图损失,采用的是修改了的focal loss
原来的focal loss是处理正负样本不均衡的交叉熵损失,因此类别只有0和1。原本关键点热力图的标签确实是0和1,但在引入了高斯核之后,就有中间的值了,作者在otherwise中添加了一项
(
1
−
Y
)
β
(1-Y)^\beta
(1−Y)β,如果原本的标签是0,这一项就没有用,而若是原本标签很大,就代表已经很接近关键点了,从而损失就比较小。

学习资料
吹爆!清华大佬硬核解读CenterNet目标检测算法!