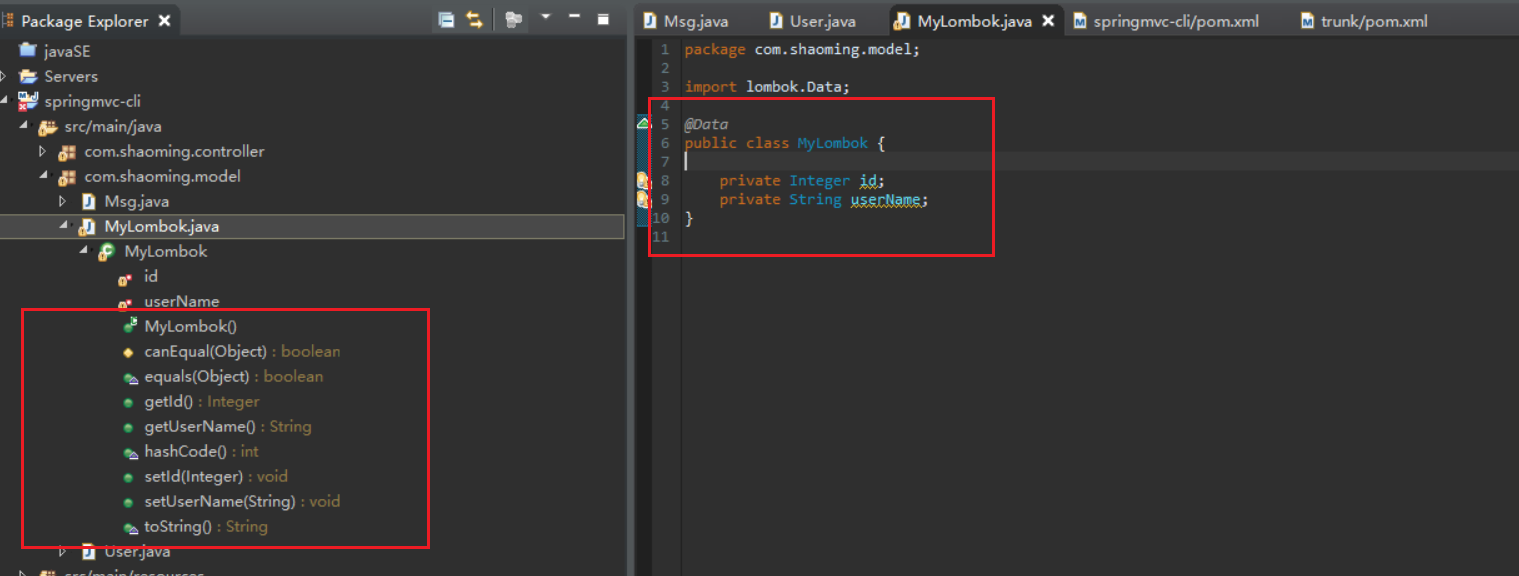
基于最长上升子序列 LIS

---

$求最长上升子序列有两种做法$
$一种是n^2复杂度的线性dp$
$另一种是O(nlogn)复杂度的贪心+二分$

贪心+二分做法

$整体思路就是维护一个low[]数组，让数组长度等于当前最长子序列长度$
$用ans表示当前low数组长度$
$当当前值大于low[ans]时low[++ans]=当前值$
$当当前值小于low[ans]时利用二分找到在low数组中当前值所在的位置然后替换为当前值$
$low[find(当前值)]=当前值$
$目的就是保证low数组是当前最长的上升子序列$

代码

---

#include<bits/stdc++.h>

using namespace std;

const int N = 1e3 + 10;

typedef long long ll;

ll low[N], arr[N];

int n;

int find(ll x, int len)
{
    int l = 1;
    int r = len;
    while(l < r)
    {
        int mid = l + r >> 1;
        
        if(low[mid] >= x)
        {
            r = mid;
        }
        else l = mid + 1;
    }
    
    return l;
}

int main()
{
    cin >> n;
    
    for(int i = 1; i <= n; i ++)
    {
        scanf("%lld", &arr[i]);
    }
    
    int ans = 1;
    
    low[ans] = arr[1]; //一开始第一个数就是最长上升子序列
    
    for(int i = 2; i <= n; i ++)
    {
        if(arr[i] > low[ans])
        {
            low[++ans] = arr[i];
        }
        else
        {
            low[find(arr[i],ans)] = arr[i];
        }
    }
    
    cout << ans << endl;
    
    return 0;
}

---

线性dp做法

---

#include<bits/stdc++.h>

using namespace std;

const int N = 1e4 + 10;

typedef long long ll;

ll arr[N];

int f[N];

int n;

int main()
{
    cin >> n;
    
    for(int i = 1; i <= n; i ++)
    {
        scanf("%lld", &arr[i]);
    }
    
    int res = 0;
    
    for(int i = 1; i <= n; i ++)
    {
        f[i] = 1; //初始化 每个数结尾最开始都是长度为1的LIS
        
        for(int j = 1; j < i; j ++)
        {
            if(arr[i] > arr[j])
            f[i] = max(f[i], f[j] +1);
        }
    }
    
    for(int i = 1; i <= n; i ++)
    {
        res = max(res, f[i]);
    }
    
    cout << res << endl;
    
    return 0;
}

---