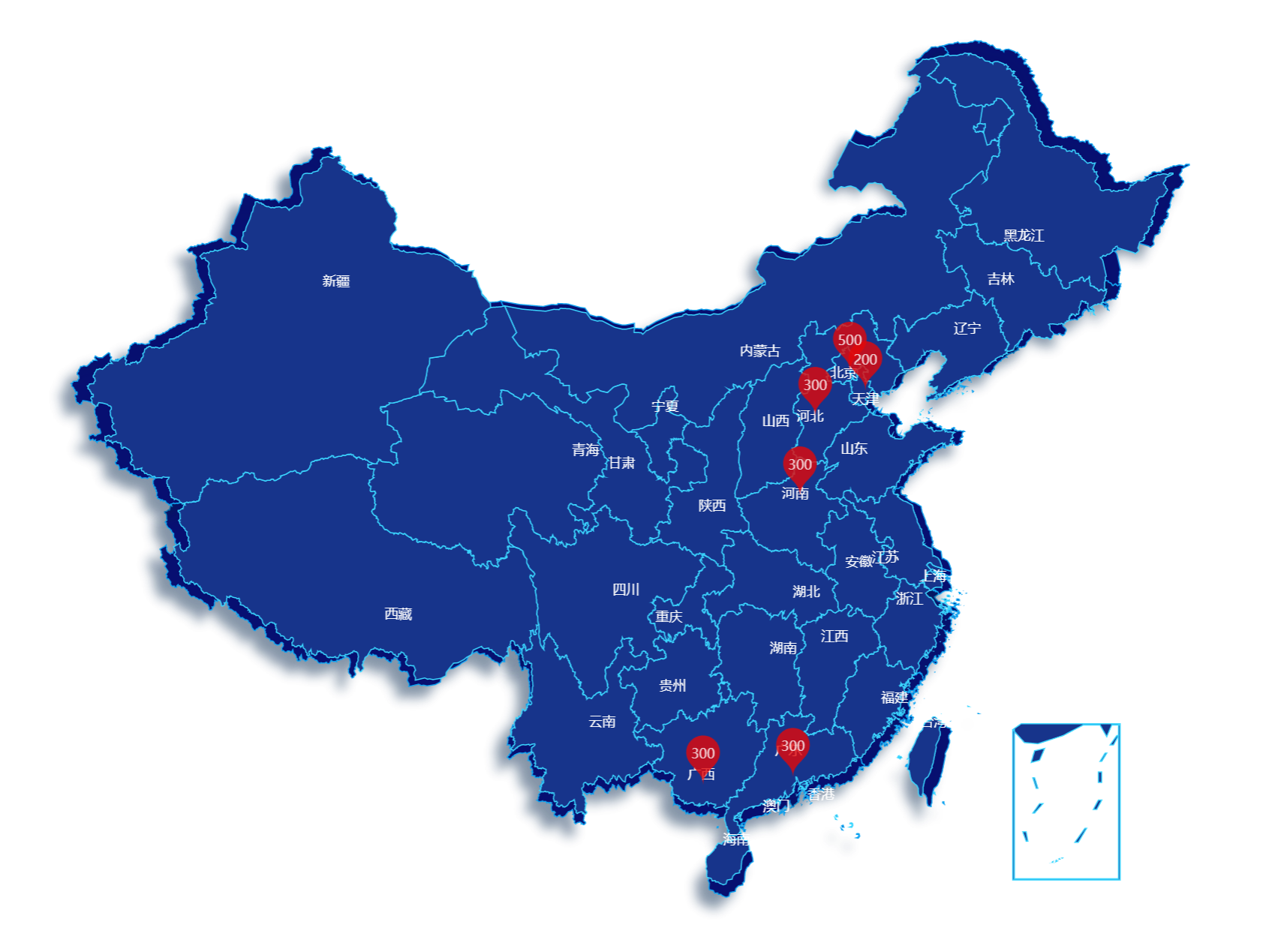
例子:
当 x = 0 x = 0 x=0时 f(x) = 1,当 x ≠ 0 x \ne 0 x=0时, f ( x ) = sin x x f(x) = \frac{\sin x}{x} f(x)=xsinx, 求f’'(x)。
解:
二阶导数是导数的导数,按照定义为:
f ′ ′ ( x ) = lim x → 0 f ′ ( x + Δ x ) − f ′ ( x ) Δ x f''(x) = \lim _{x \to 0}\frac{f'(x+\Delta x) - f'(x)}{\Delta x} f′′(x)=x→0limΔxf′(x+Δx)−f′(x)
而f’(x)在x=0和 x ≠ 0 x \ne 0 x=0时虽然都趋近于0,但是他们是不同的。
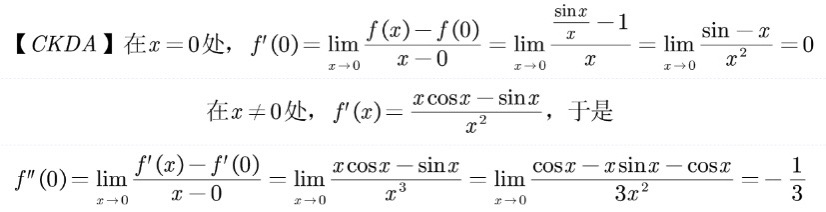



![2023年中国档案信息化发展历程、竞争格局及行业市场规模分析[图]](https://img-blog.csdnimg.cn/img_convert/1fc33ac4d7ceef06b47bff07424e9e4f.png)