1.React Router的基本使用
安装:安装时,选择react-router-dom,react-router会包含一些react-native的内容,web开发并不需要;
npm install react-router-dom
路径模式
- BrowserRouter使用history模式;
-
HashRouter 使用hash模式;
路由映射配置
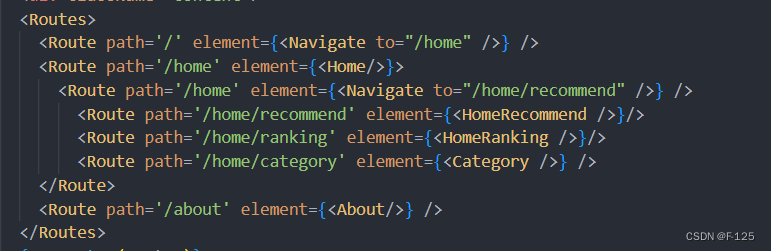
Routes:包裹所有的Route,在其中匹配一个路由;
Route:Route用于路径的匹配;
- path属性:用于设置匹配到的路径;
-
element 属性:设置匹配到路径后,渲染的组件;
路由配置和跳转
Link和NavLink:
- 通常路径的跳转是使用Link组件,最终会被渲染成a元素;
- NavLink是在Link基础之上增加了一些样式属性;
-
to属性:Link中最重要的属性,用于设置跳转到的路径;

Navigate导航
Navigate
用于路由的重定向,当这个组件出现时,就会执行跳转到对应的to路径中;
Navigate是由react-router-dom提供的组件, 可直接调用;
路由参数传递
- 动态路由的方式;
-
search传递参数;
动态路由的概念指的是路由中的路径并不会固定:
- 比如/detail的path对应一个组件Detail;
-
将path在Route匹配时写成/detail/:id,那么 /detail/abc、/detail/123都可以匹配到该Route,并且进行显示,该匹配规则及称之为动态路由;
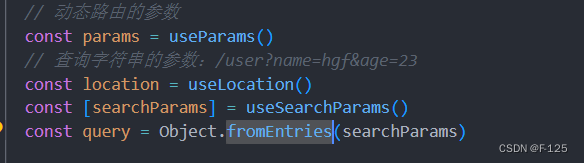
动态路由参数获取通过
useParams函数获取,useParams由react-router-dom库提供的api;
search参数获取:
通过useSearchParams函数获取,useSearchParams由react-router-dom库提供的api,该函数返回一个entries对象,通过Object.fromEntries转换成普通对象即可;
路由的配置文件
目前我们所有的路由定义都是直接使用Route组件,并且添加属性来完成的,但是这样的方式会让路由变得非常混乱,早期的时候,
Router
并且没有提供相关的
API
,我们需要借助于
react-router-config完成,在Router6.x中,react-router-dom库
提供了useRoutesAPI可以集中路由配置到一个文件中管理。
router.js
import { Navigate } from "react-router-dom"
import Home from "../pages/Home"
import HomeRecommend from "../pages/HomeRecommend"
import HomeRanking from "../pages/HomeRanking"
// import Category from "../pages/Category"
// import About from "../pages/About"
import React from "react"
const Category = React.lazy(() => import('../pages/Category'))
const About = React.lazy(() => import('../pages/About'))
const Routes = [
{
path: '/',
element: <Navigate to='/home' />
},
{
path: '/home',
element: <Home/>,
children: [
{
path: '/home/recommend',
element: <HomeRecommend />
},
{
path: '/home/ranking',
element: <HomeRanking />
},
{
path: '/home/category',
element: <Category />
}
]
},
{
path: '/about',
element: <About />
}
]
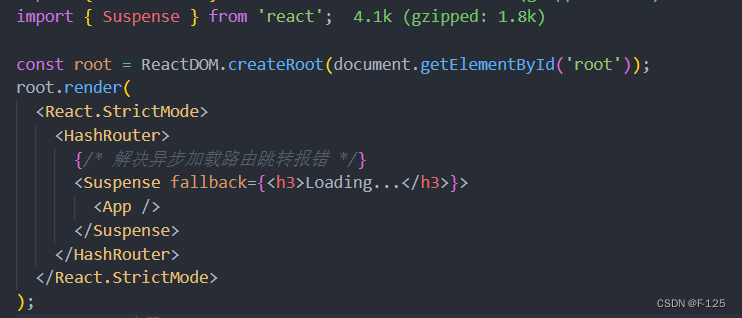
export default Routes组件中使用
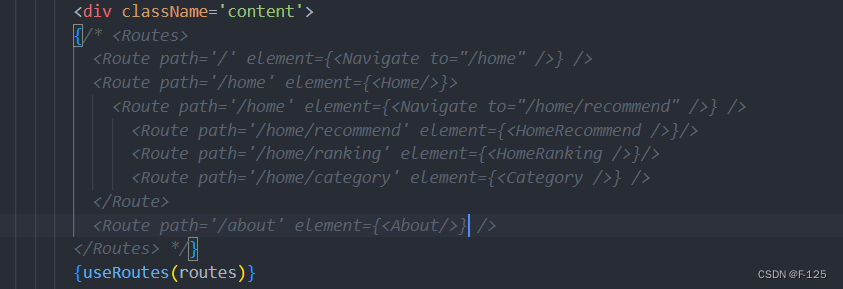
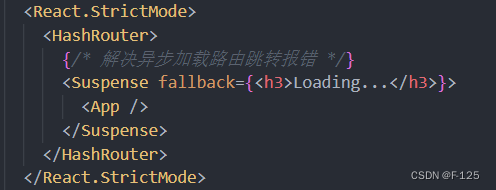
如果我们对某些组件进行了异步加载(懒加载),那么需要使用Suspense进行包裹: