前言:
据说著名犹太历史学家Josephus有过如下故事:
在罗马人占领乔塔帕特后,39个犹太人和Josephus及他的朋友躲进一个洞里,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈。
由第一个人开始报数,报数到3的人就自杀,再由下一个人重新报1,报数到3的人就自杀,这样依次下去,知道剩下最后一个人时,那个人可以自由选择自己的命运。
这就是著名的约瑟夫问题。现在请用单向链表描述该结构并呈现整个自杀过程。

目录
题目:
示例:
图例:
题目解析:
约瑟夫问题的本质:
图例:
删除节点:
未删除,继续报数:
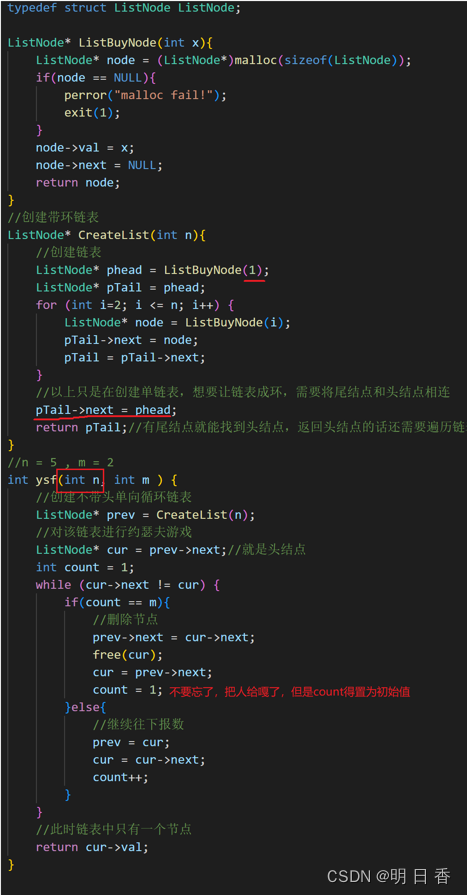
代码演示:

题目:
编号为1到n的n 个人围成一圈。从编号为 1 的人开始报数,报到 m 的人离开,下一个人继续从 1开始报数。
n-1 轮结束以后,只剩下一个人,问最后留下的这个人编号是多少?

示例:
- 输入: 5 , 2
- 返回值: 3
说明 :
- 开始 5 个 人 他们的编号分别是 :1,2,3,4,5
- 从1开始报数,1->1,2->2 编号为2的人离开
- 剩下:1,3,4,5,从3开始报数,3->1,4->2编号为4的人离开
- 剩下:1,3,5,从5开始报数,5->1,1->2编号为1的人离开
- 剩下:3,5,从3开始报敷,3->1,5->2编号为5的人离开
- 最后留下人的编号是3
图例:
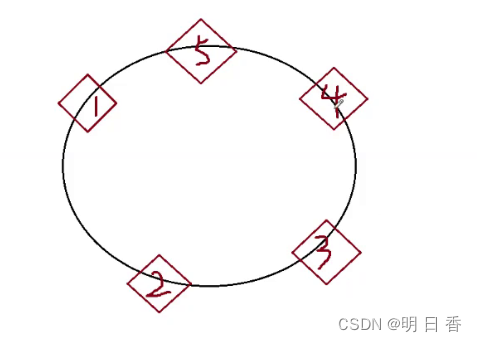
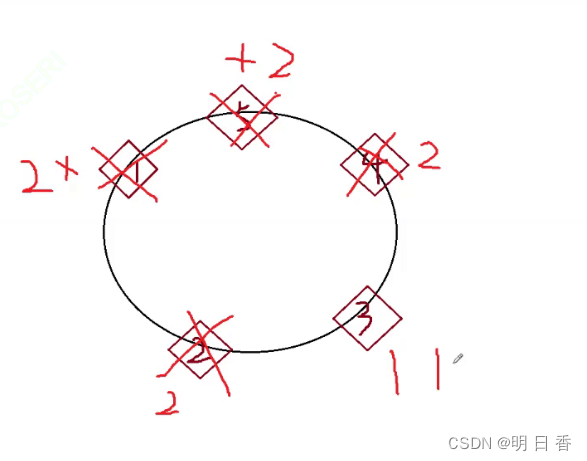
- 通过图例和题目要求,让我们想到了一种链表,带环链表。
- 带环链表之所以叫带环链表,是因为最后面的节点内的指针指向了头节点,也就是头尾相连了。
- 且,带环链表的创建和单链表的创建是一样的,只不过带环链表多了一步,尾节点的指针 next 指向了头节点。

题目解析:
- 首先,因为题目的要求,需要拥有两个数,一个是指定的次数,一个是节点的个数。
![]()
- 其次,我们要创建链表的节点,而创造链表的节点需要开辟空间,这里需要使用malloc函数,并将开辟的空间交予头节点指针,以此形成第一个节点。
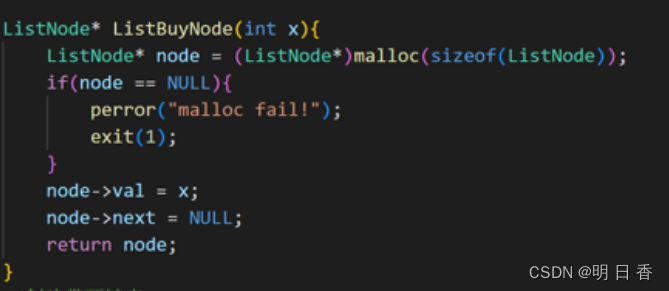
- 在进行开辟空间后,需要形成链表,而链表中,节点的个数和之前的输入值有关,所以需要进行循环创建节点,对此要和上面开辟节点的函数形成调用联动。
- 而且,为了使得变成一个环形链表,我们需要在所有节点开辟后,并形成单链表的最后,将链表的最后一个节点内部的指针指向头节点。
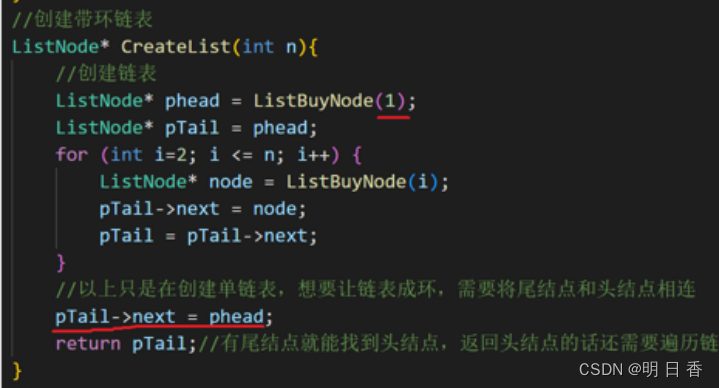
- 在形成节点后我们则进入约瑟夫问题。

约瑟夫问题的本质:
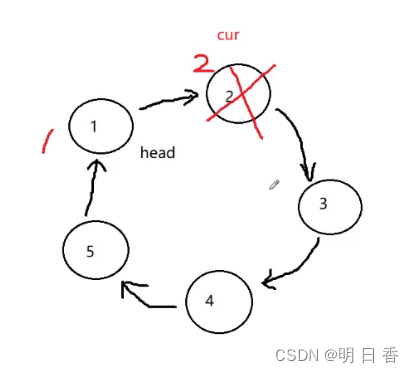
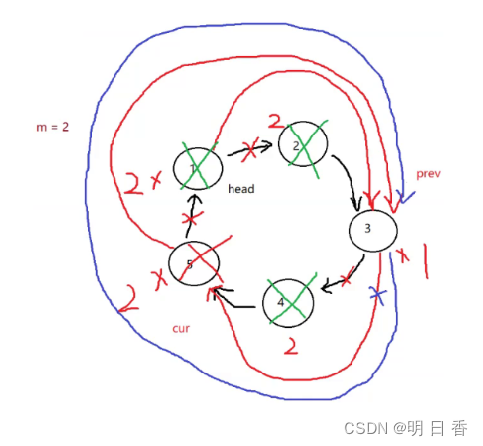
如上图所示,我们可以知道,约瑟夫问题的本质实际上就是删除指定位置的节点。
而对于删除指定位置的节点,我们需要两个指针进行遍历解决。
链表——单链表的简单介绍-CSDN博客
https://blog.csdn.net/2301_76445610/article/details/133811446?spm=1001.2014.3001.5501
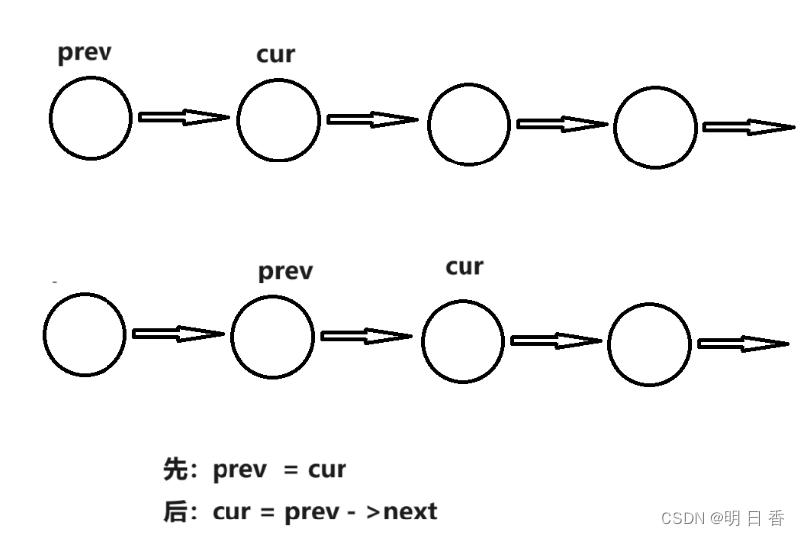
两个指针:一个是通过遍历访问指定位置(cur),一个是通过遍历访问到指定位置的前一个节点(prev)。
而又如图所示,当最后只剩下一个链表的时候,那一个遍历指定位置的指针指向的节点,该节点内部的指针指向的是它自己。
所以当遍历指定位置 的节点 的内部指针 指向它自己的时候,就是跳出约瑟夫游戏判断的时候。

- 因为之前返回值是返回环形指针的最后一个尾节点(原单链表尾节点),所有prev是尾节点,而prev->next 则是原单链表的头节点。
![]()
- 而因为我们是从头指针开始的约瑟夫问题的,所以报数是从1开始的,这里我们就需要一个计数(报数)变量。
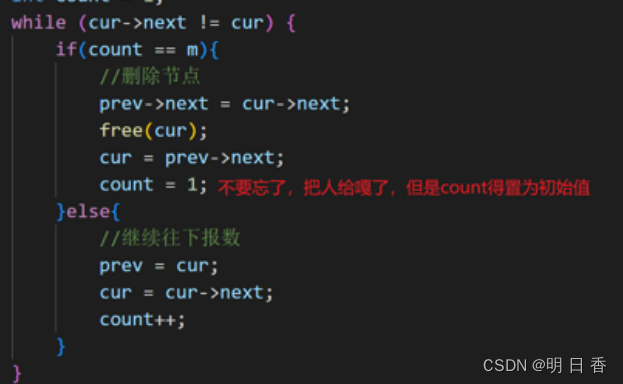
- 而接下来,关于约瑟夫问题的核心部分,便是计数和删除节点。
- 当计数变量抵达我们指定的数字后,需要将节点进行删除,进行修改节点内部指针指向,且将计数变量重置回初始值(重置回1),而未抵达我们指定的数字时,则继续进行计数。
图例:
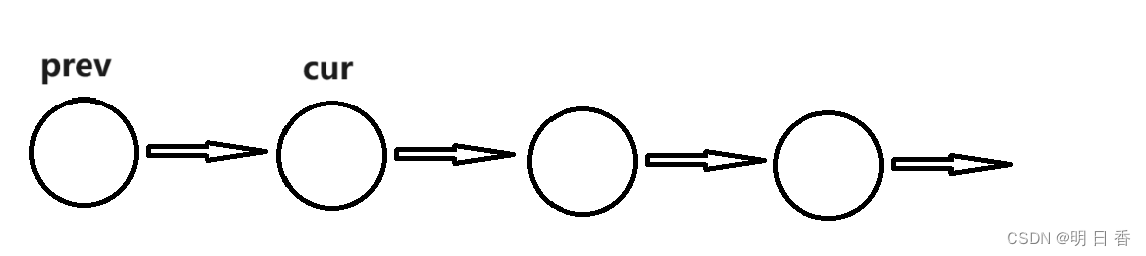
删除节点:
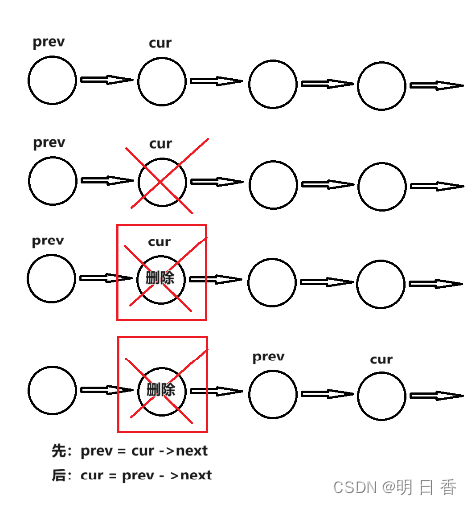
未删除,继续报数:
代码演示: