文章目录
- 1、导数的概念
- 1.1、引例
- 1.1.1、变速直线运动瞬时速度
- 1.1.2、曲线的切线
- 1.2、导数的定义
- 1.3、证明常用导数
- 1.4、导数的几何意义
- 1.5、可导与连续的关系
- 2、函数的求导法则
- 2.1、函数的和、差、积、商的求导法则
- 2.2、反函数的求导法则
- 2.3、复合函数的求导法则
- 2.4、基本初等函数的导数公式
- 3、高阶导数
- 3.1、高阶导数的公式
- 4、隐函数和参数方程确定的函数的导数
- 4.1、隐函数的导数
- 4.2、由参数方程所确定的函数的导数
- 4.3、相关变化率
- 5、函数的微分
- 5.1、引例
- 5.2、定义
- 5.3、可微与可导
- 5.4、微分的几何意义
- 5.5、微分的运算法则

1、导数的概念
1.1、引例
1.1.1、变速直线运动瞬时速度
这个问题描述的是,假设有一个物品从
a
a
a时刻一直运动到
b
b
b时刻,如何刻画它在
(
a
,
b
)
(a,b)
(a,b)上的某一点的速度呢?
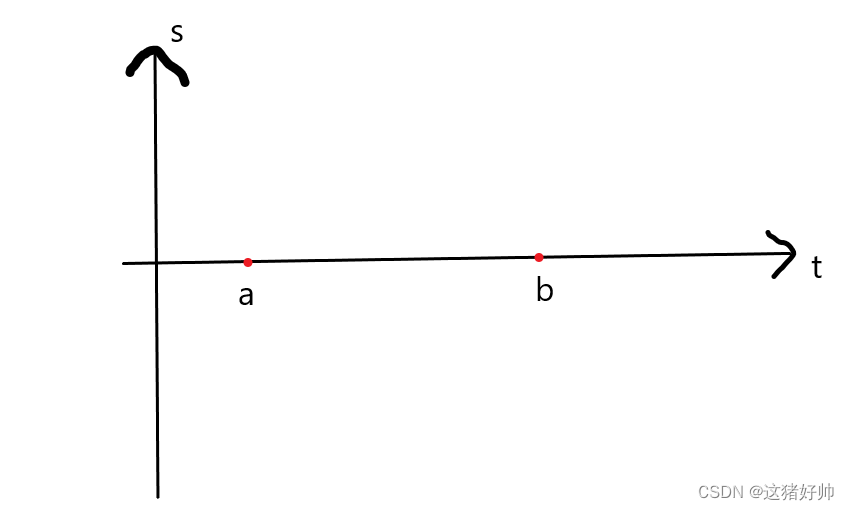
s = f ( t ) s = f(t) s=f(t)
第一种情况:匀速
如果是匀速直线运动的话,即我们算出这一段路程的位移,再算出它的时间,两个相除即为速度
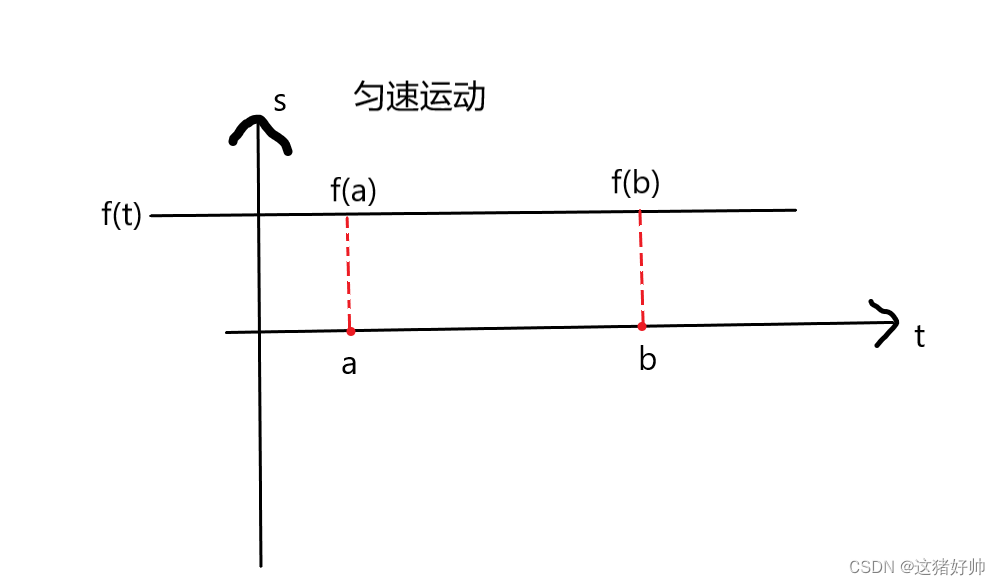
v = f ( b ) − f ( a ) b − a v=\frac{f(b)-f(a)}{b-a} v=b−af(b)−f(a)
第二种情况:变速
变速运动我们想要看某一点上的瞬时速度,尝试能不能转化为第一种匀速的情况呢?
如果我们想看一点
t
0
t_0
t0的瞬时速度,那么我们就想到取一个
Δ
t
\Delta t
Δt,如果这个
Δ
t
\Delta t
Δt足够小,
t
0
+
Δ
t
t_0+\Delta t
t0+Δt的变化肯定小,那么它的速度变化也肯定是比较小的,也就近似可以看成是一段匀速运动

当
t
0
t_0
t0与
t
0
+
Δ
t
t_0+\Delta t
t0+Δt非常接近时,近似一个匀速运动,匀速运动的平均速度即为:
f
(
t
0
+
Δ
x
)
−
f
(
t
0
)
Δ
x
=
平均速度
≈
瞬时速度
\frac{f(t_0+\Delta x)-f(t_0)}{\Delta x}=平均速度\approx 瞬时速度
Δxf(t0+Δx)−f(t0)=平均速度≈瞬时速度
而上面的接近过程就可以用极限来表示:
lim
Δ
t
→
0
f
(
t
0
+
Δ
t
)
−
f
(
t
0
)
Δ
t
\lim_{\Delta t \to 0}\frac{f(t_0+\Delta t)-f(t_0)}{\Delta t}
Δt→0limΔtf(t0+Δt)−f(t0)
此时平均速度就转化为了
t
0
t_0
t0这一点的瞬时速度
1.1.2、曲线的切线
f
(
x
)
f(x)
f(x)上有两点
(
x
0
,
f
(
x
0
)
)
,
(
x
0
+
Δ
x
,
f
(
x
0
+
Δ
x
)
)
,
(x_0,f(x_0)),(x_0+\Delta x,f(x_0+\Delta x)),
(x0,f(x0)),(x0+Δx,f(x0+Δx)),过这两点做一条直线,记为割线
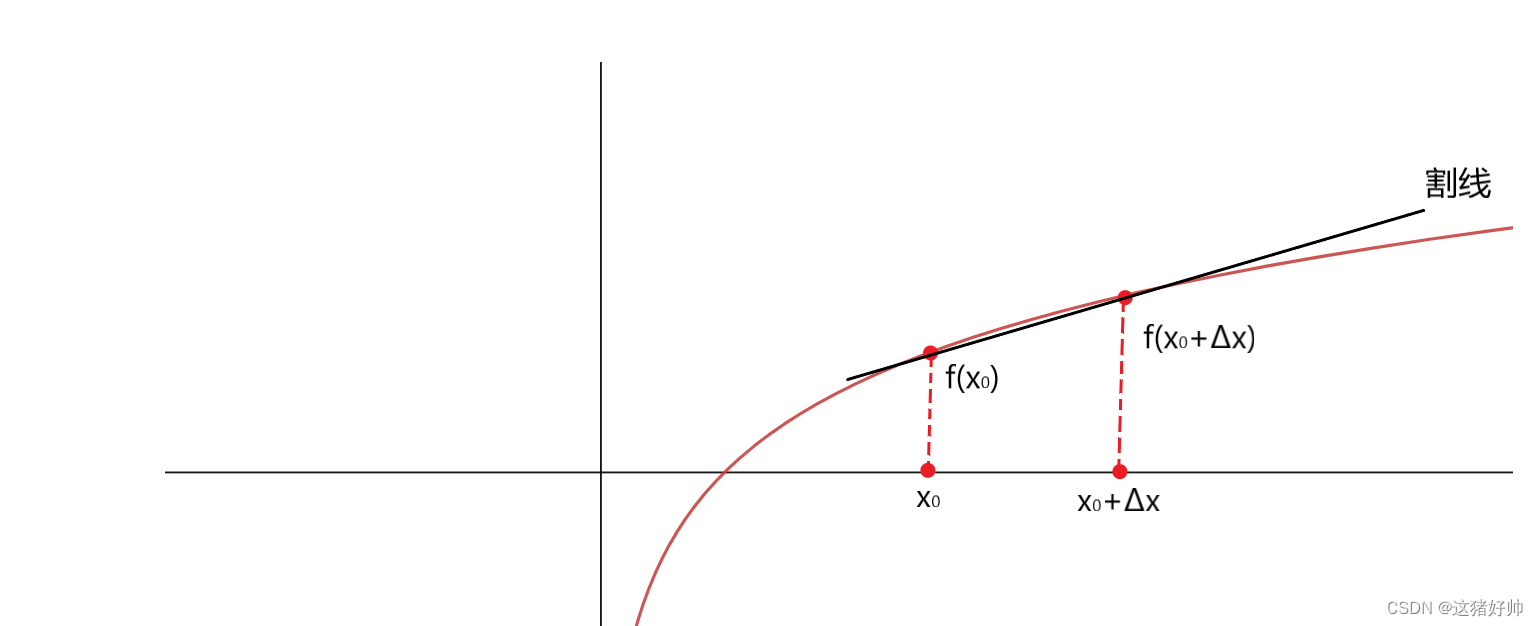
割线的斜率
k
割
=
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
k_割=\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}
k割=Δxf(x0+Δx)−f(x0)
而当
x
0
+
Δ
x
与
x
0
x_0+\Delta x与x_0
x0+Δx与x0无限接近时按照做割线的方法再做一条线,即割线的极限,记为切线
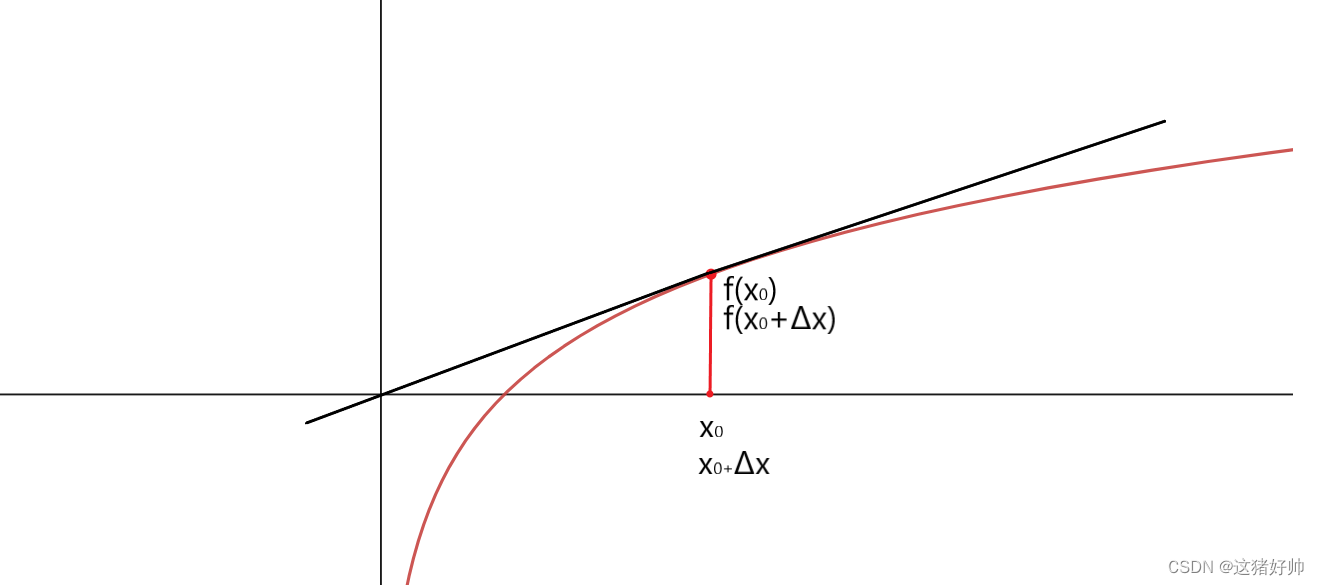
而既然割线的斜率我们知道怎么求,那自然切线的斜率也就出来了,只要取一个极限即可
k 切 = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x k_切=\lim_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} k切=limΔx→0Δxf(x0+Δx)−f(x0)
1.2、导数的定义
定义:若
lim
Δ
x
→
0
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
\lim_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}
limΔx→0Δxf(x0+Δx)−f(x0)存在
则称
f
(
x
)
f(x)
f(x)在
x
0
x_0
x0点可导,记作:
f
′
(
x
)
=
y
′
∣
x
=
x
0
=
d
y
d
x
∣
x
=
x
0
f^\prime(x)=y\prime|_{x = x_0}=\frac{dy}{dx}|_{x = x_0}
f′(x)=y′∣x=x0=dxdy∣x=x0
f
′
(
x
0
)
=
lim
Δ
x
→
0
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
=
lim
x
→
x
0
f
(
x
)
−
f
(
x
0
)
x
−
x
0
=
lim
Δ
x
→
0
Δ
y
Δ
x
f^\prime(x_0)=\lim_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\lim_{x \to x_0}\frac{f(x)-f(x_0)}{x - x_0}=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}
f′(x0)=Δx→0limΔxf(x0+Δx)−f(x0)=x→x0limx−x0f(x)−f(x0)=Δx→0limΔxΔy
若以上极限不存在,则称
f
(
x
)
f(x)
f(x)在
x
0
x_0
x0处不可导
若极限为无穷大,则称
f
(
x
)
f(x)
f(x)在
x
0
x_0
x0处导数为无穷大
左导数定义: f − ′ ( x 0 ) = lim Δ x → 0 − f ( x 0 + Δ x ) − f ( x 0 ) Δ x = lim x → x 0 − f ( x ) − f ( x 0 ) x − x 0 f^\prime_-(x_0)=\lim_{\Delta x \to 0^-}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\lim_{x \to x_0^-}\frac{f(x)-f(x_0)}{x - x_0} f−′(x0)=Δx→0−limΔxf(x0+Δx)−f(x0)=x→x0−limx−x0f(x)−f(x0)
右导数定义: f + ′ ( x 0 ) = lim Δ x → 0 + f ( x 0 + Δ x ) − f ( x 0 ) Δ x = lim x → x 0 + f ( x ) − f ( x 0 ) x − x 0 f^\prime_+(x_0)=\lim_{\Delta x \to 0^+}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\lim_{x \to x_0^+}\frac{f(x)-f(x_0)}{x - x_0} f+′(x0)=Δx→0+limΔxf(x0+Δx)−f(x0)=x→x0+limx−x0f(x)−f(x0)
左右导数与导数的关系:可导 ⇚ ⇛ \Lleftarrow\Rrightarrow ⇚⇛左右导数存在且相等
区间上可导:
1、若
f
(
x
)
f(x)
f(x)开区间
(
a
,
b
)
(a,b)
(a,b)上每一点都可导,而每一点的函数值形成的新函数我们称为导函数,记为
f
′
(
x
)
,
x
∈
(
a
,
b
)
f^\prime(x),x\in(a,b)
f′(x),x∈(a,b)
2、若上述区间为闭区间
[
a
,
b
]
[a,b]
[a,b],那么不仅要求区间内每点可导,而且还要求端点
a
a
a右可导,端点
b
b
b左可导
1.3、证明常用导数
(1)、 ( x α ) ′ = a x α − 1 ( x > 0 ) (x^\alpha)^\prime = ax^{\alpha-1}(x >0) (xα)′=axα−1(x>0)
【证明】
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
=
(
x
+
Δ
x
)
α
−
x
α
Δ
x
\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}=\frac{(x+\Delta x)^\alpha-x^\alpha}{\Delta x}
limΔx→0Δxf(x+Δx)−f(x)=Δx(x+Δx)α−xα
=
x
α
[
(
1
+
Δ
x
x
)
α
−
1
]
Δ
x
=
x
α
α
Δ
x
x
Δ
x
=
α
x
α
−
1
=\frac{x^\alpha[(1+\frac{\Delta x}{x})^\alpha-1]}{\Delta x}=\frac{x^\alpha\alpha\frac{\Delta x}{x}}{\Delta x}=\alpha x^{\alpha -1}
=Δxxα[(1+xΔx)α−1]=ΔxxααxΔx=αxα−1
(2)、 ( a x ) ′ = a x ln a ( a > 0 , a ≠ 1 ) (a^x)^\prime=a^x\ln a (a>0,a≠1) (ax)′=axlna(a>0,a=1)
【证明】
由
lim
x
→
0
a
x
−
1
∼
x
ln
a
\lim_{x \to 0}a^x-1\sim x\ln a
limx→0ax−1∼xlna
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
=
lim
Δ
x
→
0
a
x
+
Δ
x
−
a
x
Δ
x
=
lim
Δ
x
→
0
a
x
[
a
Δ
x
−
1
]
Δ
x
=
lim
Δ
x
→
0
a
x
Δ
x
ln
a
Δ
x
=
a
x
ln
a
\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}=\lim_{\Delta x \to 0}\frac{a^{x+\Delta x}-a^x}{\Delta x}=\lim_{\Delta x \to 0}\frac{a^x[a^{\Delta x}-1]}{\Delta x}=\lim_{\Delta x \to 0}\frac{a^x\Delta x\ln a}{\Delta x}=a^x\ln a
limΔx→0Δxf(x+Δx)−f(x)=limΔx→0Δxax+Δx−ax=limΔx→0Δxax[aΔx−1]=limΔx→0ΔxaxΔxlna=axlna
(3)、 ( log a x ) ′ = 1 x ln a ( a > 0 , a ≠ 1 ) (\log_ax)^\prime=\frac{1}{x\ln a}(a>0,a≠1) (logax)′=xlna1(a>0,a=1)
【证明】
由
lim
x
→
0
log
a
(
1
+
x
)
∼
x
ln
a
\lim_{x \to 0}\log_a(1+x)\sim x\ln a
limx→0loga(1+x)∼xlna
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
=
lim
Δ
x
→
0
log
a
(
x
+
Δ
x
)
−
log
a
x
Δ
x
=
lim
Δ
x
→
0
log
a
(
1
+
Δ
x
x
)
Δ
x
=
lim
Δ
x
→
0
Δ
x
x
ln
x
Δ
x
=
1
x
ln
x
\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}=\lim_{\Delta x \to 0}\frac{\log_a(x+\Delta x)-\log_a{x}}{\Delta x}=\lim_{\Delta x \to 0}\frac{\log_a(1+\frac{\Delta x}{x})}{\Delta x}=\lim_{\Delta x \to 0}\frac{\frac{\Delta x}{x\ln x}}{\Delta x}=\frac{1}{x\ln x}
limΔx→0Δxf(x+Δx)−f(x)=limΔx→0Δxloga(x+Δx)−logax=limΔx→0Δxloga(1+xΔx)=limΔx→0ΔxxlnxΔx=xlnx1
(4)、 ( sin x ) ′ = cos x (\sin x)^\prime=\cos x (sinx)′=cosx
【证明】
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
=
sin
(
x
+
Δ
x
)
−
sin
x
Δ
x
=
2
sin
(
Δ
x
2
)
×
cos
(
2
x
+
Δ
x
2
)
Δ
x
=
2
Δ
x
2
cos
(
2
x
+
Δ
x
2
)
Δ
x
=
cos
x
\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}=\frac{\sin(x+\Delta x)-\sin x}{\Delta x}=\frac{2\sin(\frac{\Delta x}{2})\times \cos(\frac{2x+\Delta x}{2})}{\Delta x}=\frac{2\frac{\Delta x}{2}\cos(\frac{2x+\Delta x}{2})}{\Delta x}=\cos x
limΔx→0Δxf(x+Δx)−f(x)=Δxsin(x+Δx)−sinx=Δx2sin(2Δx)×cos(22x+Δx)=Δx22Δxcos(22x+Δx)=cosx
(5)、 ( cos x ) ′ = − sin x (\cos x)^\prime=-\sin x (cosx)′=−sinx
【证明】
lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x = cos ( x + Δ x ) − cos x Δ x = − 2 sin ( 2 x + Δ x 2 ) sin ( Δ x 2 ) Δ x = − 2 Δ x 2 sin ( 2 x + Δ x 2 ) Δ x = − sin x \lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}=\frac{\cos(x+\Delta x)-\cos x}{\Delta x}=\frac{-2\sin(\frac{2x+\Delta x}{2})\sin(\frac{\Delta x}{2})}{\Delta x}=\frac{-2\frac{\Delta x}{2}\sin(\frac{2x+\Delta x}{2})}{\Delta x}=-\sin x limΔx→0Δxf(x+Δx)−f(x)=Δxcos(x+Δx)−cosx=Δx−2sin(22x+Δx)sin(2Δx)=Δx−22Δxsin(22x+Δx)=−sinx
1.4、导数的几何意义
在引例中,我们详细说过导数的几何意义
导数
f
′
(
x
0
)
f^\prime(x_0)
f′(x0)在几何上表示曲线
y
=
f
(
x
)
y=f(x)
y=f(x)在点
(
x
0
,
f
(
x
0
)
)
(x_0,f(x_0))
(x0,f(x0))处切线的斜率
切线方程:
y
−
y
0
=
f
′
(
x
0
)
(
x
−
x
0
)
y-y_0=f^\prime(x_0)(x-x_0)
y−y0=f′(x0)(x−x0)
法线方程:
y
−
y
0
=
−
1
f
′
(
x
0
)
(
x
−
x
0
)
y-y_0 = -\frac{1}{f^\prime(x_0)}(x-x_0)
y−y0=−f′(x0)1(x−x0)
1.5、可导与连续的关系
可导 ⇛ ⇛ ⇛ 连续
【证明】
即证:
lim
Δ
x
→
0
Δ
y
=
0
\lim_{Δ x → 0}Δ y=0
limΔx→0Δy=0
∵
Δ
y
=
Δ
y
Δ
x
Δ
x
∵Δ y=\frac{Δ y}{Δ x}Δ x
∵Δy=ΔxΔyΔx
∵
Δ
y
Δ
x
→
0
,
Δ
x
→
0
∵\frac{Δ y}{Δ x}\to 0,Δ x→0
∵ΔxΔy→0,Δx→0
∴
lim
Δ
x
→
0
Δ
y
=
0
∴\lim_{Δ x\to0}Δ y=0
∴limΔx→0Δy=0
证毕
注意:连续无法推出可导
例如:
1、
y
=
∣
x
∣
y=|x|
y=∣x∣在
x
=
0
x=0
x=0处虽然连续,并且左右导数都存在,但它的左右导数并不相等,故不可导
2、
y
=
x
1
3
y=x^\frac{1}{3}
y=x31在
x
=
0
x=0
x=0处虽然连续,并且也有一条切线y轴,但它的导数是无穷大,故也不可导
3、
y
=
{
x
sin
1
x
x
≠
0
0
,
x
=
0
y=\begin{cases} x\sin\frac{1}{x} & x≠0 \\ 0, & x=0 \\ \end{cases}
y={xsinx10,x=0x=0,虽然这个函数连续,但左右导数都不存在,故不可导
2、函数的求导法则
2.1、函数的和、差、积、商的求导法则
定理1、设
u
(
x
)
,
v
(
x
)
u(x),v(x)
u(x),v(x)都可导,则
1、
(
u
±
v
)
′
=
u
′
±
v
′
(u ± v)^′=u^′±v^′
(u±v)′=u′±v′
2、
(
u
v
)
′
=
u
′
v
+
u
v
′
(uv)^′=u^′v+uv^′
(uv)′=u′v+uv′
3、
(
u
v
)
′
=
u
′
v
−
v
′
u
v
2
(
v
≠
0
)
(\frac{u}{v})^′=\frac{u^′v-v^′u}{v^2}(v≠0)
(vu)′=v2u′v−v′u(v=0)
【证明:
(
u
+
v
)
′
=
u
′
+
v
′
(u+v)^′=u^′+v^′
(u+v)′=u′+v′】
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
=
u
(
x
+
Δ
x
)
+
v
(
x
+
Δ
x
)
−
u
(
x
)
−
v
(
x
)
Δ
x
\frac{f(x+Δx)-f(x)}{Δx}=\frac{u(x+Δx)+v(x+Δx)-u(x)-v(x)}{Δx}
Δxf(x+Δx)−f(x)=Δxu(x+Δx)+v(x+Δx)−u(x)−v(x)
故:
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
=
lim
Δ
x
→
0
u
(
x
+
Δ
x
)
−
u
(
x
)
Δ
x
+
lim
Δ
x
→
0
v
(
x
+
Δ
x
)
−
v
(
x
)
Δ
x
=
u
′
+
v
′
\lim_{Δx→0}\frac{f(x+Δx)−f(x)}{Δx}=\lim_{Δx→0}\frac{u(x+Δx)-u(x)}{Δx}+\lim_{Δx→0}\frac{v(x+Δx)-v(x)}{Δx}=u^′+v^′
limΔx→0Δxf(x+Δx)−f(x)=limΔx→0Δxu(x+Δx)−u(x)+limΔx→0Δxv(x+Δx)−v(x)=u′+v′
证毕
【证明:
(
u
v
)
′
=
u
′
v
+
u
v
′
(uv)^′=u^′v+uv^′
(uv)′=u′v+uv′】
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
=
u
(
x
+
Δ
x
)
v
(
x
+
Δ
x
)
−
u
(
x
)
v
(
x
)
Δ
x
\frac{f(x+Δx)-f(x)}{Δx}=\frac{u(x+Δx)v(x+Δx)-u(x)v(x)}{Δx}
Δxf(x+Δx)−f(x)=Δxu(x+Δx)v(x+Δx)−u(x)v(x)
=
u
(
x
+
Δ
x
)
v
(
x
+
Δ
x
)
−
u
(
x
)
v
(
x
+
Δ
x
)
+
u
(
x
)
v
(
x
+
Δ
x
)
−
u
(
x
)
v
(
x
)
Δ
x
=\frac{u(x+Δx)v(x+Δx)-u(x)v(x+Δx)+u(x)v(x+Δx)-u(x)v(x)}{Δx}
=Δxu(x+Δx)v(x+Δx)−u(x)v(x+Δx)+u(x)v(x+Δx)−u(x)v(x)
故:
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
=
lim
Δ
x
→
0
u
(
x
+
Δ
x
)
v
(
x
+
Δ
x
)
−
u
(
x
)
v
(
x
+
Δ
x
)
Δ
x
+
lim
Δ
x
→
0
u
(
x
)
v
(
x
+
Δ
x
)
−
u
(
x
)
v
(
x
)
Δ
x
\lim_{Δx→0}\frac{ f(x+Δx)−f(x) }{Δx}=\lim_{Δx→0}\frac{u(x+Δx)v(x+Δx)−u(x)v(x+Δx)}{Δx}+\lim_{Δx→0}\frac{u(x)v(x+Δx)−u(x)v(x)}{Δx}
limΔx→0Δxf(x+Δx)−f(x)=limΔx→0Δxu(x+Δx)v(x+Δx)−u(x)v(x+Δx)+limΔx→0Δxu(x)v(x+Δx)−u(x)v(x)
=
u
′
v
+
u
v
′
=u^′v+uv^′
=u′v+uv′
证毕
【证明:
(
u
v
)
′
=
u
′
v
−
v
′
u
v
2
(
v
≠
0
)
(\frac{u}{v})^′=\frac{u^′v-v^′u}{v^2}(v≠0)
(vu)′=v2u′v−v′u(v=0)】
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
=
u
(
x
+
Δ
x
)
v
(
x
+
Δ
x
)
−
u
(
x
)
v
(
x
)
Δ
x
=
u
(
x
+
Δ
x
)
v
(
x
)
−
u
(
x
)
v
(
x
+
Δ
x
)
v
(
x
+
Δ
x
)
v
(
x
)
Δ
x
\frac{f(x+Δx)-f(x)}{Δx}=\frac{\frac{u(x+Δx)}{v(x+Δx)}-\frac{u(x)}{v(x)}}{Δx}=\frac{u(x+Δx)v(x)-u(x)v(x+Δx)}{v(x+Δx)v(x)Δx}
Δxf(x+Δx)−f(x)=Δxv(x+Δx)u(x+Δx)−v(x)u(x)=v(x+Δx)v(x)Δxu(x+Δx)v(x)−u(x)v(x+Δx)
=
u
(
x
+
Δ
x
)
v
(
x
)
−
u
(
x
)
v
(
x
)
+
u
(
x
)
v
(
x
)
−
u
(
x
)
v
(
x
+
Δ
x
)
v
(
x
+
Δ
x
)
v
(
x
)
Δ
x
=\frac{u(x+Δx)v(x)-u(x)v(x)+u(x)v(x)-u(x)v(x+Δx)}{v(x+Δx)v(x)Δx}
=v(x+Δx)v(x)Δxu(x+Δx)v(x)−u(x)v(x)+u(x)v(x)−u(x)v(x+Δx)
即:
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
=
lim
Δ
x
→
0
u
(
x
+
Δ
x
)
v
(
x
)
−
u
(
x
)
v
(
x
)
+
u
(
x
)
v
(
x
)
−
u
(
x
)
v
(
x
+
Δ
x
)
v
(
x
+
Δ
x
)
v
(
x
)
Δ
x
=
u
′
v
−
u
v
′
v
2
\lim_{Δx →0}\frac{f(x+Δx)-f(x)}{Δx}=\lim_{Δx \to 0}\frac{u(x+Δx)v(x)-u(x)v(x)+u(x)v(x)-u(x)v(x+Δx)}{v(x+Δx)v(x)Δx}=\frac{u^′v-uv^′}{v^2}
limΔx→0Δxf(x+Δx)−f(x)=limΔx→0v(x+Δx)v(x)Δxu(x+Δx)v(x)−u(x)v(x)+u(x)v(x)−u(x)v(x+Δx)=v2u′v−uv′
证毕
2.2、反函数的求导法则
定理:设区间
I
I
I上严格单调且连续的函数
x
=
f
(
y
)
x=f(y)
x=f(y)在
y
y
y处可导,且
f
′
(
y
)
≠
0
,
f^′(y)≠0,
f′(y)=0,则它的反函数
y
=
f
−
1
(
x
)
y=f^{-1}(x)
y=f−1(x)在对应点可导,且
(
f
−
1
)
′
(
x
)
=
1
f
′
(
y
)
,
d
y
d
x
=
1
d
x
d
y
(f^{-1})^′(x)=\frac{1}{f^′(y)},\frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}
(f−1)′(x)=f′(y)1,dxdy=dydx1
注意:严格单调且连续是为了保证一定有反函数
1
、
(
arcsin
x
)
′
=
1
1
−
x
2
1、(\arcsin x)^′ = \frac{1}{\sqrt{1-x^2}}
1、(arcsinx)′=1−x21
2
、
(
arccos
x
)
′
=
−
1
1
−
x
2
2、(\arccos x)^′=-\frac{1}{\sqrt{1-x^2}}
2、(arccosx)′=−1−x21
3
、
(
arctan
x
)
′
=
1
1
+
x
2
3、(\arctan x)^′=\frac{1}{1+x^2}
3、(arctanx)′=1+x21
4
、
(
a
r
c
c
o
t
x
)
′
=
−
1
1
+
x
2
4、(arccot\ x)^′=-\frac{1}{1+x^2}
4、(arccot x)′=−1+x21
【证明
(
arcsin
x
)
′
=
1
1
−
x
2
(\arcsin x)^′ = \frac{1}{\sqrt{1-x^2}}
(arcsinx)′=1−x21】
y
=
arcsin
x
y = \arcsin x
y=arcsinx 的反函数为
x
=
sin
y
x=\sin y
x=siny
根据反函数的求导反则:
(
arcsin
x
)
′
=
1
(
sin
y
)
′
=
1
cos
y
=
1
1
−
sin
2
y
=
1
1
−
x
2
(\arcsin x)^′=\frac{1}{(\sin y)^′}=\frac{1}{\cos y}=\frac{1}{\sqrt{1-\sin^2y}}=\frac{1}{\sqrt{1-x^2}}
(arcsinx)′=(siny)′1=cosy1=1−sin2y1=1−x21
另外三个同理
2.3、复合函数的求导法则
定理(链式法则):设 u = g ( x ) u=g(x) u=g(x)在 x x x可导, y = f ( u ) y=f(u) y=f(u)在对应 u u u处可导,则 y = f [ g ( x ) ] y=f[g(x)] y=f[g(x)]在 x x x处可导,且 d y d x = d y d u d u d x = f ′ ( u ) g ′ ( x ) \frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}=f^′(u)g^′(x) dxdy=dudydxdu=f′(u)g′(x)
2.4、基本初等函数的导数公式
1
、
(
C
)
′
=
0
1、(C)^′=0
1、(C)′=0
2
、
(
x
a
)
′
=
a
x
a
−
1
2、(x^a)^′=ax^{a-1}
2、(xa)′=axa−1
3
、
(
a
x
)
′
=
a
x
ln
a
3、(a^x)^′=a^x\ln a
3、(ax)′=axlna
4
、
(
e
x
)
′
=
e
x
4、(e^x)^′=e^x
4、(ex)′=ex
5
、
(
log
a
x
)
′
=
1
x
ln
a
5、(\log_ax)^′=\frac{1}{x\ln a}
5、(logax)′=xlna1
6
、
(
ln
∣
x
∣
)
′
=
1
x
6、(\ln |x|)^′=\frac{1}{x}
6、(ln∣x∣)′=x1
7
、
(
sin
x
)
′
=
cos
x
7、(\sin x)^′=\cos x
7、(sinx)′=cosx
8
、
(
cos
x
)
′
=
−
sin
x
8、(\cos x)^′=-\sin x
8、(cosx)′=−sinx
9
、
(
tan
x
)
′
=
sec
2
x
9、(\tan x)^′=\sec^2x
9、(tanx)′=sec2x
10
、
(
cot
x
)
′
=
−
csc
2
x
10、(\cot x)^′=-\csc^2x
10、(cotx)′=−csc2x
11
、
(
sec
x
)
′
=
sec
x
tan
x
11、(\sec x)^′=\sec x\tan x
11、(secx)′=secxtanx
12
、
(
csc
x
)
′
=
−
csc
x
cot
x
12、(\csc x)^′=-\csc x\cot x
12、(cscx)′=−cscxcotx
13
、
(
arcsin
x
)
′
=
1
1
−
x
2
13、(\arcsin x)^′=\frac{1}{\sqrt{1-x^2}}
13、(arcsinx)′=1−x21
14
、
(
arccos
x
)
′
=
−
1
1
−
x
2
14、(\arccos x)^′=-\frac{1}{\sqrt{1-x^2}}
14、(arccosx)′=−1−x21
15
、
(
arctan
x
)
′
=
1
1
+
x
2
15、(\arctan x)^′=\frac{1}{1+x^2}
15、(arctanx)′=1+x21
16
、
(
a
r
c
c
o
t
x
)
′
=
−
1
1
+
x
2
16、(arccot\ x)^′=-\frac{1}{1+x^2}
16、(arccot x)′=−1+x21
3、高阶导数
在前面,我们学习了的都是一阶导数,也就是对一个函数求一次导得到的函数就叫做一阶导数
当我们对一个函数求了一次导数后,会得到一个导函数,如果这个导函数是可导的,我们再对他求导,就会得到二阶导数,以此类推
二阶导数:
(
y
′
)
′
=
y
′
′
=
d
2
y
d
x
2
(y')'=y''=\frac{d^2y}{dx^2}
(y′)′=y′′=dx2d2y
三阶:
y
′
′
′
y'''
y′′′
四阶:
y
(
4
)
y^{(4)}
y(4)
.
.
.
...
...
n阶:
y
(
n
)
=
d
n
y
d
x
n
y^{(n)}=\frac{d^ny}{dx^n}
y(n)=dxndny
若 f ( n ) ( x ) f^{(n)}(x) f(n)(x)在区间 I I I上连续,称 f ( x ) f(x) f(x)在 I I I上n阶连续可导
3.1、高阶导数的公式
设
u
,
v
u,v
u,v都是
n
n
n阶可导,则:
1
、
(
u
±
v
)
(
n
)
=
u
(
n
)
±
v
(
n
)
1、(u±v)^{(n)}=u^{(n)}±v^{(n)}
1、(u±v)(n)=u(n)±v(n)
2
、
L
e
i
b
n
i
z
2、Leibniz
2、Leibniz公式
(
u
v
)
(
n
)
=
∑
k
=
0
n
C
n
k
u
(
n
−
k
)
v
k
(uv)^{(n)}=\sum_{k=0}^nC^k_nu^{(n-k)}v^k
(uv)(n)=∑k=0nCnku(n−k)vk
3
、
(
sin
x
)
(
n
)
=
sin
(
x
+
n
π
2
)
3、(\sin x)^{(n)}=\sin(x+n\frac{π}{2})
3、(sinx)(n)=sin(x+n2π)
4
、
(
cos
x
)
(
n
)
=
cos
(
x
+
n
π
2
)
4、(\cos x)^{(n)}=\cos(x+n\frac{π}{2})
4、(cosx)(n)=cos(x+n2π)
4、隐函数和参数方程确定的函数的导数
4.1、隐函数的导数
显函数:因变量
f
(
x
)
f(x)
f(x)可以通过自变量
x
x
x表示的函数叫做显函数
例如:
y
=
cos
x
,
y
=
x
1
+
x
y = \cos x,y=\frac{x}{1+x}
y=cosx,y=1+xx
隐函数: 因变量
f
(
x
)
f(x)
f(x)不能通过自变量
x
x
x表示出来叫做隐函数
例如:
3
y
+
x
+
1
=
0
3y+x+1=0
3y+x+1=0
上述的隐函数可以显化为显函数 y = − x + 1 3 y=-\frac{x+1}{3} y=−3x+1
但并不是每一个隐函数都可以显化为显函数的
例如:
y
−
x
−
ϵ
sin
y
=
0
(
0
<
ϵ
<
1
)
y-x-ϵ\sin y=0(0<ϵ<1)
y−x−ϵsiny=0(0<ϵ<1)
那么,既然有上述这种很难显化的隐函数,那么我们就要确定一种隐函数的通用求导法则,即:
F
(
x
,
y
)
=
0
,
y
=
f
(
x
)
,
F
(
x
,
f
(
x
)
)
=
0
F(x,y)=0,y=f(x),F(x,f(x))=0
F(x,y)=0,y=f(x),F(x,f(x))=0
此时两边同时对x求导,即可
例如:求由方程
y
5
+
2
y
−
x
=
0
y^5+2y-x=0
y5+2y−x=0确定的隐函数
y
=
f
(
x
)
y=f(x)
y=f(x)的导数
解:
(
y
5
+
2
y
−
x
)
′
=
5
y
4
y
′
+
2
y
′
−
1
(y^5+2y-x)'=5y^4y'+2y'-1
(y5+2y−x)′=5y4y′+2y′−1
y
′
(
5
y
4
+
2
)
=
1
y'(5y^4+2)=1
y′(5y4+2)=1
y
′
=
1
5
y
4
+
2
y'=\frac{1}{5y^4+2}
y′=5y4+21
4.2、由参数方程所确定的函数的导数
定理:设
x
=
φ
(
t
)
,
y
=
ψ
(
t
)
x=φ(t),y=ψ(t)
x=φ(t),y=ψ(t)在
(
α
,
β
)
(α,β)
(α,β)上可导,
φ
′
(
t
)
≠
0
,
φ'(t)≠0,
φ′(t)=0,则
d
y
d
x
=
ψ
′
(
t
)
φ
′
(
t
)
\frac{dy}{dx}=\frac{ψ'(t)}{φ'(t)}
dxdy=φ′(t)ψ′(t)
若
φ
(
t
)
,
ψ
(
t
)
φ(t),ψ(t)
φ(t),ψ(t)二阶可导,则
d
2
y
d
x
2
=
ψ
′
′
(
t
)
φ
′
(
t
)
−
φ
′
′
(
t
)
ψ
′
(
t
)
φ
′
3
(
t
)
\frac{d^2y}{dx^2}=\frac{ψ''(t)φ'(t)-φ''(t)ψ'(t)}{φ'^3(t)}
dx2d2y=φ′3(t)ψ′′(t)φ′(t)−φ′′(t)ψ′(t)
首先根据条件:
φ
′
(
t
)
≠
0
φ'(t)≠0
φ′(t)=0我们可以得到
φ
(
t
)
φ(t)
φ(t)在
(
α
,
β
)
(α,β)
(α,β)上是单调的,那么
x
=
φ
(
t
)
x=φ(t)
x=φ(t)就有反函数
t
=
φ
−
1
(
x
)
t=φ^{-1}(x)
t=φ−1(x)
①
y
=
ψ
(
t
)
,
②
t
=
φ
−
1
(
x
)
①y=ψ(t),②t=φ^{-1}(x)
①y=ψ(t),②t=φ−1(x)
由①②得它的导数为
d
y
d
x
=
d
y
d
t
d
t
d
x
=
ψ
′
(
t
)
φ
′
(
t
)
\frac{dy}{dx}=\frac{dy}{dt}\frac{dt}{dx}=\frac{ψ'(t)}{φ'(t)}
dxdy=dtdydxdt=φ′(t)ψ′(t)
而若
ψ
(
t
)
,
φ
(
t
)
ψ(t),φ(t)
ψ(t),φ(t)二阶可导,则两边再同时对x求一次导得:
d
2
y
d
x
2
=
d
d
t
(
ψ
′
(
t
)
φ
′
(
t
)
)
×
d
t
d
x
\frac{d^2y}{dx^2}=\frac{d}{dt} (\frac{ψ'(t)}{φ'(t)})×\frac{dt}{dx}
dx2d2y=dtd(φ′(t)ψ′(t))×dxdt
=
ψ
′
′
(
t
)
φ
′
(
t
)
−
φ
′
′
(
t
)
ψ
′
(
t
)
φ
′
2
(
t
)
×
1
φ
′
(
t
)
=\frac{ψ''(t)φ'(t)-φ''(t)ψ'(t)}{φ'^2(t)}×\frac{1}{φ'(t)}
=φ′2(t)ψ′′(t)φ′(t)−φ′′(t)ψ′(t)×φ′(t)1
4.3、相关变化率
相变变化率:即 x = x ( t ) , y = y ( t ) x=x(t),y=y(t) x=x(t),y=y(t),并且 x x x和 y y y之间又满足某种关系 F ( x , y ) = 0 F(x,y)=0 F(x,y)=0,那么我们如果知道了 x / y x/y x/y中任意一个变量对t的变化率就可以求出另一个变量与t之间的变化率
例:设有一个倒置的圆锥形容器,其底面圆直径为10cm,高为5cm,现以每秒3cm 3 ^3 3给容器中加水,试求t = 1秒时水面上升的速率
【解】
设水的高度为
h
(
t
)
h(t)
h(t),则水的体积
V
(
t
)
=
π
3
h
2
(
t
)
×
h
(
t
)
V(t)=\frac{π}{3}h^2(t)×h(t)
V(t)=3πh2(t)×h(t)
V
′
(
t
)
=
π
h
2
(
t
)
d
h
d
t
=
3
V'(t)=πh^2(t)\frac{dh}{dt}=3
V′(t)=πh2(t)dtdh=3
由题得:
V
(
1
)
=
3
=
π
3
h
3
(
1
)
,
h
(
1
)
=
3
9
π
V(1)=3=\frac{π}{3}h^3(1),h(1)=^3\sqrt{\frac{9}{π}}
V(1)=3=3πh3(1),h(1)=3π9
那么
V
′
(
1
)
=
3
=
π
(
9
π
)
2
3
d
h
d
t
V'(1)=3=π(\frac{9}{π})^\frac{2}{3}\frac{dh}{dt}
V′(1)=3=π(π9)32dtdh
d
h
d
t
=
3
π
(
9
π
)
−
2
3
\frac{dh}{dt}=\frac{3}{π}(\frac{9}{π})^{-\frac{2}{3}}
dtdh=π3(π9)−32
相关变化率解题方法:
1.先建立两个相关变化率的关系式
F
(
x
,
y
)
F(x,y)
F(x,y)如例题中的体积变化率与高度变化率的关系
2.两边同时对t求导,得到未知相关变化率
5、函数的微分
5.1、引例
当我们得到一个函数时,我们需要计算它从某点
x
0
x_0
x0经过一个变化到达
x
0
+
Δ
x
x_0+Δx
x0+Δx时的函数值的改变量
例如:
f
(
x
)
=
x
2
f(x)=x^2
f(x)=x2
函数改变量:
Δ
y
=
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δy=f(x_0+Δx)-f(x_0)
Δy=f(x0+Δx)−f(x0)
其中
x
0
x_0
x0是定点,
Δ
x
Δx
Δx是动点
Δ
y
=
(
x
0
+
Δ
x
)
2
−
(
x
0
)
2
=
2
x
0
Δ
x
+
(
Δ
x
)
2
Δy=(x_0+Δx)^2-(x_0)^2=2x_0Δx+(Δx)^2
Δy=(x0+Δx)2−(x0)2=2x0Δx+(Δx)2
我们观察上述式子,
(
Δ
x
)
2
(Δx)^2
(Δx)2其实是
Δ
x
Δx
Δx的高阶无穷小,
2
x
0
Δ
x
2x_0Δx
2x0Δx其实才是
Δ
x
Δx
Δx的同阶无穷小
那么
Δ
y
≈
2
x
0
Δ
x
Δy\approx 2x_0Δx
Δy≈2x0Δx
5.2、定义
微分的定义:若 f ( x 0 + Δ x ) − f ( x 0 ) = A Δ x + o ( Δ x ) f(x_0+Δx)-f(x_0)=AΔx+o(Δx) f(x0+Δx)−f(x0)=AΔx+o(Δx)则称 f ( x ) f(x) f(x)在 x 0 x_0 x0点可微, A Δ x AΔx AΔx称为 f ( x ) f(x) f(x)在 x 0 x_0 x0点的微分,记为: d y = A Δ x dy=AΔx dy=AΔx
1.
A
Δ
x
AΔx
AΔx是
Δ
x
Δx
Δx的线性函数
2.
A
Δ
x
AΔx
AΔx是
Δ
x
Δx
Δx的同阶无穷小(主要部分),
o
(
Δ
x
)
o(Δx)
o(Δx)是
Δ
x
Δx
Δx的高阶无穷小
3.
d
y
dy
dy是
Δ
y
Δy
Δy的线性主部
5.3、可微与可导
定理:函数 y = f ( x ) y=f(x) y=f(x)在点 x 0 x_0 x0处可微的充分必要条件是 f ( x ) f(x) f(x)在点 x 0 x_0 x0处可导,且有 d y = f ′ ( x 0 ) Δ x = f ′ ( x ) d x dy=f'(x_0)Δx=f'(x)dx dy=f′(x0)Δx=f′(x)dx
证明:可导 ⇛ \Rrightarrow ⇛可微
f
(
x
0
)
=
lim
Δ
x
→
0
f
(
x
0
+
Δ
x
)
−
f
(
x
)
Δ
x
=
f
′
(
x
0
)
+
α
(
x
)
f(x_0)=\lim_{Δx \to 0}\frac{f(x_0+Δx)-f(x)}{Δx}=f'(x_0)+α(x)
f(x0)=limΔx→0Δxf(x0+Δx)−f(x)=f′(x0)+α(x)
lim
Δ
x
→
0
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
=
f
′
(
x
0
)
Δ
x
+
α
(
x
)
Δ
x
=
f
′
(
x
0
)
Δ
x
+
o
(
Δ
x
)
\lim_{Δx \to 0}f(x_0+Δx)-f(x_0)=f'(x_0)Δx+α(x)Δx=f'(x_0)Δx+o(Δx)
limΔx→0f(x0+Δx)−f(x0)=f′(x0)Δx+α(x)Δx=f′(x0)Δx+o(Δx)
证明:可导 ⇚ \Lleftarrow ⇚可微
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
=
A
Δ
x
+
o
(
Δ
x
)
f(x_0+Δx)-f(x_0)=AΔx+o(Δx)
f(x0+Δx)−f(x0)=AΔx+o(Δx)
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
=
A
+
o
(
Δ
x
)
Δ
x
\frac{f(x_0+Δx)-f(x_0)}{Δx}=A+\frac{o(Δx)}{Δx}
Δxf(x0+Δx)−f(x0)=A+Δxo(Δx)
5.4、微分的几何意义

导数的几何意义在一点处的导数就是这一点切线的斜率,就是图中的
tan
α
\tan α
tanα
tan
α
=
d
y
Δ
x
,
d
y
=
t
a
n
α
Δ
x
=
f
′
(
x
)
Δ
x
\tan α=\frac{dy}{Δx},dy=tanαΔx=f'(x)Δx
tanα=Δxdy,dy=tanαΔx=f′(x)Δx
微分
d
y
=
f
′
(
x
)
d
x
dy=f'(x)dx
dy=f′(x)dx在几何上表示曲线
y
=
f
(
x
)
y=f(x)
y=f(x)的切线上的增量
用通俗的语言来说,函数在这一点处的微分 d y dy dy表示的是在这一点的切线上两个函数值之间的差,而 Δ y Δy Δy表示的是在这一曲线上两个函数值之间的差, Δ y Δy Δy是精确值,而 d y dy dy是近似值,微分的思想就是把曲线用值线表示,把非均匀变化用均匀变化表示
5.5、微分的运算法则
设
u
u
u和
v
v
v都可微,则:
1、
d
(
u
±
v
)
=
d
u
±
d
v
d(u \pm v)=du\pm dv
d(u±v)=du±dv
2、
d
(
u
v
)
=
v
d
u
+
u
d
v
d(uv)=vdu+udv
d(uv)=vdu+udv
3、
d
(
u
v
)
=
v
d
u
−
u
d
v
v
2
(
v
≠
0
)
d(\frac{u}{v})=\frac{vdu-udv}{v^2}(v ≠0)
d(vu)=v2vdu−udv(v=0)
复合函数微分法则
设
y
=
f
(
u
)
y=f(u)
y=f(u)可微,
u
=
g
(
x
)
u=g(x)
u=g(x)可微,则
y
=
f
(
g
(
x
)
)
y=f(g(x))
y=f(g(x))可微,且
d
y
=
y
x
′
d
x
=
y
u
′
u
x
′
d
x
=
y
u
′
d
u
dy=y'_xdx=y'_uu'_xdx=y'_udu
dy=yx′dx=yu′ux′dx=yu′du
d
y
=
dy=
dy=中间变量导数✖中间变量微分=自变量导数✖自变量微分
我们把这个性质就叫做微分形式不变性