目录
一、堆
二、Java里的集合类PriorityQueue
1、优先级队列的概念
2、构造方法
3、常用方法
1.入队offer
2.出队poll
3.获取队首元素peek
4.扩容机制
4、 注意事项
三、实现大根堆
1、准备字段
2、创建大根堆
3、offer
4、poll
5、peek
一、堆
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<=K2i+2 ,则称为小堆(或大堆)。堆底层是完全二叉树,因为是完全二叉树所以存储时可选择数组进行存储
二、Java里的集合类PriorityQueue
1、优先级队列的概念
在出队的时候返回的是优先级最高的元素,这种队列叫做优先级队列
2、构造方法
| 构造方法 | 说明 |
| PriorityQueue() | 无参构造,此时默认长度为11 |
| PriorityQueue(int initialCapacity) | 传入队列的长度 |
| PriorityQueue(Comparator<? super E> comparator) | 传入比较器,用于后续优先级比较 |
| PriorityQueue(nt initialCapacity,Comparator<? super E> comparator) | 同时传入长度与比较器 |
PriorityQueue(Collection<? extends E> c) | 通过其他集合类构造优先级队列 |
3、常用方法
1.入队offer
如果传入的对象为空就抛出异常。第一次插入直接放在下标为0的地方,如果后续存入,就调用向上调整进而维护为堆,向上调整在下面实现堆中会讲到
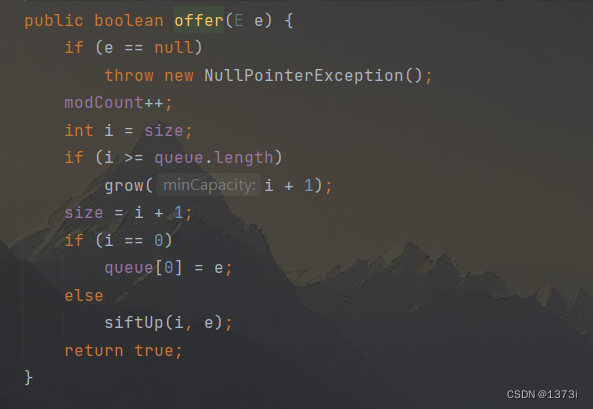
2.出队poll
出队操作本质是将队首也就是下标为0的元素与队尾元素进行交换,然后让有效数据个数size--,再调用向上调整维护堆结构
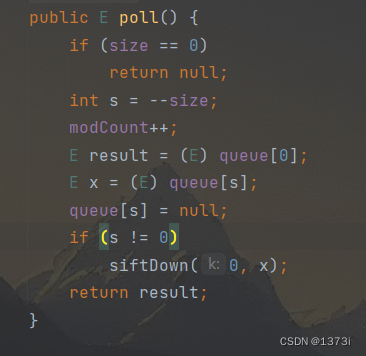
3.获取队首元素peek
获取下标为0的元素

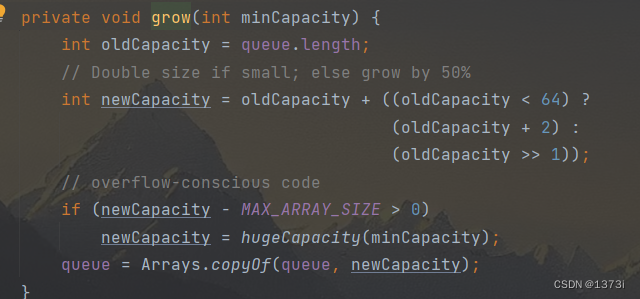
4.扩容机制
如果在堆满的情况下入队,就会调用grow进行扩容,而原码实现扩容时,如果现在容量小于64则采取2倍扩容,超出后则1.5倍扩容
4、 注意事项
使用PriorityQueue时传入的类型要实现Comparable接口或者在构造方法时手动传入比较器,且传入空会异常,如果在多线程情况下推荐使用PriorityBlockingQueue
三、实现大根堆
1、准备字段
public class MyHeap <T extends Comparable<T>{
private Object[] queue; //底层数组
private int size; //有效数据个数
private static final int DEFAULT_SIZE = 11;
/**
* 构造方法默认长度为11
*/
public MyHeap(){
this.queue = new Object[DEFAULT_SIZE];
}
/**
* 构造方法初始数组长度
* @param initialCapacity 容量
*/
public MyHeap(int initialCapacity){
this.queue = new Object[initialCapacity];
}
}2、创建大根堆
在使用构造方法传入一个数组时,这个数组不是堆,我们调用heapIfy方法将其先创建成一个大根堆
/**
* 传入数组
* @param e
*/
public MyHeap(Object[] e){
this.queue = e;
this.size = e.length;
heapIfy();
}
/**
* 创建大根堆
*/
private void heapIfy(){
for(int parent = (size - 1 - 1) / 2; parent >= 0; parent--){
siftDown(parent,this.size);
}
}比如一组数据 1 2 3 4 5 6,我们将他创建成一个大根堆时,我们先从最后一个位置所在的树开始进行调整,由于我们能获取到数组的长度,且根据堆的性质父亲节点的下标 * 2 + 1就孩子节点下标可知,知道孩子的下标(数组长度-1)就能知道父亲的下标。拿到3后与孩子里的最大值进行比较,如果孩子大就交换
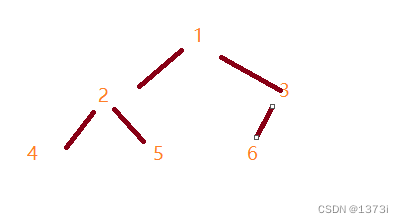
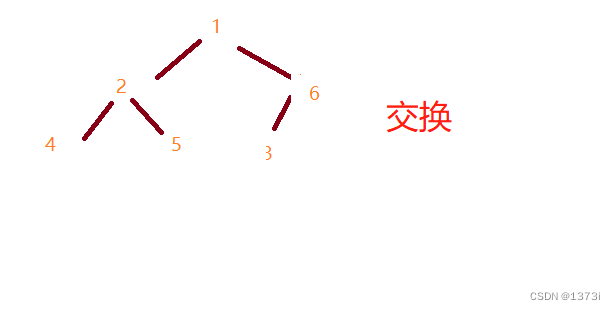
交换之后,如果孩子下面还有数据
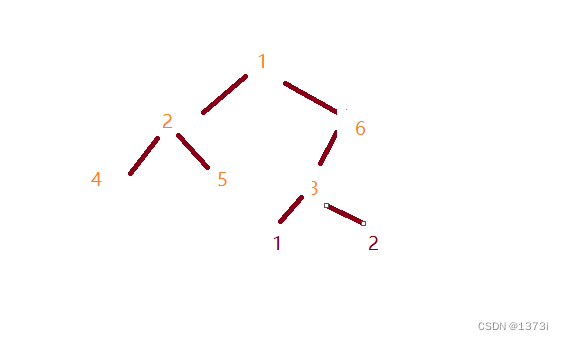
此时即需要继续进行调整,此时让原来的父亲变为原来的孩子,让原来的孩子变为现在父亲的孩子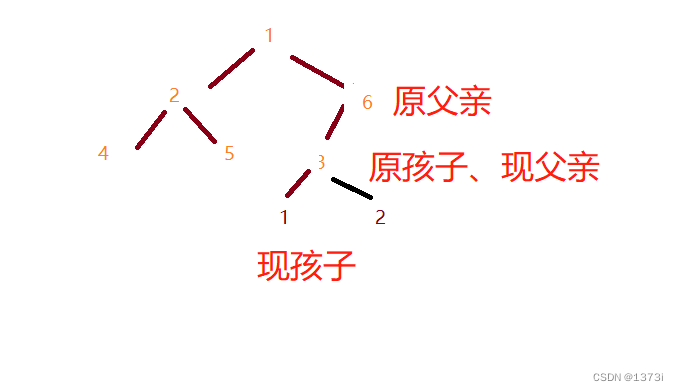
继续重复上述的操作,比较交换,直到孩子的下标不存在时或者不再需要交换时即可
/**
* 传入数组
* @param e
*/
public MyHeap(Object[] e){
this.queue = e;
this.size = e.length;
heapIfy();
}
/**
* 创建大根堆
*/
private void heapIfy(){
for(int parent = (size - 1 - 1) / 2; parent >= 0; parent--){
siftDown(parent,this.size);
}
}
/**
* 向下调整
* @param parent
* @param size
*/
private void siftDown(int parent, int size) {
int child = parent * 2 + 1;
while(child < size){
//先找到两个孩子的最大值,要保证有右孩子也就是child+1得存在
if(child + 1 < size && ((T)queue[child]).compareTo((T)queue[child + 1]) <= 0){
//此时右孩子大,下标右移
child++;
}
//再将最大值与父亲比较
if(((T)queue[child]).compareTo((T)queue[parent]) <= 0){
//此时父亲节点大直接结束循环
break;
}else{
//交换两个值
T tmp = (T)queue[child];
queue[child] = (T)queue[parent];
queue[parent] = tmp;
//再向下走
parent = child;
child = 2 * parent + 1;
}
}
}3、offer
我们在实现入队时,先让数据存入数组的最后一个位置,然后再进行向上调整将数据维护成大根堆
比如我们在大根堆 4 3 2 2 1 1的堆里插入11,先将11存在最后,然后拿他与父亲比较,如果大就交换,如果不比父亲大那他就是大根堆不需要调整,此时交换后,要继续更换父亲与儿子的位置重复比较交换操作,直到孩子下标小于或者等于0时不在需要调整
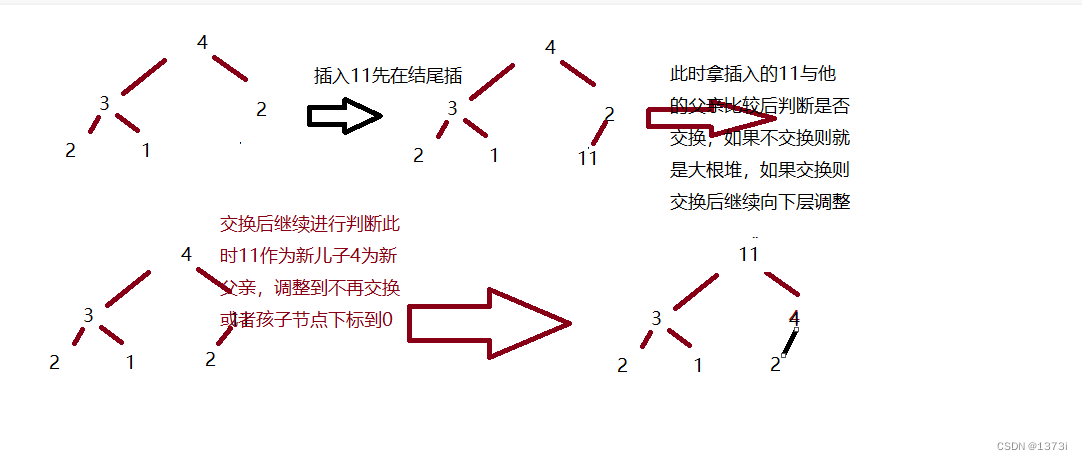
/**
* offer
* @param data
*/
public void offer(T data){
//1.如果满了就扩容
if(size == queue.length){
grow();
}
//2.存入数组末尾
queue[size++] = data;
//3.进行向上调整
siftUp(size - 1);
}
/**
* 扩容
*/
private void grow() {
queue = Arrays.copyOf(queue,queue.length * 2);
}
/**
* 向上调整
* @param child
*/
private void siftUp(int child) {
int parent = (child - 1) / 2;
while(child > 0){
//找到父亲的下标,与父亲进行比较
if(((T)queue[child]).compareTo((T)queue[parent]) <= 0){
//父亲的值大直接结束
break;
}else{
//进行交换
T tmp = (T)queue[child];
queue[child] = (T)queue[parent];
queue[parent] = tmp;
//跟新父亲与儿子的位置
child = parent;
parent = (child - 1) / 2;
}
}
}4、poll
出队操作是将队首元素返回并删除,我们实现时,先记录他的值,然后在将他与最后一个元素交换位置,将有效数据个数-1(删除),此时只有0下标需要调整,然后此时再将数组进行向下调整即可维护大根堆
/**
* poll
* @return
*/
public T poll(){
//1.如果空就返回null
if(isEmpty()){
return null;
}
//2.记录值然后交换删除
T tmp = (T)queue[0];
queue[0] = (T)queue[size - 1];
queue[size - 1] = tmp;
size--; //delete
//3.最后调整
siftDown(0,size);
//4.返回队首元素
return tmp;
}
/**
* 判空
* @return
*/
private boolean isEmpty() {
return size == 0;
}5、peek
获取队首元素,也就是0下标的元素
/**
* peek
* @return
*/
public T peek(){
//1.判空
if(isEmpty()){
return null;
}
//2.返回
return (T)queue[0];
}.


![[机缘参悟-95] :不同人生、社会问题的本质](https://img-blog.csdnimg.cn/img_convert/85631530ea018ce54650f42cdc126b41.jpeg)