题目地址leetcode10
本题的解题思路
题目中的匹配是一个逐步匹配的过程,我们每次从字符串p中取一个字符出来,有两种可能,一种是取出来字母字符或者‘.’,另外一种是取出来[字符+‘*’]组合,他可以在s中匹配任意自然数个字符,并不具备唯一性,因此我们可以考虑使用动态规划,对匹配的方案进行枚举。
- 如果 p p p 的第 j j j 个字母是小写字母,那么我们必须在 s s s 中匹配一个相同的小写字母
我们用 f [ i ] [ j ] f[i][j] f[i][j] 表示 s s s 的前 i i i 个字符与 p p p 中的前 j j j 个字符是否可以匹配,那么就有状态转移方程
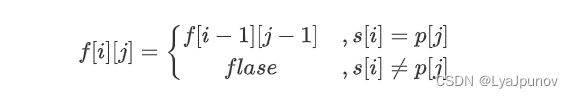
- 如果 p p p 的第 j j j 个字母是 ∗ * ∗,那么我们可以匹配多次
匹配零次的话有(也就是我们没有匹配任何字符)
f
[
i
]
[
j
]
=
f
[
i
]
[
j
−
2
]
f[i][j] = f[i][j-2]
f[i][j]=f[i][j−2]
匹配一次
f
[
i
]
[
j
]
=
f
[
i
−
1
]
[
j
−
2
]
,
i
f
s
[
i
]
=
p
[
j
−
1
]
f[i][j] = f[i-1][j-2],if \; s[i]=p[j-1]
f[i][j]=f[i−1][j−2],ifs[i]=p[j−1]
匹配两次
f
[
i
]
[
j
]
=
f
[
i
−
2
]
[
j
−
2
]
,
i
f
s
[
i
−
1
]
=
s
[
i
]
=
p
[
j
−
1
]
f[i][j] = f[i-2][j-2],if \; s[i-1]=s[i]=p[j-1]
f[i][j]=f[i−2][j−2],ifs[i−1]=s[i]=p[j−1]
匹配三次
f
[
i
]
[
j
]
=
f
[
i
−
3
]
[
j
−
2
]
,
i
f
s
[
i
−
2
]
=
s
[
i
−
1
]
=
s
[
i
]
=
p
[
j
−
1
]
f[i][j] = f[i-3][j-2],if \; s[i-2]=s[i-1]=s[i]=p[j-1]
f[i][j]=f[i−3][j−2],ifs[i−2]=s[i−1]=s[i]=p[j−1]
这里我个人理解起来是有点困难的,为什么匹配一次的话,状态转移就是
i
i
i向前移一位呢,不应该是向后匹配嘛,其实这里是因为我的思维和深度优先搜索有点混淆了,这里我们只考虑状态转移,只考虑马尔科夫决策过程,这样想的话就是想的通了。
但是这样依旧麻烦,因为我需要枚举到底要匹配多少字符,导致时间复杂度升高,其实本质上只有两种情况
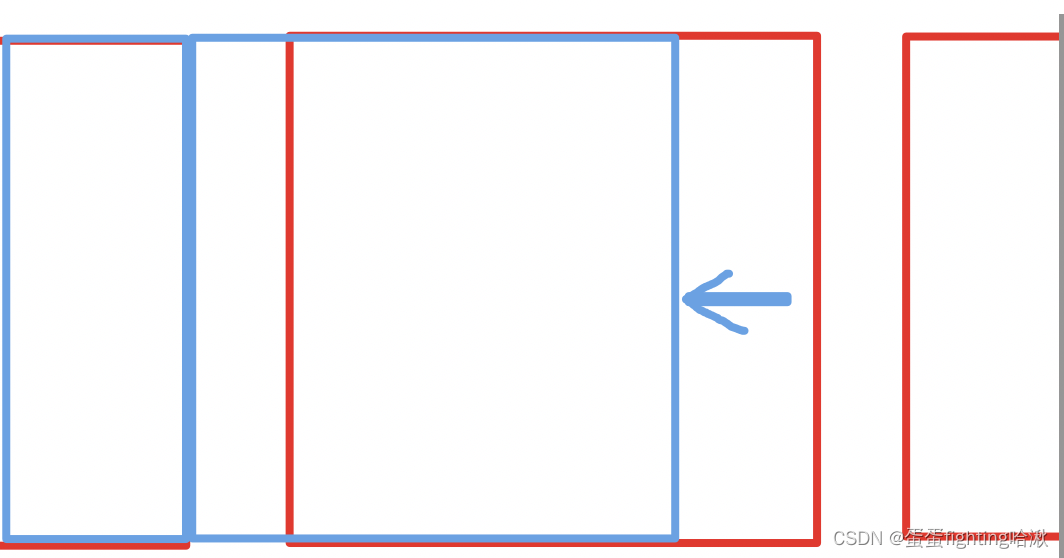
(1) 匹配 s s s 末尾的一个字符,将该字符扔掉,而该组合还可以继续进行匹配;
(2) 不匹配字符,将该组合扔掉,不再进行匹配。
所以写出状态转移方程
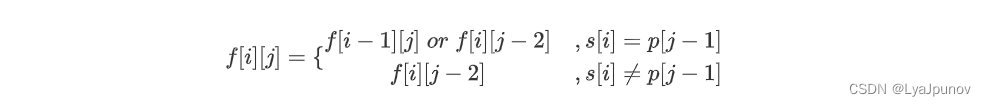
这里是很巧妙的,如果s的前 i − 1 i-1 i−1位字符和p的前 j j j位字符可以匹配的话,那么这一位可以匹配就可以
如果s的前 i i i位字符和p的前 j − 2 j-2 j−2位字符可以匹配的话,那么这一位也可以匹配
- 在任意情况下,只要 p [ j ] p[j] p[j]是‘.’,那么 p [ j ] p[j] p[j]是一定成功匹配 s s s中的任意一个小写字母,最终状态转移方程为
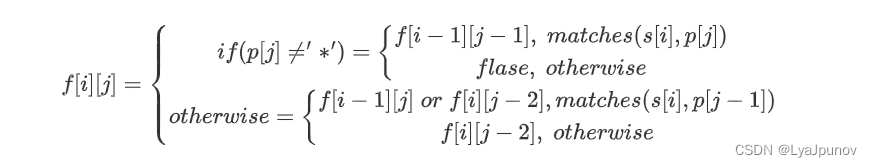
其中matches(x,y) 判断两个字符是否匹配的辅助函数。只有当y是’.',或者x和y本身相同时,这两个字符才会匹配。
动态规划的边界条件为 f [ 0 ] [ 0 ] = t r u e f[0][0]=true f[0][0]=true,即两个空字符串是可以匹配的。最终的答案即为 f [ m ] [ n ] f[m][n] f[m][n],其中 m m m和 n n n分别是字符串s和p的长度。由于大部分语言中,字符串的字符下标是从0开始的,因此在实现上面的状态转移方程时,需要注意每一维下标与实际字符下标的对应关系。
在上面的状态转移方程中,如果字符串p中包含一个「字符 + 星号」的组合,那么在进行状态转移时,会先将a进行匹配,再将a*作为整体进行匹配,这样做看起来像是将a多进行了一次状态转移,实际上是这样吗?答案是:不是。为什么呢,因为无论a匹配的对或错,这一次的状态转移结果在后面的运算中都没有用到。
整体代码
class Solution {
public:
bool isMatch(string s, string p) {
int m = s.size();
int n = p.size();
// 这里的matches函数像是lambda表达式,他是一个函数,执行下面的程序
// ()小括号中是形参列表;{}括号中是函数体,因为是定义函数,大括号后面记得加 ; 分号。
auto matches = [&](int i, int j) {
if (i == 0) {
return false;
}
if (p[j - 1] == '.') {
return true;
}
return s[i - 1] == p[j - 1];
};
vector<vector<int>> f(m + 1, vector<int>(n + 1));
f[0][0] = true;
for (int i = 0; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (p[j - 1] == '*') {
f[i][j] |= f[i][j - 2];
if (matches(i, j - 1)) {
f[i][j] |= f[i - 1][j];
}
}
else {
if (matches(i, j)) {
f[i][j] |= f[i - 1][j - 1];
}
}
}
}
return f[m][n];
}
};
总结:动态规划的精髓状态转移,这个题也是这样的,下一个状态只与上一个状态有关
ps:数学公式的支持有点差