深度学习 | Pytorch深度学习实践（Chapter 1~9）

一、overview

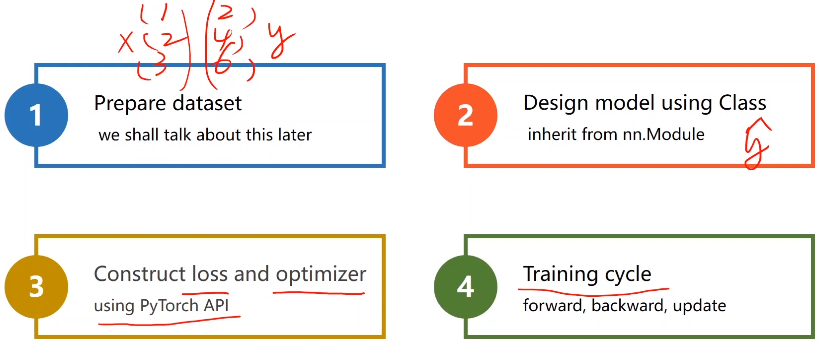
基于pytorch的深度学习的四个步骤基本如下：

二、线性模型 - Linear Model

基本概念

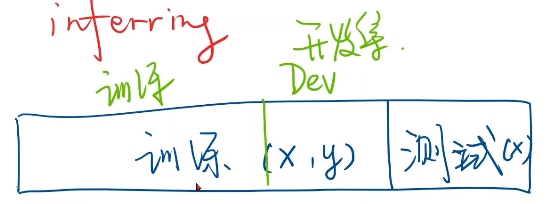
数据集分为测试集和训练集（训练集、开发集）
训练集（x，y）测试集只给（x）
过拟合：模型学得太多导致性能不好
开发集：测验模型泛化能力
zip：从数据集中，按数据对儿取出自变量x_val和真实值y_val

本例中进行人工training，穷举法
定义前向传播函数forward
定义损失函数loss
MSE：平均平方误差
zip：从数据集中，按数据对儿取出自变量x_val和真实值y_val

import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

def forward(x):#定义模型
    return x * w

def loss(x,y):#定义损失函数
    y_pred = forward(x)
    return (y_pred - y) * (y_pred - y)

w_list=[]#权重
mse_list=[]
for w in np.arange(0.0,4.1,0.1):
    print('w=',w)
    l_sum = 0
    for x_val,y_val in zip(x_data,y_data):
        y_pred_val = forward(x_val)
        loss_val = loss(x_val,y_val)
        l_sum += loss_val
        print('\t',x_val,y_val,y_pred_val,loss_val)
    print('MSE=',l_sum / 3)
    w_list.append(w)
    mse_list.append(l_sum / 3)

plt.plot(w_list,mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()

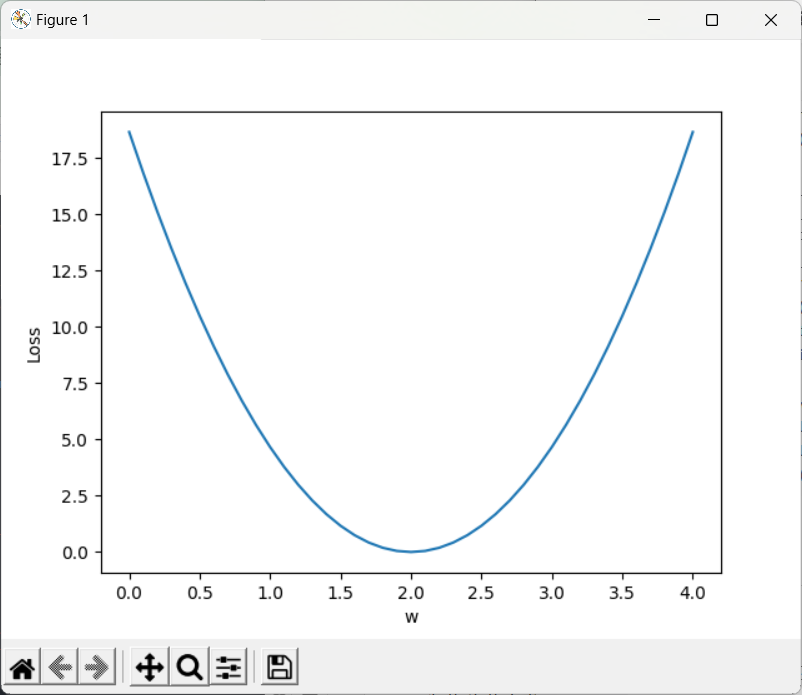
注：模型训练可视化

wisdom：可视化工具包

三、梯度下降 - Gradient Descent

3.1、梯度下降

（基于cost function 即所有样本）：

如我们想要找到w的最优值

贪心思想：每一次迭代得到局部最优，往梯度的负方向走
梯度下降算法很难找到全局最优，但是在深度学习中损失函数中，全局最优最有很少出现，但会出现鞍点（梯度 = 0）

import numpy as np
import matplotlib.pyplot as plt

w = 1.0
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

def forward(x):
    return x * w

def cost(xs,ys):
    cost = 0
    for x,y in zip(xs,ys):
        y_pred = forward(x)
        cost += (y_pred-y)**2
    return cost / len(xs)

def gradient(xs,ys):
    grad = 0
    for x,y in zip(xs,ys):
        grad += 2 * x * ( x * w - y)
    return grad / len(xs)

epoch_list=[]
cost_list=[]
print('Predict (before training)',4,forward(4))
for epoch in range(100):
    cost_val = cost(x_data,y_data)
    grad_val = gradient(x_data,y_data)
    w -= 0.01 * grad_val
    print('Epoch',epoch,'w=',w,'loss=',cost_val)
    epoch_list.append(epoch)
    cost_list.append(cost_val)
print('Predict (after training)',4,forward(4))

print('Predict (after training)',4,forward(4))
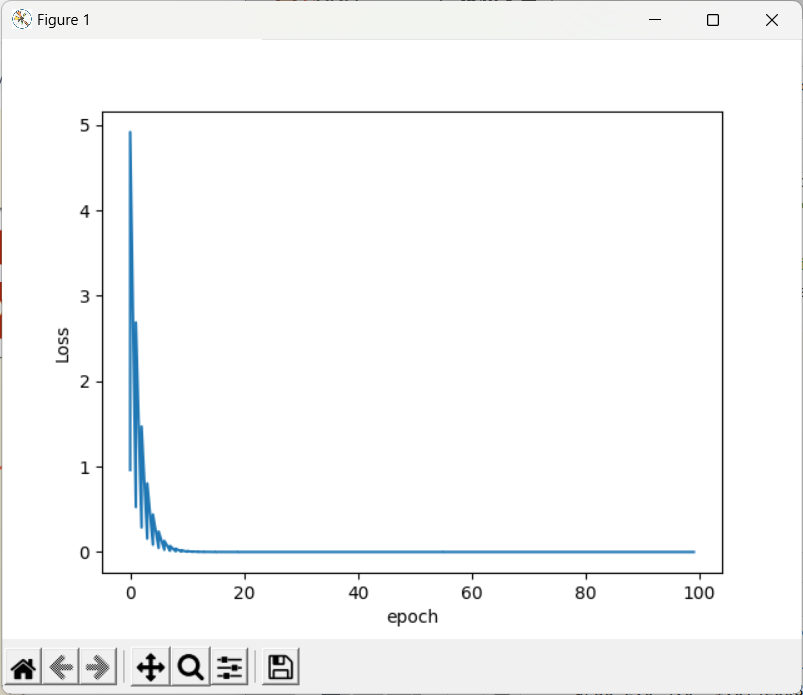
plt.plot(epoch_list,cost_list)
plt.ylabel('Loss')
plt.xlabel('epoch')
plt.show()

注：训练过程会趋近收敛
若生成图像局部震荡很大，可以进行指数平滑
若图像发散，则训练失败，通常原因是因为学习率过大

3.2、随机梯度下降 Stochastic Gradient Descent

（基于单个样本的损失函数）：

—— 因为函数可能存在鞍点，使用一个样本就引入了随机性

此时梯度更新公式为：

与之前的区别：

cost改为loss
梯度求和变为单个样本
训练过程中要对每一个样本求梯度进行更新
由于两个样本的梯度下降不能并行化，时间复杂度太高
所以折中的方式：使用 Mini-Batch 批量随机梯度下降
若干个一组，后续将会涉及

import numpy as np
import matplotlib.pyplot as plt

w = 1.0
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

def forward(x):
    return x * w

def loss(x,y):
    y_pred = forward(x)
    return (y_pred-y)**2

def gradient(x,y):
    return 2 * x * (x * w - y)

loss_list=[]
epoch_list=[]
print('Predict (before training)',4,forward(4))

for epoch in range(100):
    for x,y in zip(x_data,y_data):
        grad = gradient(x,y)
        w = w - 0.01 * grad
        print('\tgrad',x,y,grad)
        l = loss(x,y)
        loss_list.append(l)
        epoch_list.append(epoch)
    print("progress",epoch,'w=',w,'loss=',l)

print('Predict (after training)',4,forward(4))
plt.plot(epoch_list,loss_list)
plt.ylabel('Loss')
plt.xlabel('epoch')
plt.show()

四、反向传播 - BackPropagation

对于复杂的网络：

举例来讲两层神经网络

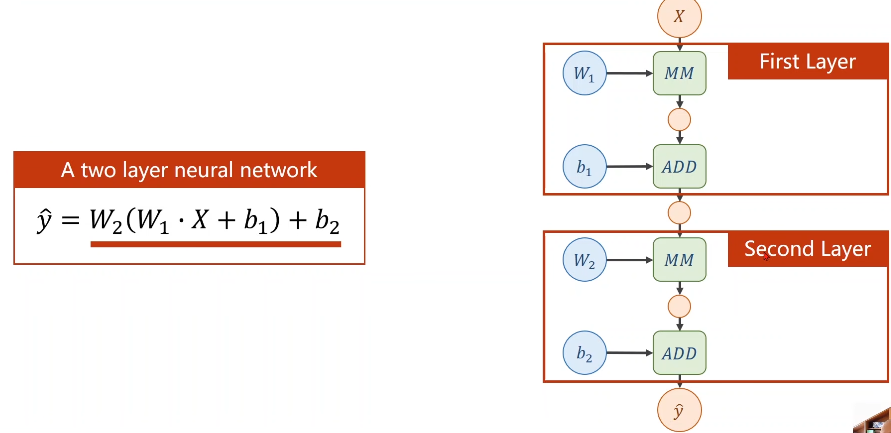
若进行线性变换，不管多少层，最终都可以统一成一种形式，但为了让你不能在化简（即提高模型复杂程度），所以我们要对每一层最终的输出

加一个非线性的变化函数（比如sigmiod）

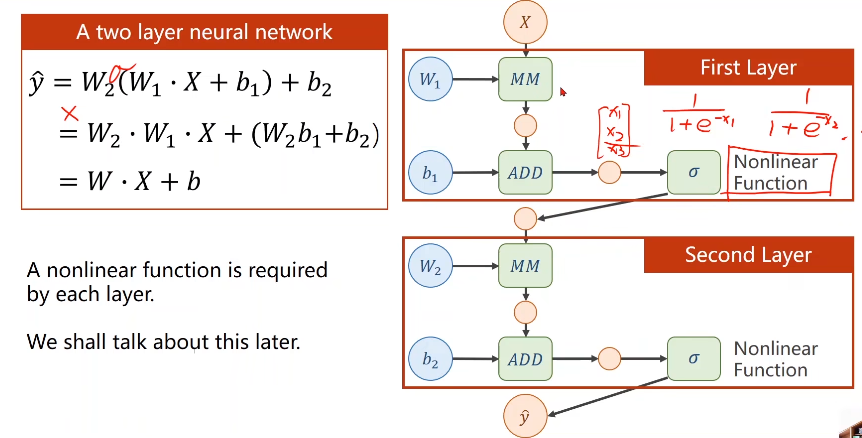
则层层叠加若需要求梯度的话就要用到 —— 链式求导：

1、构建计算图 —— 前馈计算（Forward）先计算最终的loss

2、反馈（Backward）

来看一下最简单的线性模型中的计算图的计算过程：

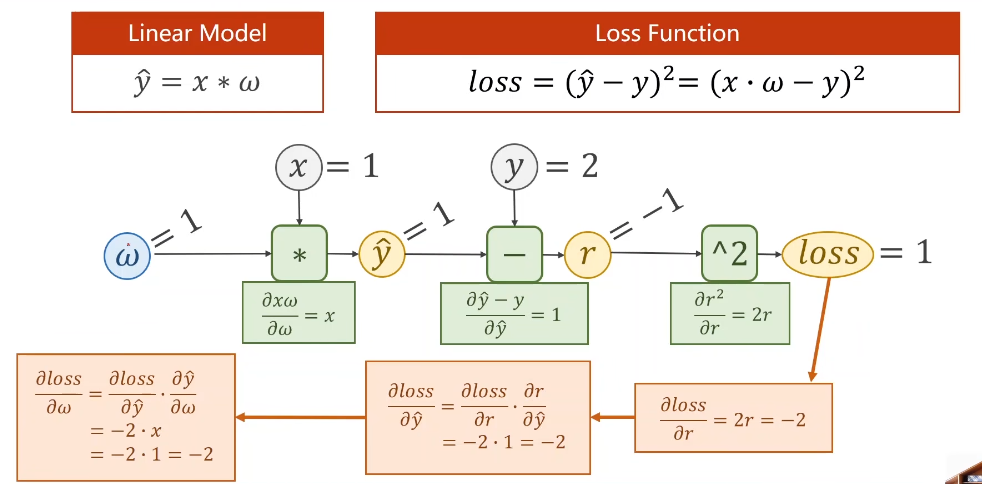
在pytorch中，使用tensor类型的数据

import torch
import matplotlib.pyplot as plt

x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

w = torch.Tensor([1.0]) #注意这里一定要加[] 权重初始值
w.requires_grad = True

def forward(x):
    return x * w #因为w是Tensor，这里的运算符已经被重载了，x会进行自动转换，即构造了计算图

def loss(x,y):
    y_pred = forward(x)
    return (y_pred - y) ** 2

epoch_list = []
loss_list = []
print('Predict (before training)',4,forward(4))

for epoch in range(100):
    #sum=0
    for x,y in zip(x_data,y_data):
        l = loss(x,y) #只要一做backward计算图会释放，会准备下一次的图
        l.backward()
        print('\tgrad:',x,y,w.grad.item()) #item将梯度数值直接拿出来为标量
        w.data = w.data - 0.01 * w.grad.data #grad必须要取到data

        #sum += l 但l为张量，计算图，进行加法计算会构造计算图，将会发生溢出

        w.grad.data.zero_() #！！！权重里面梯度的数据必须显式清零

        print("progress",epoch,l.item())
        epoch_list.append(epoch)
        loss_list.append(l.item())

print('Predict (after training)',4,forward(4))
plt.plot(epoch_list,loss_list)
plt.ylabel('Loss')
plt.xlabel('epoch')
plt.show()

五、利用PyTorch实现线性回归模型 - Linear Regression With PyTorch

pytorch神经网络四步走

1、构建数据集
2、设计模型（用来计算y_hat）
3、构建损失函数和优化器（我们使用pytorch封装的API）
4、训练周期（前馈反馈更新）

本例将使用 Mini-Batch，numpy有广播机制矩阵相加会自动扩充。

使用pytorch的关键就不在于求梯度了，而是构建计算图，这里使用仿射模型，也叫线性单元。

代码实现：

import torch
import matplotlib.pyplot as plt

# 1、准备数据
x_data = torch.Tensor([[1.0],[2.0],[3.0]])
y_data = torch.Tensor([[2.0],[4.0],[6.0]])

# 2、构建模型
class LinearModel(torch.nn.Module):
    def __init__(self): #构造函数
        super(LinearModel,self).__init__()
        self.linear = torch.nn.Linear(1,1) #构造一个对象

    def forward(self,x):
        y_pred = self.linear(x) #实现可调用对象
        return y_pred

model = LinearModel()

# 3、构造损失函数和优化器
criterion = torch.nn.MSELoss(size_average=False) #继承nn.Module，是否求平均
optimizer = torch.optim.SGD(model.parameters(),lr=0.01) #是一个类，不继承nn.Module，不会构建计算图，lr学习率

epoch_list = []
loss_list = []

for epoch in range(100):
    # 前馈 计算 y_hat
    y_pred = model(x_data)
    # 前馈 计算损失
    loss = criterion(y_pred,y_data) #loss标量
    print(epoch,loss) # loss是一个对象，打印将会自动调用__str__()

    optimizer.zero_grad() # 所有权重梯度归零
    # 反馈 反向传播
    loss.backward()
    # 自动更新，权重进行更新
    optimizer.step()

    epoch_list.append(epoch)
    loss_list.append(loss.item())

# Output weight and bias
print('w = ',model.linear.weight.item())
print('b = ',model.linear.bias.item())

# Test Model
x_test = torch.Tensor([4.0])
y_test = model(x_test)
print('y_pred = ',y_test.data)
plt.plot(epoch_list,loss_list)

plt.ylabel('Loss')
plt.xlabel('epoch')
plt.show()

六、逻辑斯蒂回归 - Logistics Regression 逻辑斯蒂回归

—— 虽然叫回归模型，但既可解决分类模型，也可解决回归模型
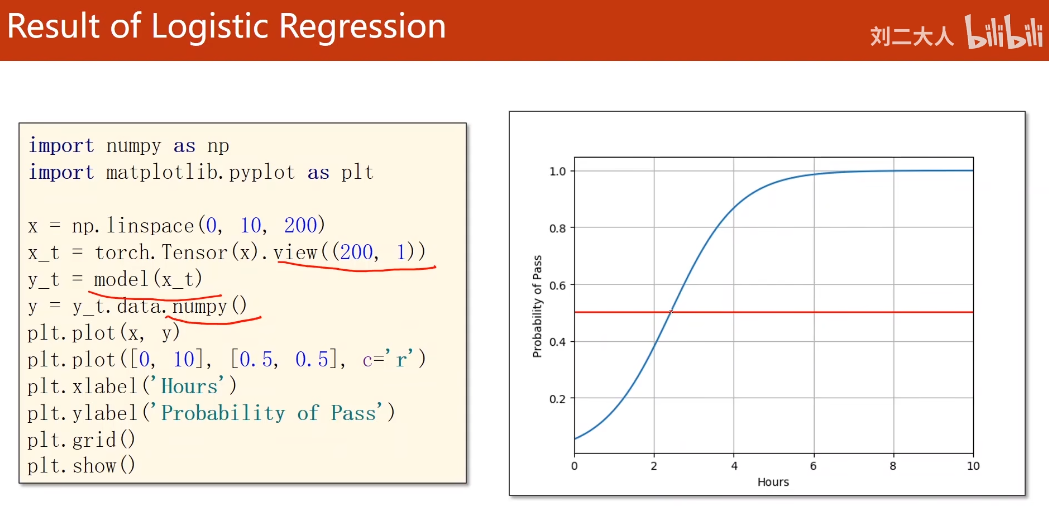
本节是讲的二分类，背景是：学习多少小时能够考试通过；
训练好模型以后，直接用来预测，4小时的学习，能够通过的概率是多大？

torchvision提供相应的数据集，可以指定需要的数据集，train表示需要训练集还是测试集。
分类问题我们的输出为概率，将线性模型输出的实数空间映射到[0,1]之间，logist函数即可完成这个映射。
logist函数为饱和函数，是sigmoid中最典型的。

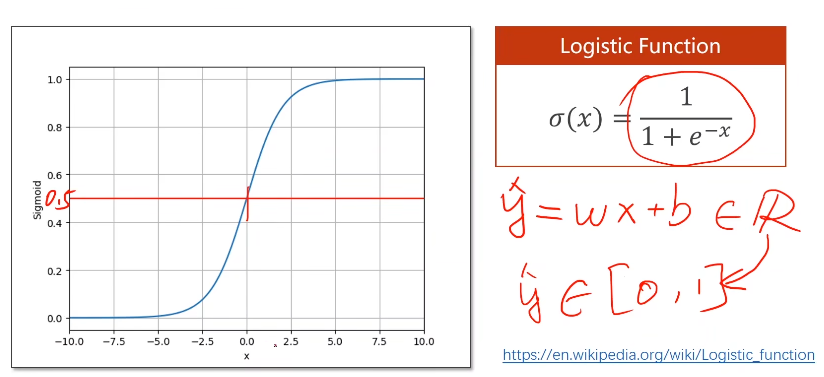
其他的sigmoid函数：

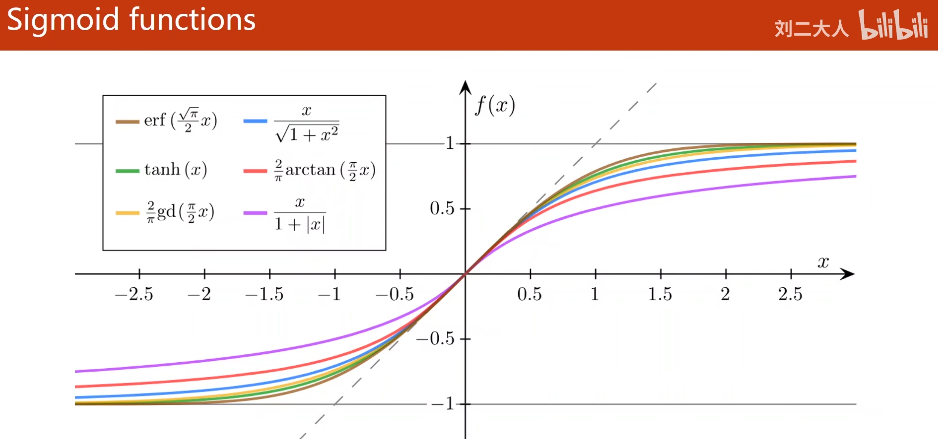
所以现在我们的模型：

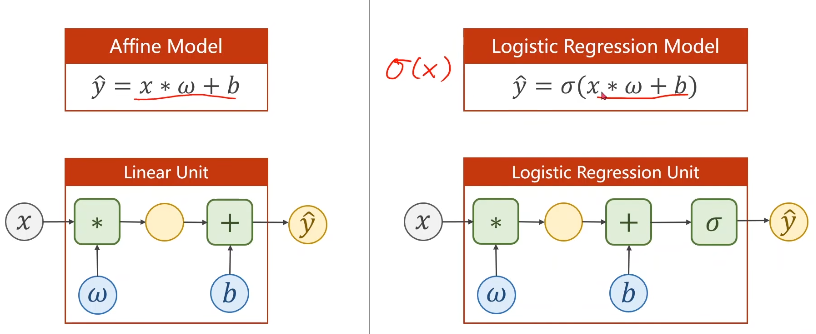
对应的loss也要发生改变，现在输出的是一个分布，不再是一个数值，

所以现在相比较的是两个分布之间的差异：可以选择用KL散度或者cross-entropy(交叉熵)

交叉熵举例：交叉熵越大越好

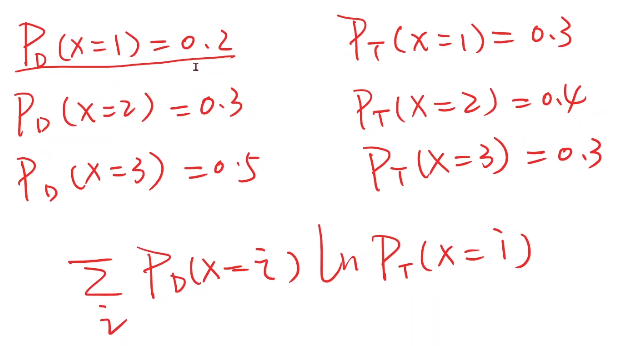
在本例中我们采用二分类的交叉熵，因为加了负号，所以这里的loss越小越好，称为BCE损失

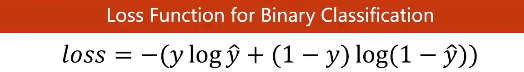
criterion = torch.nn.BCELoss(size_average=False) #继承nn.Module，是否给每个批量求均值，设置与否关键会影响学习率的设置，因为如果损失变小了，将来求出来的导数也会乘上这个常数

import torchvision
import torch.nn.functional as F
import torch
import matplotlib.pyplot as plt

# 1、准备数据
x_data = torch.Tensor([[1.0],[2.0],[3.0]])
y_data = torch.Tensor([[0],[0],[1]])

# 2、构建模型
class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegressionModel,self).__init__()
        self.linear = torch.nn.Linear(1,1)

    def forward(self,x):
        y_pred = F.sigmoid(self.linear(x))
        return y_pred

model = LogisticRegressionModel()

# 3、构造损失函数和优化器
criterion = torch.nn.BCELoss(size_average=False) #继承nn.Module，是否给每个批量求均值
optimizer = torch.optim.SGD(model.parameters(),lr=0.01) #是一个类，不继承nn.Module，不会构建计算图，lr学习率

epoch_list = []
loss_list = []

for epoch in range(1000):
    # 前馈 计算 y_hat
    y_pred = model(x_data)
    # 前馈 计算损失
    loss = criterion(y_pred,y_data) #loss标量
    print(epoch,loss) # loss是一个对象，打印将会自动调用__str__()

    optimizer.zero_grad() # 所有权重梯度归零
    # 反馈 反向传播
    loss.backward()
    # 自动更新，权重进行更新
    optimizer.step()

    epoch_list.append(epoch)
    loss_list.append(loss.item())

# Output weight and bias
print('w = ',model.linear.weight.item())
print('b = ',model.linear.bias.item())

# Test Model
x_test = torch.Tensor([4.0])
y_test = model(x_test)
print('y_pred = ',y_test.data)
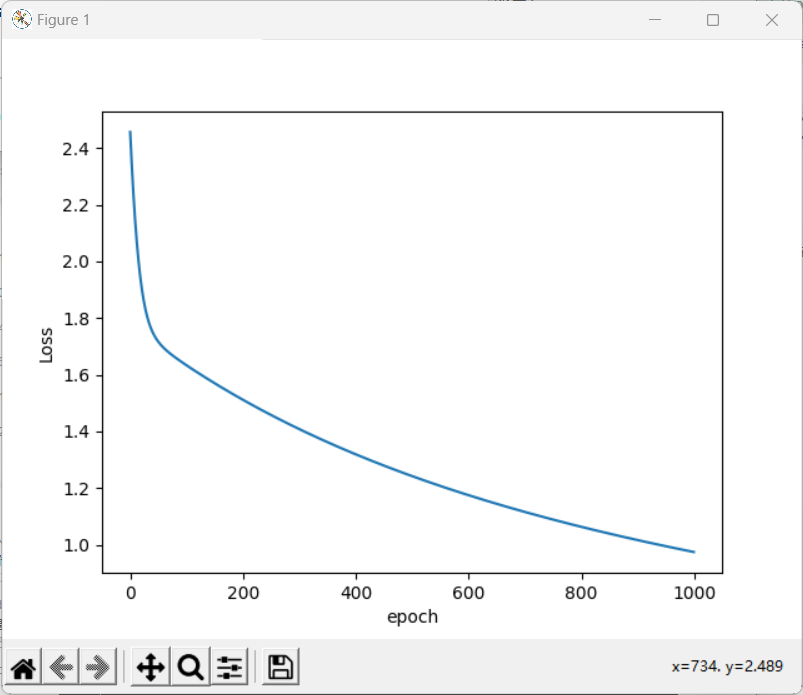
plt.plot(epoch_list,loss_list)

plt.ylabel('Loss')
plt.xlabel('epoch')
plt.show()

七、处理多维特征的输入 - Multiple Dimension lnput

引例：糖尿病数据集分类任务

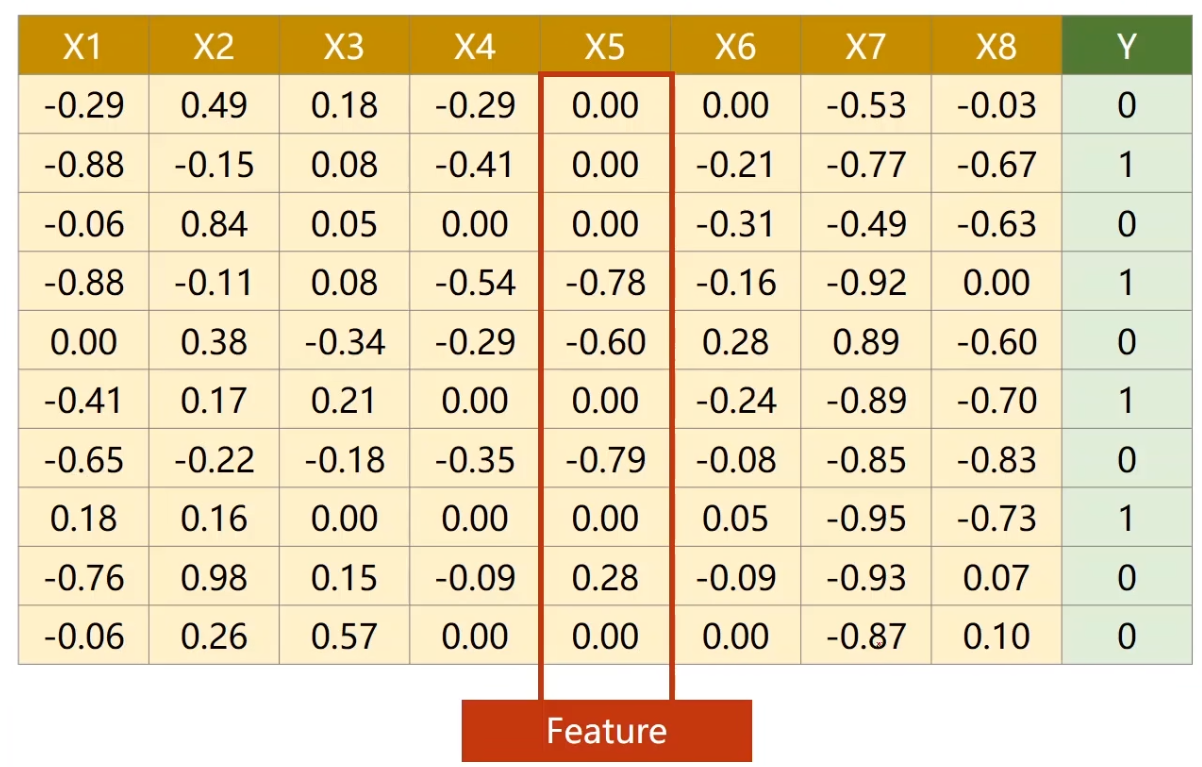
行称为：样本(Sample) 数据库中称为：记录(record)

列称为：特征数据库中称为：字段

注：sklearn中提供一个关于糖尿病的数据集可作为回归任务的数据集

Mlultiple Dimension Loqistic Regression Model

x可以看成一个向量，每一个x都要和w进行相乘，我们就可以写成图中上面的红色部分，因为标量的转置还是他自身，为了方便演示我们可以写成转置的形式。

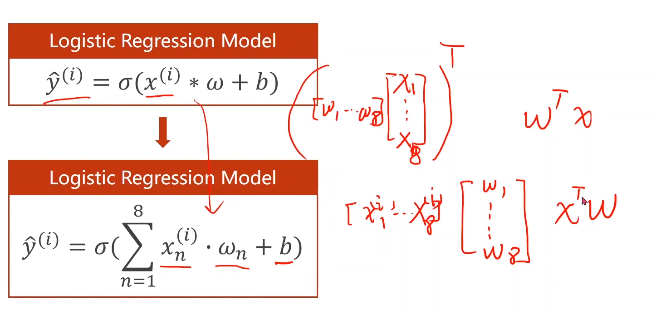
即：

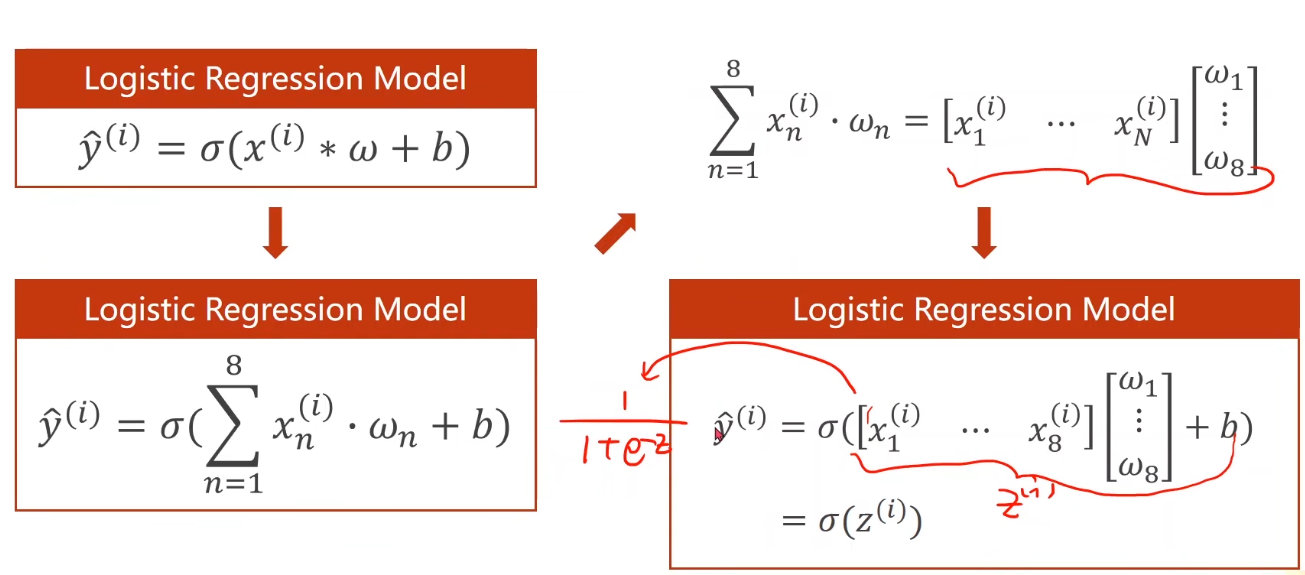
再来看下Mini-Batch(N samples)的情况

为什么这里要将方程运算转换成矩阵运算即向量形式呢？

———— 我们可以利用并行运算的能力，提高运行速度。

则只需将上一节的代码中数据准备和构建模型进行修改即可：

Logistics回归只有一层神经网络，若我们构造一个多层神经网络：

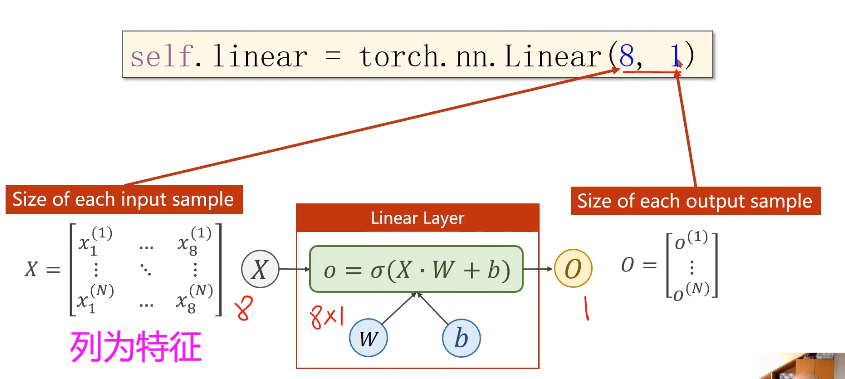
将矩阵看成一种空间变换的函数，这里的(8,2)是指将一个任意八维空间的向量映射到一个二维空间上，注意是线性的，而我们所做的空间变换不一定是线性的，

所以我们想要多个线性变换层通过找到最优的权重，把他们组合起来，来模拟一个非线性变换，

注意绿色框中我们引入的 $\sigma$ 即激活函数，在神经网络中我们通过引入激活函数给线性变换加入非线性操作，这样就使得我们可以去拟合相应的非线性变换。

对于本例我们使用 Example: Artificial Neural Network

1、建立数据集

import numpy as np
import torch

xy = np.loadtxt('./dataset/diabetes.csv.gz', delimiter=',', dtype=np.float32)
x_data = torch.from_numpy(xy[:, :-1])
y_data = torch.from_numpy(xy[:, [-1]])

分隔符为，
为什么用float32，因为常用游戏显卡只支持32位浮点数，只有特别贵的显卡才支持64位
由于课程中导入的数据是anaconda安装工具包中的自带的压缩文本数据，所以直接采用numpy中的loadtxt读取，这个函数可以直接读取Linux下压缩的格式，此处是.gz
因为我们的x和y是放在一起的所以：-1表示不要最后一列 → 拿出来前八列
注意y，所有行，拿出来需要加中括号，拿出来矩阵 → 拿出最后一列

2、模型建立

class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = torch.nn.Linear(8, 6)
        self.linear2 = torch.nn.Linear(6, 4)
        self.linear3 = torch.nn.Linear(4, 1)
        self.sigmoid = torch.nn.Sigmoid()

    def forward(self, x):
        x = self.sigmoid(self.linear1(x))
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        return x

model = Model()

注意上次调用的是nn.Function下的sigmoid，但是这里调用的是nn下的一个模块
forward函数中，如果是一串，就用一个x，上面的输出是下面的输入

3、构造损失函数和优化器

criterion = torch.nn.BCELoss(size_average=True)
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)

4、模型训练（虽然是mini-batch的风格但这里还是全部数据，下一节会涉及）

for epoch in range(100):
    # forward
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())

    # backword
    optimizer.zero_grad()
    loss.backward()

    # update
    optimizer.step()

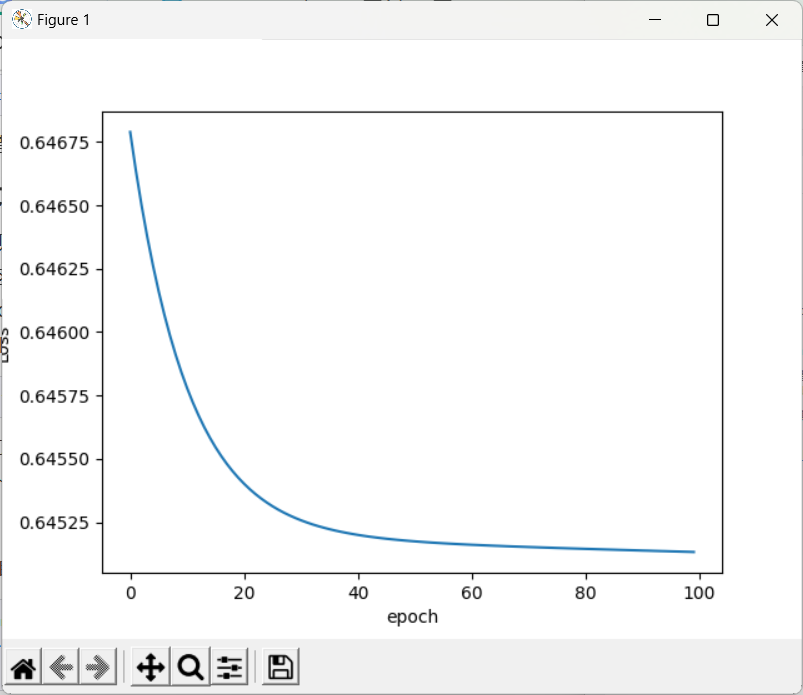
可以尝试不同的激活函数对结果的影响

torch.nn — PyTorch 2.1 documentation

Visualising Activation Functions in Neural Networks - dashee87.github.io

注意：Relu函数取值是0到1，如果最后的输入是小于0的，那么最后输出会是0，但我们可能会算In0，所以一般来说会将最后一层的激活函数改成sigmoid。

八、加载数据集 - Dataset and DataLoader

Dataset：加载数据集，支持我们以索引方式拿出样本
Dataloader：拿出一组Mini-Batch快速使用

三个概念：Epoch，Batch-size，Iterations

若使用Mini-Batch，我们的训练循环要写成嵌套循环
- - 外层循环：每一寸循环是一次epoch（训练周期）
  - 内层循环：每一次循环执行一个batch（对batch进行迭代）
Epoch：所有的样本都进行了一次训练
Batch-Size：每一次训练的样本数量
Iteration：Batch分了多少个，即内层迭代了多少次

Dataloader：分组，并做成可迭代的batch

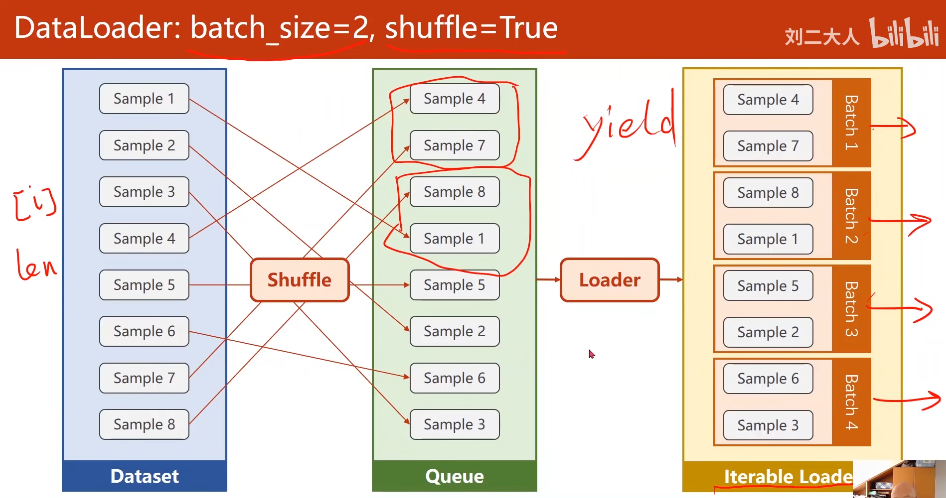
dataset抽象类不可实例化，dataloader可以实例化
数据集类里面有三个函数，这三个函数较为固定，分别自己的作用；
- 继承Dataset后我们必须实现三个函数：
  - __len__()帮助我们返回数据集大小
  - getitem__()帮助我们通过索引找到某个样本
  - __init__()是初始化函数，之后我们可以提供数据集路径进行数据的加载
Dataset的 init 中如果数据量较少可以导入所有的数据，若数据较大（图像、语音）无结构数据

import numpy as np
import torch
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt

epoch_list = []
loss_list = []

class DiabetesDataset(Dataset):
    def __init__(self,filepath):
        xy = np.loadtxt(filepath, delimiter=',', dtype=np.float32)
        self.len = xy.shape[0] #(n,9)
        self.x_data = torch.from_numpy(xy[:, :-1])
        self.y_data = torch.from_numpy(xy[:, [-1]])
    def __getitem__(self, index):
        return self.x_data[index],self.y_data[index]
    def __len__(self):
        return self.len

dataset = DiabetesDataset('D:\python_project\diabetes.csv.gz')
train_loader = DataLoader(dataset=dataset,batch_size=32,shuffle=True,num_workers=1)

class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = torch.nn.Linear(8, 6)
        self.linear2 = torch.nn.Linear(6, 4)
        self.linear3 = torch.nn.Linear(4, 1)
        self.sigmoid = torch.nn.Sigmoid()

    def forward(self, x):
        x = self.sigmoid(self.linear1(x))
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        return x

model = Model()

criterion = torch.nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

if __name__ == '__main__':
    for epoch in range(100):
        for i,data in enumerate(train_loader,0):
                print(1)
                # 1、准备数据
                inputs, labels = data
                # 2、前馈
                y_pred = model(inputs)
                loss = criterion(y_pred,labels)
                print(epoch,i,loss.item())
                # 3、反馈
                optimizer.zero_grad()
                loss.backward()
                # 4、更新
                optimizer.step()

                epoch_list.append(epoch)
                loss_list.append(loss.item())

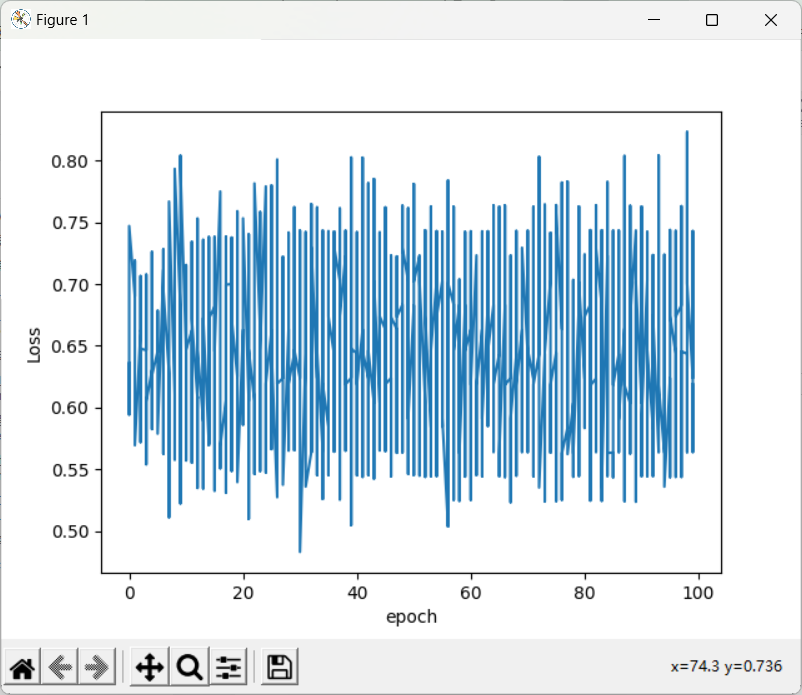
    plt.plot(epoch_list,loss_list)
    plt.ylabel('Loss')
    plt.xlabel('epoch')
    plt.show()

不是我结果怎这样？

更多数据集：

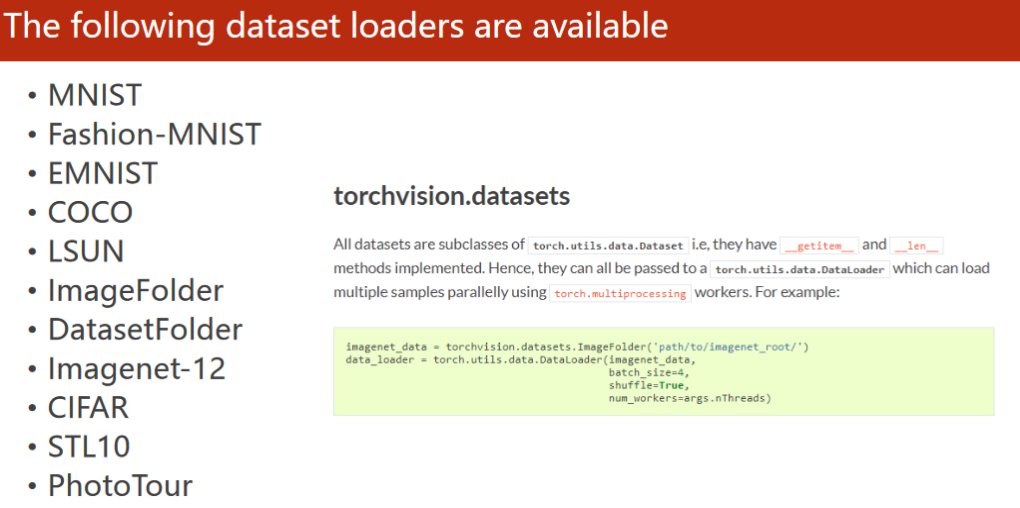
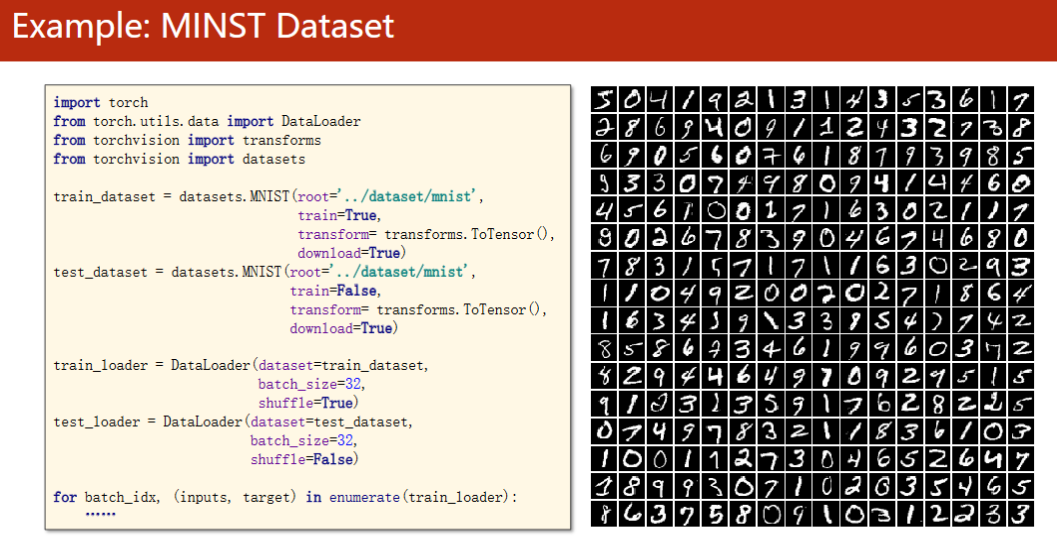
九、多分类问题 - Softmax分类器

Sigmoid函数主要用于解决二分类问题，它的特性在于将输入值映射到0和1之间的概率值。然而，在多类别问题中，我们需要将输入值映射到多个不同的类别上，而不仅仅是0和1。
如果我们尝试使用sigmoid函数来解决多类别问题，我们需要将其进行扩展以支持多个类别。一种常见的方法是使用一对多（One-vs-Rest）策略，其中针对每个类别训练一个独立的二分类模型。然后，我们可以使用sigmoid函数将每个模型的输出转换为概率值。
然而，这种方法存在一些问题。首先，由于每个模型都是独立训练的，可能会导致类别之间存在冲突或重叠。其次，sigmoid函数在处理极端情况时（接近0或1）容易饱和，这可能会导致梯度消失或梯度爆炸问题，对模型的训练造成困难。
因此，为了解决多类别问题，通常会使用其他适合的函数，如Softmax函数。Softmax函数可以将输入值映射到多个类别的概率分布，同时保持概率之和为1。这样，我们可以更好地处理多类别问题，并避免sigmoid函数的限制。

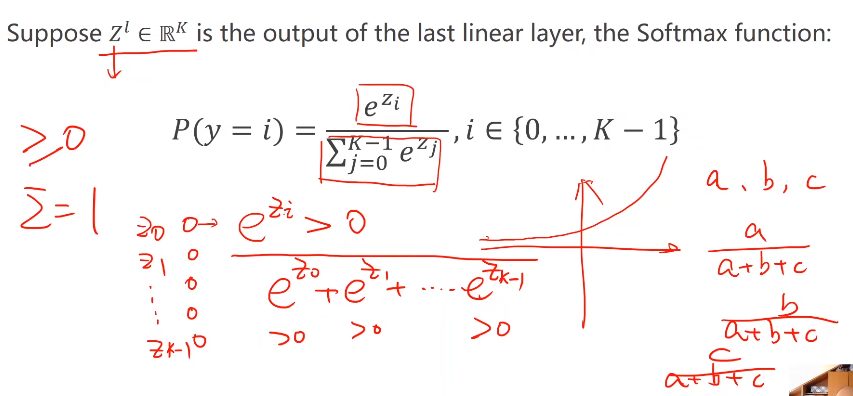
Softmax层：

因为只有一项结果会为0，所以在算Loss时只算一项即可。

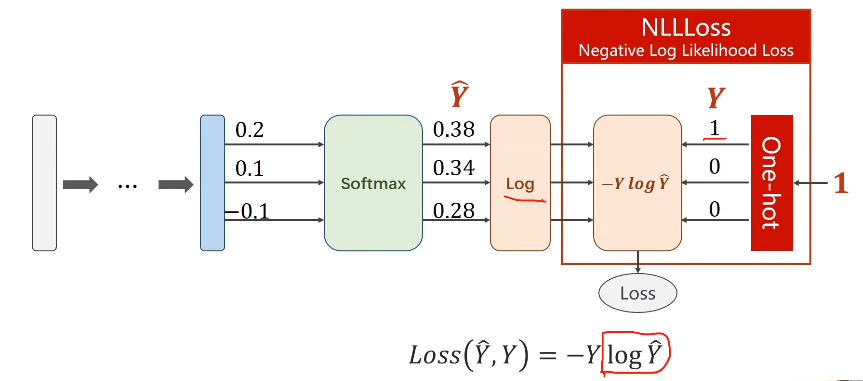
在pytorch中：

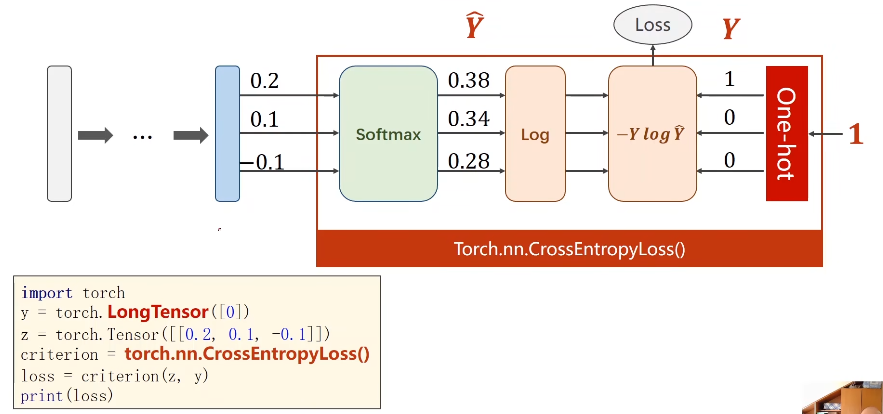
具体例子：

反看之前的题目：

lmplementation of classifier to MNIST dataset

ToTenser：神经网络想要的输入比较小，所以原始图像需要转变成一个图像张量
Normalize：标准化切换到 0,1 分布，参数为均值标准差，类似四六级成绩
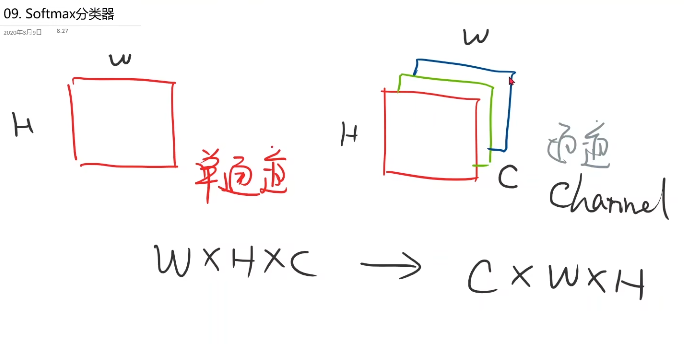
因为我们选用小批量，所以这里的N表示每个批量N个样本，每个样本都是一维28x28的图像
则输入为四阶张量，但在全连接神经网络中，要求输入必须是矩阵，
所以需要将1x28x28这个三阶张量变为一阶的向量
则只要将图像的每一行拼起来即可，一行即为784个元素，所以可以使用view函数，将输入变为二阶张量，第一个参数为-1，将来会自动算出对应值
最后得到 Nx784 的矩阵
注意：最后一层不做激活

• Reading the document:
• https://pytorch.org/docs/stable/nn.html#crossentropyloss
• https://pytorch.org/docs/stable/nn.html#nllloss
• Try to know why:
• CrossEntropyLoss <==> LogSoftmax + NLLLoss

部分文字参考于

【Pytorch深度学习实践】B站up刘二大人之SoftmaxClassifier-代码理解与实现(8/9)_softmax分类器代码-CSDN博客

视频及图片来源于

09.多分类问题_哔哩哔哩_bilibili