代码随想录算法训练营第二十七天 | LeetCode 93. 复原 IP 地址、78. 子集、90. 子集 II

文章链接：复原IP地址子集子集II

视频链接：复原IP地址子集子集II

1. LeetCode 93. 复原 IP 地址

1.1 思路

1.2 代码

2. LeetCode 78. 子集

2.1 思路

2.2 代码

3. LeetCode 90. 子集 II

3.1 思路

3.2 代码

1. LeetCode 93. 复原 IP 地址

1.1 思路

解释一下题目给出的一个“0”开头的合法 IP 地址，意思是如果是“0”开头了那这部分就只能是个 0，不能是“0235”这种。
首先定义个全局变量 result 里面放的是合法的字符串，是全部的答案
回溯函数的参数和返回值：返回值 void，参数首先是字符串 s，然后是 startIndex 是控制进入下一层递归时，从剩下的字符串中切割，就是告诉我们下一层递归从哪里开始切割，控制的是起始位置，再是 pointSum，因为我们要在字符串中加入 " . "，要加入才能放入 result 中，我们需要 3 个这个点。在代码中 startIndex 代表的就是我们的切割分割线，因为在我们进入下一层递归中时，startIndex 控制的就是从剩下的字符串中开始查找
终止条件：如果 pointSum==3，就要终止了，因为 IP 地址要三个点就行了，这个点就决定了树的深度，其实就是 3 层。这里注意下我们加入点的时候，是对加点位置的前面的字符串进行合法性判断，因为是 3 个点，但我们有 4 个子串，因此在终止条件中我们还需要对最后一段进行合法性判断，然后才能加入到 result 中。合法性判断的函数是 isValid。由上面的 startIndex 表示切割线的位置说明，isValid(s，startIndex，s.length()-1)，分别表示字符串，起始位置，终止位置，如果为 true 就加入到 result 中，然后 return 就行
单层搜索的逻辑：for(int i=startIndex;i<s.length();i++)，这个 for循环就是我们取数然后分割的过程，就要进行合法性判断，如果不合法就没必要往下遍历了。因此 if(isValid(s, startIndex, i))，其中 [startIndex, i] 这个就是子串的区间，本层中 startIndex 是固定的，但 i 是不断后移的，因此没毛病。如果合法，要先加入点，s=substring(start, i+1)+"."+substring(i+1) ，这里的 substring 函数是左闭右开的区间，因此要加 1，如果只传入一个参数就是这个位置往后的元素都要取出，然后 pointSum++。接着就向下一层递归 backtracking(s, i+2, pointSum)，这里为什么是加 2 而不是加 1，因为我们加了个点了，所以要跳 2 个位置。然后就是回溯，我们要把之前插入的点删去，s=s.substring(0, i+1)+substring(i+2)，这里就是跳过了那个点，然后 pointSum--，因为我们要继续往右搜索，因此加入的点要删去才能去右搜索
合法性判断：返回值 boolean，参数字符串 s，起始位置 start，结束位置 end，如果 start＞end 就 false；如果第一个位置是字符 '0'并且这个第一个位置不是终止位置，就 false；然后进入循环遍历，for(int i=start; i<=end; i++)这里要<=，因为 end 就是最后一个位置。然后如果字符串的 i 位置是>9 或者<0 的字符就 false，其实就是判断是否为 0 到 9 的数字；然后求整个子串是否在 0 到 255 之间，就 num=num*10+(s.charAt(i)-'0')，如果 num>255 就 false。以上均不发生就为 true。
提一下 s.charAt(i)-'0' 这步，其实就是字符的 ASCII 码值相减，比如是字符 ‘1’-‘0’，那么得到的结果就是真正的数字 1，字符 '0' 的 ASCII 码值是 48，字符 '1' 则是 49。

1.2 代码

//
class Solution {
    List<String> result = new ArrayList<>();

    public List<String> restoreIpAddresses(String s) {
        if (s.length() > 12) return result; // 算是剪枝了
        backTrack(s, 0, 0);
        return result;
    }

    // startIndex: 搜索的起始位置， pointNum:添加逗点的数量
    private void backTrack(String s, int startIndex, int pointNum) {
        if (pointNum == 3) {// 逗点数量为3时，分隔结束
            // 判断第四段⼦字符串是否合法，如果合法就放进result中
            if (isValid(s,startIndex,s.length()-1)) {
                result.add(s);
            }
            return;
        }
        for (int i = startIndex; i < s.length(); i++) {
            if (isValid(s, startIndex, i)) {
                s = s.substring(0, i + 1) + "." + s.substring(i + 1);    //在str的后⾯插⼊⼀个逗点
                pointNum++;
                backTrack(s, i + 2, pointNum);// 插⼊逗点之后下⼀个⼦串的起始位置为i+2
                pointNum--;// 回溯
                s = s.substring(0, i + 1) + s.substring(i + 2);// 回溯删掉逗点
            } else {
                break;
            }
        }
    }

    // 判断字符串s在左闭⼜闭区间[start, end]所组成的数字是否合法
    private Boolean isValid(String s, int start, int end) {
        if (start > end) {
            return false;
        }
        if (s.charAt(start) == '0' && start != end) { // 0开头的数字不合法
            return false;
        }
        int num = 0;
        for (int i = start; i <= end; i++) {
            if (s.charAt(i) > '9' || s.charAt(i) < '0') { // 遇到⾮数字字符不合法
                return false;
            }
            num = num * 10 + (s.charAt(i) - '0');
            if (num > 255) { // 如果⼤于255了不合法
                return false;
            }
        }
        return true;
    }
}

2. LeetCode 78. 子集

2.1 思路

这题要求的是集合里的所有子集，就是像数学集合里的一样，有 3 个元素，那就有 2^3 = 8 个子集。而且这里求的是组合，[1,2] 和 [2,1] 是一样的，所以本题依然要用 startIndex 来控制收集剩余集合时的起始位置。这题和上面的题区别在于收获结果的地方是很大差别的
这题比较大的区别就在于我们是要收集每个节点的结果，这个节点就是一层递归，每进入一层递归就把当前本层递归的单个结果放入 result 中
定义两个全局变量，result 放全部结果，path 放单个结果
回溯函数的参数和返回值：返回值 void，参数 nums，startIndex 来控制当前这个递归层从哪里开始往后取，也就是控制起始位置
终止条件：如果 startIndex>=nums.length 就是到了叶子节点的位置了，就 return
单层搜索的逻辑：for(int i= startIndex; i<nums.length; i++)，然后 path.add(nums[i])，然后就是递归的过程，backtracking(nums, i+1)，然后是回溯的过程，path.removeLast()去掉最后的元素然后继续往右搜索。
而我们收获结果的地方就是在这个回溯函数的第一行，就直接 result.add(path) 这样子，为什么放这里？因为我们递归进入时就要把当前的 path 放入 result 里，如果放在了终止条件下，那最后一个元素放入后进入递归就直接 return 了，就少了最后一个 path 子集

2.2 代码

//
class Solution {
    List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
    LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果
    public List<List<Integer>> subsets(int[] nums) {
        subsetsHelper(nums, 0);
        return result;
    }

    private void subsetsHelper(int[] nums, int startIndex){
        result.add(new ArrayList<>(path));//「遍历这个树的时候，把所有节点都记录下来，就是要求的子集集合」。
        if (startIndex >= nums.length){ //终止条件可不加
            return;
        }
        for (int i = startIndex; i < nums.length; i++){
            path.add(nums[i]);
            subsetsHelper(nums, i + 1);
            path.removeLast();
        }
    }
}

3. LeetCode 90. 子集 II

3.1 思路

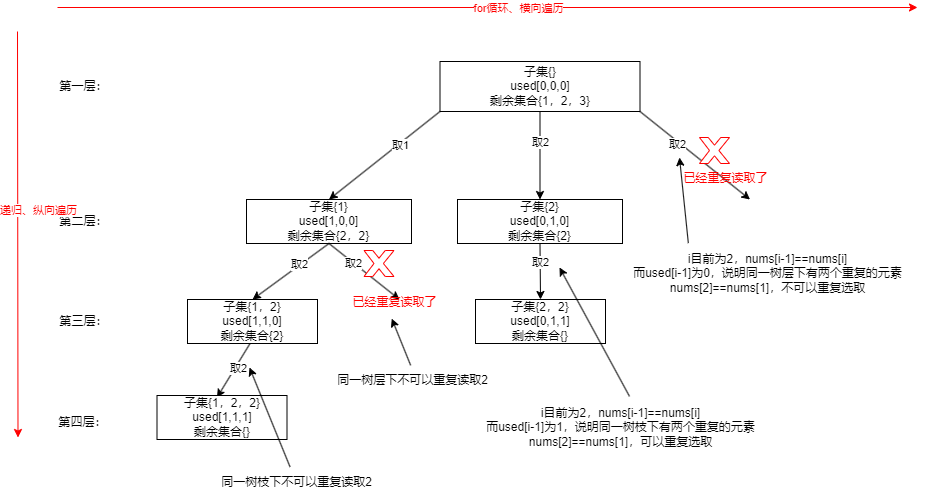
这集给的数组的元素是有重复元素的，这是和上题的区别，而且要求不能有重复子集，例如是不能出现 2 次 [1,2]。本题是结合了40. 组合总和 II和78. 子集。这题需要对回溯算法进行去重操作
我们需要一个 used 数组来标记哪个元素我们是否用过，true 为用过。我们用这种去重的操作方式需要先给题目的 nums 数组排序，因为我们要让相邻的元素挨在一起，因为这题同理要做的是树层去重。而且我们需要用 startIndex 来控制我们要在剩下的元素里取数，不然就会出现 [1,2]，[2,1] 这种情况。而树枝上不用去重，因为我们已经用了 startIndex 控制了起始位置，用的元素其实不是同一个元素，如果相同其实只是数值相同。而我们的树形结构上的所有节点都是我们的结果，也就决定了把 path 加入 result 的位置是放在回溯函数的首行。回溯函数进去后的时候就是一个节点，取数的过程是在 for循环里
定义全局变量 result 全部结果、path 单个结果、used 标记是否用过
回溯函数的参数和返回值：返回值 void，参数是 nums 数组，startIndex 控制起始位置
终止条件：startIndex>=nums.length 就 return
单层搜索的逻辑：首行先 result.add(path)，因为我们进入回溯函数后就证明这个节点已经是取好数的了。取数的过程就是 for(int i=startIndex; i<nums.length; i++)我们剪枝的过程是放在 for循环开始的，如果(i>0&&nums[i-1]==nums[i]&&!used[i-1])避免i-1为负数，首先要求i>0，然后是如果前后两个元素相等了就不能再取了，不然就重复了，然后下一个条件是前一个元素不能用过，这里是为了往下递归时，举例，取了一个1后，还能取多个1，这里的多个1不是同一个1，只是数值相同，这个条件不是为了树层去重的，而是为了取数找到结果。如果符合条件就是发现重复了就continue跳过此次循环，继续往后取。
然后就是继续收集元素的过程path.add(数组[i])；used[i]=true；然后就递归的过程backtracking(nums, i+1)。然后就是回溯的过程，path.removeLast()去除最后一个元素也就是刚刚加入的元素，这样才能往树的右边搜索，used[i]=false。这里又变为false是为了往右搜索，逻辑和第一层往右搜索的原因是一样的

3.2 代码

//
class Solution {
   List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
   LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果
   boolean[] used;
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        if (nums.length == 0){
            result.add(path);
            return result;
        }
        Arrays.sort(nums);
        used = new boolean[nums.length];
        subsetsWithDupHelper(nums, 0);
        return result;
    }
    
    private void subsetsWithDupHelper(int[] nums, int startIndex){
        result.add(new ArrayList<>(path));
        if (startIndex >= nums.length){
            return;
        }
        for (int i = startIndex; i < nums.length; i++){
            if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]){
                continue;
            }
            path.add(nums[i]);
            used[i] = true;
            subsetsWithDupHelper(nums, i + 1);
            path.removeLast();
            used[i] = false;
        }
    }
}