1、简介
泰勒公式,也称泰勒展开式。是用一个函数在某点的信息,描述其附近取值的公式。如果函数足够平滑,在已知函数在某一点的各阶导数值的情况下,泰勒公式可以利用这些导数值来做系数,构建一个多项式近似函数,求得在这一点的邻域中的值,
所以泰勒公式是做什么用的?
简单来讲就是用一个多项式函数去逼近一个给定的函数(即尽量使多项式函数图像拟合给定的函数图像),注意,逼近的时候一定是从函数图像上的某个点展开。如果一个非常复杂函数,想求其某点的值,直接求无法实现,这时候可以使用泰勒公式去近似的求该值,这是泰勒公式的应用之一。泰勒公式在机器学习中主要应用于梯度迭代。
2、近似计算举例
初等数学已经了解到一些函数如:![]() 的一些重要性质,但是初等数学不曾回答怎样来计算它们,以
的一些重要性质,但是初等数学不曾回答怎样来计算它们,以 的近似计算为例:
2.1 重访线性化
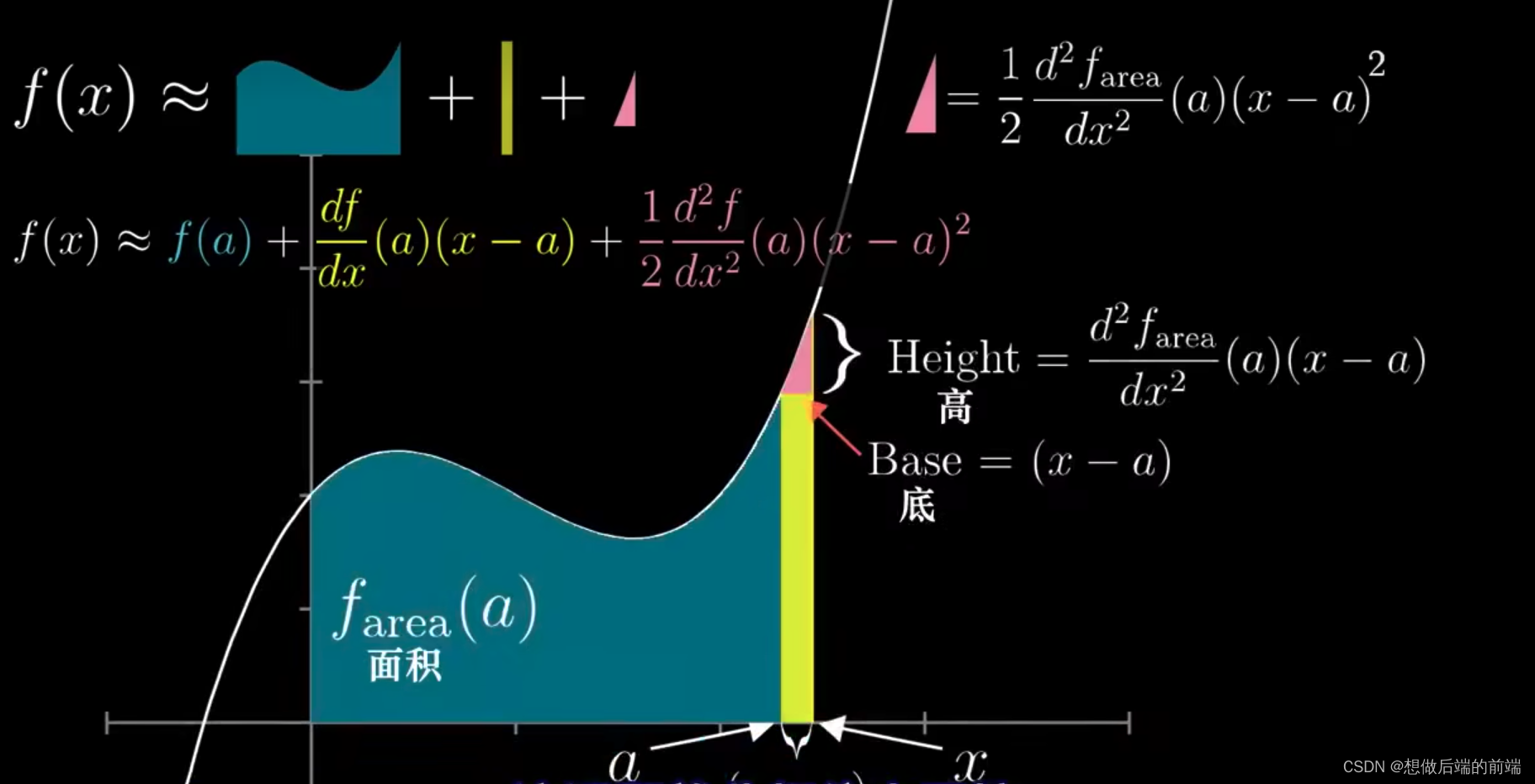
在点 (a,f(a)) 附近,与曲线y = f(x) 最近似的直线方程是什么?答案是所求直线为曲线上点 (a,f(a))处的切线,他的方程为: 这就是 f 在 x = a 的线性化,右边是次数为1的多项式,下图给出了曲线
在
的切线,看起来不像是整个曲线的近似
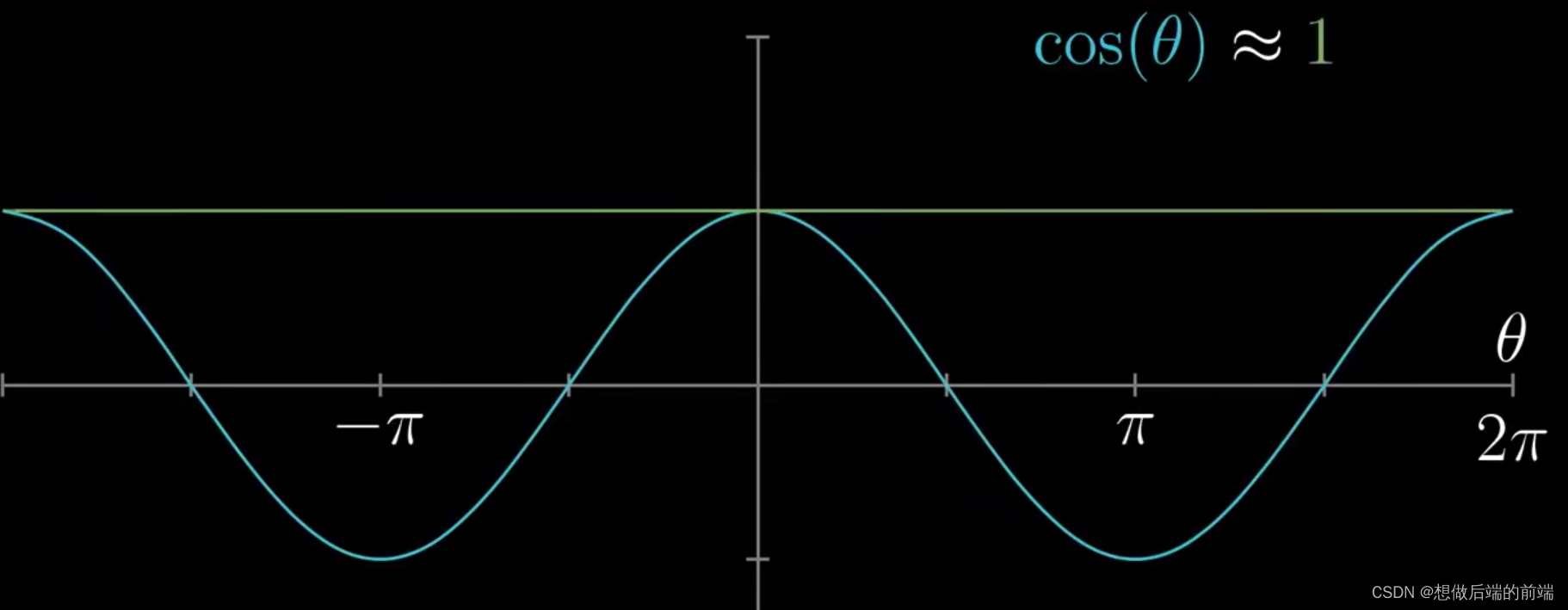
2.2 二阶近似
为什么只讨论直线那?我们来看看抛物线:在点 (a,f(a)) 附近,与曲线y = f(x) 最近似的二次曲线方程是什么?采用相同的函数,下图是二次曲线可能的样子。
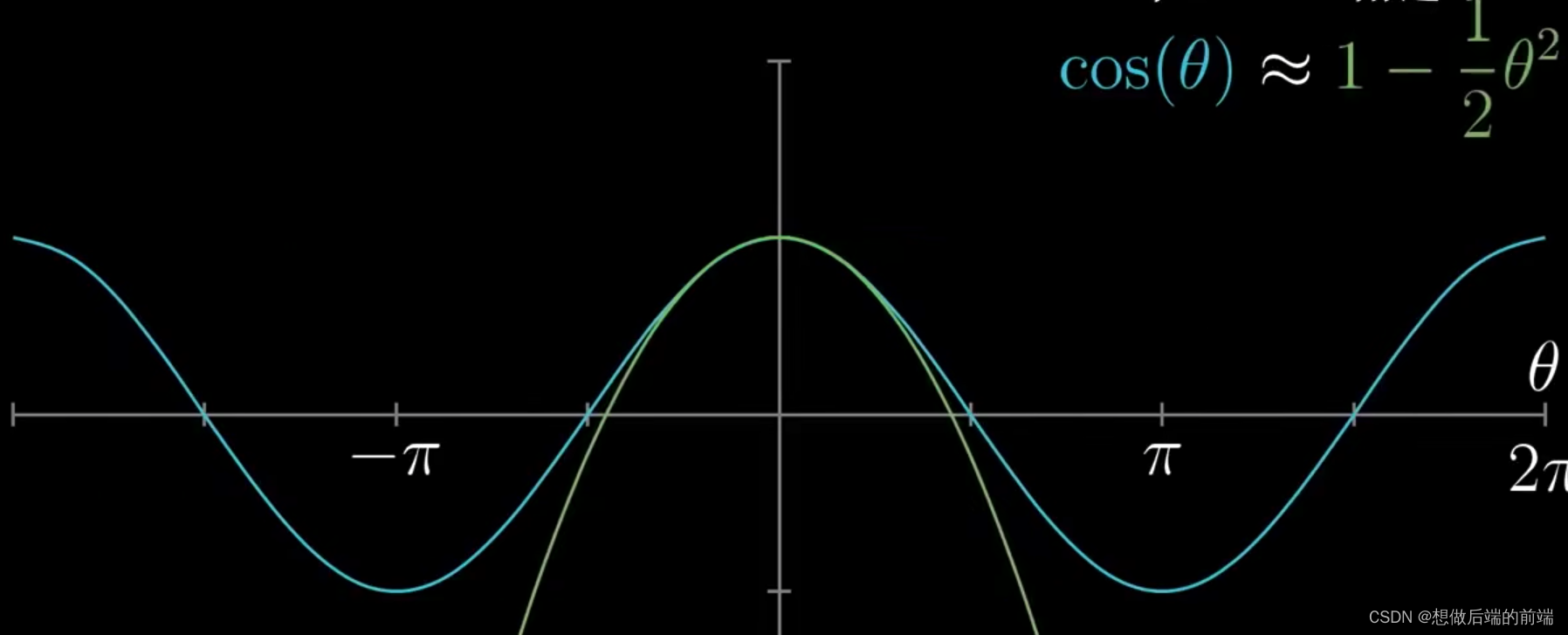
事实上,在x接近于a时,最近似于曲线的二次曲线方程为:
他其实是一个关于x的二次函数,因为若,展开,则x的最高次项为
,这里仍保留了相同的形式,我们称该二次函数为
即:
2.3 高阶近似
我们继续以相同形式讨论,只不过这里的用任意次N代替1或2.问题:对于a附近的x那个次数为N或更低的多项式最近似f(x)?答案由下面的定理给出。
在这里大家可能会有很多疑问,比如为什么每次要除以N!,这是因为在每多求一次导数,就会有一个N乘,所以要除去这个影响。
3、 泰勒公式的定义
所以我们就得到了泰勒公式的定义:
如果函数 f(x)在含 x0的某个开区间 (a,b)内具有直到 (n+1) 阶导数,则对 ∀x∈(a,b),有
其中余项 (即误差) , ξ 在 x0 与 x 之间。泰勒公式的余项表达方式有好几种,前面这种表是方法称为n阶泰勒展开式的拉格朗日余项。拉格朗日余项即是n阶泰勒公式又多展开了一阶,n变为n+1。注意,这里的余项即为误差,因为使用多项式函数在某点展开,逼近给定函数,最后肯定会有一丢丢的误差,我们称之为余项。
4、扩展 —— 麦克劳林公式
是泰勒公式的一种特殊情况:即当 x0=0 时的泰勒公式。所以将 x0=0 带入公式,即得:
几个常见的初等函数的带有佩亚诺余项的麦克劳林公式:
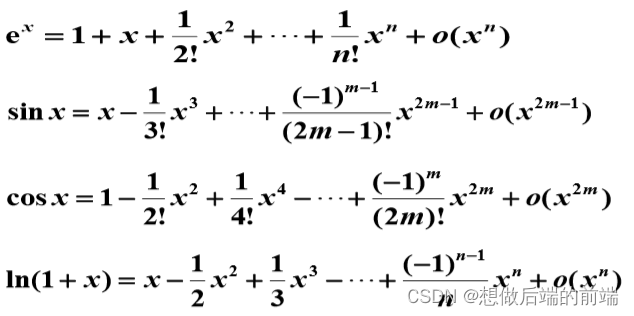


![2023年全球线上教育营收规模及未来发展趋势分析:推动知识付费市场增长[图]](https://img-blog.csdnimg.cn/img_convert/83d7ab1992680c3e8794acbd8e2f2bed.png)